贵州省高考数学模拟试卷与解析(文科)

这是一份贵州省高考数学模拟试卷与解析(文科)，共17页。试卷主要包含了选择题，填空题，简答题等内容，欢迎下载使用。
贵州省高考数学模拟试卷（文科）　
一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知集合A={x|x=2k﹣1，k∈Z}，B={﹣1，0，1，2，3，4}，则集合A∩B中元素的个数为（　　）
A．1 B．2 C．3 D．4
2．已知复数z满足（z﹣2）i=1+i（i是虚数单位），则z=（　　）
A．3﹣i B．﹣3+i C．﹣3﹣i D．3+i
3．在等差数列{an}中，a3﹣a2=﹣2，a7=﹣2，则a9=（　　）
A．2 B．﹣2 C．﹣4 D．﹣6
4．某工厂生产A、B、C三种不同型号的产品，其数量之比依次是3：4：7，现在用分层抽样的方法抽出样本容量为n的样本，样本中A型号产品有15件，那么n等于（　　）
A．50 B．60 C．70 D．80
5．不等式组所表示的平面区域的面积为（　　）
A．1 B．2 C．3 D．4
6．一个几何体的三视图如图所示，其中正视图是正三角形，则该几何体的体积为（　　）
A． B．8 C． D．
7．设α、β是两个不重合的平面，m、n是两条不重合的直线，则以下结论错误的是（　　）
A．若α∥β，m⊂α，则 m∥β B．若m∥α，m∥β，α∩β=n，则 m∥n
C．若m⊂α，n⊂α，m∥β，n∥β，则α∥β D．若m∥α，m⊥β，则α⊥β
8．已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4，则实数a的值是（　　）
A．﹣2 B．﹣4 C．﹣6 D．﹣8
9．阅读如图所示的程序框图，若输出的结果是63，则判断框内n的值可为（　　）

A．8 B．7 C．6 D．5
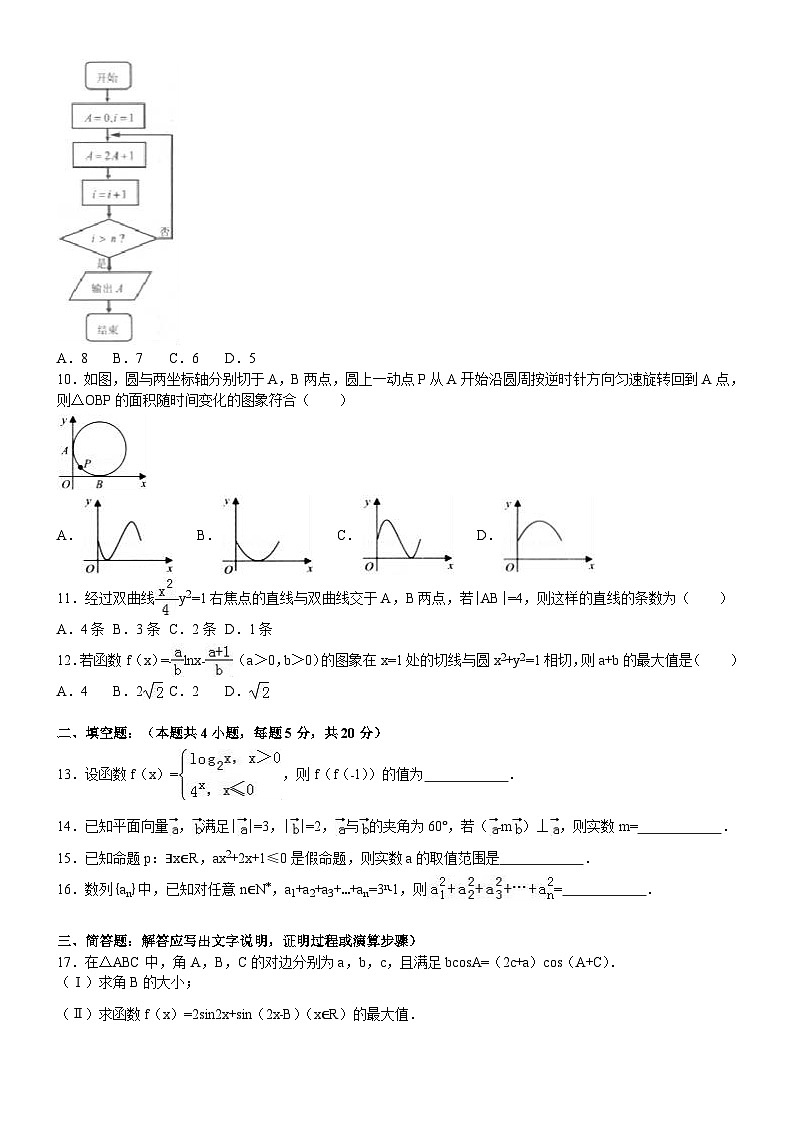
10．如图，圆与两坐标轴分别切于A，B两点，圆上一动点P从A开始沿圆周按逆时针方向匀速旋转回到A点，则△OBP的面积随时间变化的图象符合（　　）

A． B． C． D．
11．经过双曲线﹣y2=1右焦点的直线与双曲线交于A，B两点，若|AB|=4，则这样的直线的条数为（　　）
A．4条 B．3条 C．2条 D．1条
12．若函数f（x）=﹣lnx﹣（a＞0，b＞0）的图象在x=1处的切线与圆x2+y2=1相切，则a+b的最大值是（　　）
A．4 B．2 C．2 D．
　
二、填空题：（本题共4小题，每题5分，共20分）
13．设函数f（x）=，则f（f（﹣1））的值为　　　　　　．
14．已知平面向量，满足||=3，||=2，与的夹角为60°，若（﹣m）⊥，则实数m=　　　　　　．
15．已知命题p：∃x∈R，ax2+2x+1≤0是假命题，则实数a的取值范围是　　　　　　．
16．数列{an}中，已知对任意n∈N*，a1+a2+a3+…+an=3n﹣1，则=　　　　　　．
　
三、简答题：解答应写出文字说明，证明过程或演算步骤）
17．在△ABC中，角A，B，C的对边分别为a，b，c，且满足bcosA=（2c+a）cos（A+C）．
（Ⅰ）求角B的大小；
（Ⅱ）求函数f（x）=2sin2x+sin（2x﹣B）（x∈R）的最大值．
18．如图1，在直角梯形ABCD中，∠ADC=90°，CD∥AB，AD=CD=AB=2．将△ADC沿AC折起，使平面ADC⊥平面ABC，得到如图2所示的几何体D﹣ABC
（Ⅰ）求证：AD⊥平面BCD；
（Ⅱ）求点C到平面ABD的距离．

19．在某次考试中，全部考生参加了“科目一”和“科目二”两个科目的考试，每科成绩分为A，B，C，D，E五个等级．某考场考生的两科考试成绩数据统计如图所示，其中“科目一”成绩为D的考生恰有4人．

（1）分别求该考场的考生中“科目一”和“科目二”成绩为A的考生人数；
（2）已知在该考场的考生中，恰有2人的两科成绩均为A，在至少一科成绩为A的考生中，随机抽取2人进行访谈，求这2人的两科成绩均为A的概率．
20．设椭圆C： +=1（a＞b＞0）的左、右焦点分别为F1，F2，上顶点为A，过点A与AF2垂直的直线交x轴负半轴于点Q，且F1恰是QF2的中点．若过A、Q、F2三点的圆恰好与直线l：x﹣y﹣3=0相切．
（1）求椭圆C的方程；
（2）设直线l1：y=x+2与椭圆C交于G、H两点．在x轴上是否存在点P（m，0），使得以PG，PH为邻边的平行四边形是菱形．如果存在，求出m的取值范围，如果不存在，请说明理由．

21．已知函数f（x）=x2﹣mlnx，g（x）=x2﹣2x，F（x）=f（x）﹣g（x）
（Ⅰ）当m＞0，求函数f（x）的单调区间；
（Ⅱ）当m=﹣1时，试问过点（2，5）可作多少条直线与曲线y=F（x）相切？说明理由．
　
请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-1：几何证明选讲]
22．已知BC为圆O的直径，点A为圆周上一点，AD⊥BC于点D，过点A作圆O的切线交BC的延长线于点P，过点B作BE垂直PA的延长线于点E．求证：
（1）PA•PD=PE•PC；
（2）AD=AE．

　
[选修4-4：坐标系与参数方程]
23．已知直线l的参数方程为（t为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=4cos（θ﹣）
（Ⅰ）求曲线C的直角坐标方程；
（Ⅱ）若点P（x，y）是直线l上位于圆内的动点（含端点），求x+y的最大值和最小值．
　
[选修4-5：不等式选讲]．
24．已知函数f（x）=m﹣|x﹣2|（m＞0），且f（x+2）≥0的解集为[﹣3，3]
（Ⅰ）求m的值；
（Ⅱ）若a＞0，b＞0，c＞0且++=，求证：2a+3b+4c≥9．
　
贵州省高考数学模拟试卷（文科）试题解析
一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知集合A={x|x=2k﹣1，k∈Z}，B={﹣1，0，1，2，3，4}，则集合A∩B中元素的个数为（　　）
A．1 B．2 C．3 D．4
【考点】交集及其运算．
【分析】列举出A中的元素，求出两集合的交集，即可作出判断．
【解答】解：∵A={x|x=2k﹣1，k∈Z}={…，﹣3，﹣1，1，3，5，…}，B={﹣1，0，1，2，3，4}，
∴A∩B={﹣1，1，3}，
则集合A∩B中元素的个数为3，
故选：C．
　
2．已知复数z满足（z﹣2）i=1+i（i是虚数单位），则z=（　　）
A．3﹣i B．﹣3+i C．﹣3﹣i D．3+i
【考点】复数代数形式的乘除运算．
【分析】把已知等式变形，然后利用复数代数形式的乘除运算化简得答案．
【解答】解：由（z﹣2）i=1+i，得
，
∴z=3﹣i．
故选：A．
　
3．在等差数列{an}中，a3﹣a2=﹣2，a7=﹣2，则a9=（　　）
A．2 B．﹣2 C．﹣4 D．﹣6
【考点】等差数列的通项公式．
【分析】由a3﹣a2=﹣2，即d=﹣2，再根据等差数列的性质即可求出．
【解答】解：由a3﹣a2=﹣2，即d=﹣2，
∴a9=a7+2d=﹣2+2×（﹣2）=﹣6，
故选：D．
　
4．某工厂生产A、B、C三种不同型号的产品，其数量之比依次是3：4：7，现在用分层抽样的方法抽出样本容量为n的样本，样本中A型号产品有15件，那么n等于（　　）
A．50 B．60 C．70 D．80
【考点】分层抽样方法．
【分析】根据分层抽样的定义和方法，可得=，由此求得n的值．
【解答】解：根据分层抽样的定义和方法，可得=，
解得n=70，
故选：C．
　
5．不等式组所表示的平面区域的面积为（　　）
A．1 B．2 C．3 D．4
【考点】简单线性规划．
【分析】作出不等式对应的平面区域，根据平面区域的形状确定平面区域的面积．
【解答】解：不等式组对应的平面区域如图：
则对应区域为直角三角形ABC．
则三点坐标分别为A（2，3），B（4，3），C（4，5），
则AB=2，BC=2，
所以三角形的面积为S=×2×2=2．
故选：B．

　
6．一个几何体的三视图如图所示，其中正视图是正三角形，则该几何体的体积为（　　）
A． B．8 C． D．
【考点】由三视图求面积、体积．
【分析】由三视图知该几何体是一个三棱锥，由三视图求出几何元素的长度，由锥体的体积公式求出几何体的体积．
【解答】解：根据三视图可知几何体是一个三棱锥，
由俯视图知，底面是一个等腰三角形，底和底边上高分别是4、2，
∵正视图是正三角形，∴三棱锥的高是，
∴几何体的体积V==，
故选：C．
　
7．设α、β是两个不重合的平面，m、n是两条不重合的直线，则以下结论错误的是（　　）
A．若α∥β，m⊂α，则 m∥β B．若m∥α，m∥β，α∩β=n，则 m∥n
C．若m⊂α，n⊂α，m∥β，n∥β，则α∥β D．若m∥α，m⊥β，则α⊥β
【考点】空间中直线与平面之间的位置关系．
【分析】若α∥β，m⊂α，根据面面平行的性质，可得m∥β；
若m∥α，m∥β，α∩β=n，根据线面平行的性质，可得m∥n；
若“m⊂α，n⊂α，m∥β，n∥β，且m∩n=O”，则“α∥β”成立，但条件中缺少了“m∩n=O”，故结论“α∥β”不一定成立；
若m∥α，经过m的平面与α相交于a，则可得m中m∥a，由于m⊥β，所以a⊥β，根据面面垂直的判定定理，可得α⊥β．
【解答】解：若α∥β，m⊂α，根据面面平行的性质，可得m∥β，故A正确；
若m∥α，m∥β，α∩β=n，根据线面平行的性质，可得m∥n，故B正确；
若“m⊂α，n⊂α，m∥β，n∥β，且m∩n=O”，则“α∥β”成立，但条件中缺少了“m∩n=O”，故结论“α∥β”不一定成立，得C错误；
若m∥α，经过m的平面与α相交于a，则可得m中m∥a，由于m⊥β，所以a⊥β，根据面面垂直的判定定理，可得α⊥β，故D正确．
故选：C．
　
8．已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4，则实数a的值是（　　）
A．﹣2 B．﹣4 C．﹣6 D．﹣8
【考点】直线与圆的位置关系．
【分析】把圆的方程化为标准形式，求出弦心距，再由条件根据弦长公式求得a的值．
【解答】解：圆x2+y2+2x﹣2y+a=0 即 （x+1）2+（y﹣1）2=2﹣a，
故弦心距d==．
再由弦长公式可得 2﹣a=2+4，∴a=﹣4，
故选：B．
　
9．阅读如图所示的程序框图，若输出的结果是63，则判断框内n的值可为（　　）

A．8 B．7 C．6 D．5
【考点】程序框图．
【分析】由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量A的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．
【解答】解：第一次执行循环体后，A=1，i=2，不满足退出循环的条件；
第二次执行循环体后，A=3，i=3，不满足退出循环的条件；
第三次执行循环体后，A=7，i=4，不满足退出循环的条件；
第四次执行循环体后，A=15，i=5，不满足退出循环的条件；
第五次执行循环体后，A=31，i=6，不满足退出循环的条件；
第六次执行循环体后，A=63，i=7，满足退出循环的条件；
故退出循环的条件应为：i＞6，
故选：C
　
10．如图，圆与两坐标轴分别切于A，B两点，圆上一动点P从A开始沿圆周按逆时针方向匀速旋转回到A点，则△OBP的面积随时间变化的图象符合（　　）

A． B． C． D．
【考点】函数的图象．
【分析】分类讨论，结核函数值的变化情况以及所给的选项，得出结论．
【解答】解：当点P从A运动到B的过程中，△OBP的面积逐渐减小，在点B处，△OBP的面积为零．
当点P从B运动到圆的最高点的过程中，△OBP的面积又逐渐增大，
且当P位于圆的最高点时，△OBP的面积达到最大值．
当点P从最高点运动到A的过程中，△OBP的面积又逐渐减小，
故选：A．
　
11．经过双曲线﹣y2=1右焦点的直线与双曲线交于A，B两点，若|AB|=4，则这样的直线的条数为（　　）
A．4条 B．3条 C．2条 D．1条
【考点】双曲线的简单性质．
【分析】根据题意，求得a、b的值，根据直线与双曲线相交的情形，分两种情况讨论：①AB只与双曲线右支相交，②AB与双曲线的两支都相交，分析其弦长的最小值，可得符合条件的直线的数目，综合可得答案．
【解答】解：由双曲线﹣y2=1，可得a=2，b=1．
若AB只与双曲线右支相交时，AB的最小距离是通径，
长度为=1，
∵AB=4＞1，∴此时有两条直线符合条件；
若AB与双曲线的两支都相交时，此时AB的最小距离是实轴两顶点的距离，
长度为2a=4，距离无最大值，
∵AB=4，∴此时有1条直线符合条件；
综合可得，有3条直线符合条件．
故选：B．
　
12．若函数f（x）=﹣lnx﹣（a＞0，b＞0）的图象在x=1处的切线与圆x2+y2=1相切，则a+b的最大值是（　　）
A．4 B．2 C．2 D．
【考点】利用导数研究曲线上某点切线方程；圆的切线方程．
【分析】求导数，求出切线方程，利用切线与圆x2+y2=1相切，可得a2+b2=1，利用基本不等式，可求a+b的最大值．
【解答】解：f（x）=﹣lnx﹣的导数为f′（x）=﹣•，
令x=1，可得切线的斜率为f′（1）=﹣，又f（1）=﹣，
则切线方程为y+=﹣（x﹣1），即ax+by+1=0，
∵切线与圆x2+y2=1相切，
∴=1，
∴a2+b2=1，
∵a＞0，b＞0
∴a2+b2≥2ab，
∴2（a2+b2）≥（a+b）2，
∴a+b≤=．
∴a+b的最大值是．
故选：D．
　
二、填空题：（本题共4小题，每题5分，共20分）
13．设函数f（x）=，则f（f（﹣1））的值为　﹣2　．
【考点】分段函数的应用；函数的值．
【分析】直接利用分段函数化简求解即可．
【解答】解：函数f（x）=，
则f（﹣1）=，
f（f（﹣1））=f（）=log2=﹣2．
故答案为：﹣2．
　
14．已知平面向量，满足||=3，||=2，与的夹角为60°，若（﹣m）⊥，则实数m=　3　．
【考点】数量积判断两个平面向量的垂直关系．
【分析】由题意可得=3×2×cos60°=3，（）•=﹣m=9﹣m×3=0，解方程求得实数m的值．
【解答】解：由题意可得=3×2×cos60°=3，（）•=﹣m=9﹣m×3=0，
∴m=3，
故答案为：3．
　
15．已知命题p：∃x∈R，ax2+2x+1≤0是假命题，则实数a的取值范围是　a＞1　．
【考点】特称命题；命题的真假判断与应用．
【分析】将条件转化为ax2+2x+1＞0恒成立，检验a=0是否满足条件，当a≠0 时，必须，从而解出实数a的取值范围．
【解答】解：命题p：∃x∈R，ax2+2x+1≤0是假命题，
即“ax2+2x+1＞0“是真命题 ①．
当a=0 时，①不成立，
当a≠0时，要使①成立，必须，解得a＞1，
故实数a的取值范围为a＞1．
故答案为：a＞1．
　
16．数列{an}中，已知对任意n∈N*，a1+a2+a3+…+an=3n﹣1，则=　　．
【考点】数列的求和．
【分析】设数列{an}的前n项和为Sn，则，当n≥2时，．即可得出an=Sn﹣Sn﹣1．进而得到，再利用等比数列的前n项和公式即可得出．
【解答】解：设数列{an}的前n项和为Sn，则，当n≥2时，．
∴an=Sn﹣Sn﹣1=3n﹣1﹣（3n﹣1﹣1）=2×3n﹣1，当n=1时也成立．
∴=（2×3n﹣1）2=4×9n﹣1．
∴=4（90+91+…+9n﹣1）==．
故答案为：．
　
三、简答题：解答应写出文字说明，证明过程或演算步骤）
17．在△ABC中，角A，B，C的对边分别为a，b，c，且满足bcosA=（2c+a）cos（A+C）．
（Ⅰ）求角B的大小；
（Ⅱ）求函数f（x）=2sin2x+sin（2x﹣B）（x∈R）的最大值．
【考点】正弦定理；三角函数的最值．
【分析】（Ⅰ）由正弦定理和和差角的三角函数公式可得cosB，可得角B；
（Ⅱ）由（Ⅰ）和三角函数公式化简可得f（x）=sin（2x﹣），易得函数最大值．
【解答】解：（Ⅰ）∵在△ABC中bcosA=（2c+a）cos（A+C），
∴由正弦定理可得sinBcosA=（2sinC+sinA）（﹣cosB），
∴sinBcosA+cosBsinA=﹣2sinCcosB，
∴sin（A+B）=﹣2sinCcosB，即sinC=﹣2sinCcosB，
约掉sinC可得cosB=﹣，B=；
（Ⅱ）由（Ⅰ）化简可得f（x）=2sin2x+sin（2x﹣）
=2sin2x+sin2xcos﹣cos2xsin
=2sin2x﹣sin2x﹣cos2x
=sin2x﹣cos2x=sin（2x﹣），
∴当2x﹣=2kπ+即x=kπ+，k∈Z时，函数取最大值．
　
18．如图1，在直角梯形ABCD中，∠ADC=90°，CD∥AB，AD=CD=AB=2．将△ADC沿AC折起，使平面ADC⊥平面ABC，得到如图2所示的几何体D﹣ABC
（Ⅰ）求证：AD⊥平面BCD；
（Ⅱ）求点C到平面ABD的距离．

【考点】点、线、面间的距离计算；直线与平面垂直的判定．
【分析】（I）由题意可得：AC=BC=2，又AB2=AC2+BC2，可得AC⊥CB，由面面垂直的性质定理可得：BC⊥平面ADC，可得BC⊥AD．又AD⊥DC，即可证明结论．
（II）由（I）可知：平面ABD⊥平面BCD．过点C作CH⊥BD，垂足为H．可得CH⊥平面ABD．利用CH=即可得出．
【解答】（I）证明：由题意可得：AC=BC=2，∴AB2=AC2+BC2，∴AC⊥CB，
又平面ADC⊥平面ABC，∴BC⊥平面ADC，∴BC⊥AD．
又AD⊥DC，DC∩BC=C，
∴AD⊥平面BCD．
（II）解：由（I）可知：平面ABD⊥平面BCD．过点C作CH⊥BD，垂足为H．则CH⊥平面ABD．CH为点C到平面ABD的距离．
∵BC⊥平面ADC，∴BC⊥CD．
在Rt△BCD中，BC=2，CD=2，∴BD==2．
∴CH===．
∴点C到平面ABD的距离是．

　
19．在某次考试中，全部考生参加了“科目一”和“科目二”两个科目的考试，每科成绩分为A，B，C，D，E五个等级．某考场考生的两科考试成绩数据统计如图所示，其中“科目一”成绩为D的考生恰有4人．

（1）分别求该考场的考生中“科目一”和“科目二”成绩为A的考生人数；
（2）已知在该考场的考生中，恰有2人的两科成绩均为A，在至少一科成绩为A的考生中，随机抽取2人进行访谈，求这2人的两科成绩均为A的概率．
【考点】列举法计算基本事件数及事件发生的概率．
【分析】（1）根据题意，求出考生人数，计算考生“科目一”和“科目二”成绩为A的考生人数即可．
（2）通过列举的方法计算出选出的2人所有可能的情况及这两人的两科成绩等级均为A的情况；利用古典概型概率公式求出随机抽取两人进行访谈，这两人的两科成绩等级均为A的概率．
【解答】解：（1）“考生中“科目一”科目中D等级学生所占的频率为1﹣0.2﹣0.375﹣0.25﹣0.075=0.1，
因为“科目一”科目中成绩为D的考生有4人，所以该考场共有4÷0.1=40（人）．
所以该考场学生中“科目一”科目成绩等级为A的人数为40×0.075=3人，
所以该考场学生中“科目二”科目成绩等级为A的人数为40×（1﹣0.375﹣0.375﹣0.15﹣0.025）=40×0.075=3（人）．
（2）因为两科考试中，共有6人得分等级为A，又恰有两人的两科成绩等级均为A，
所以还有2人只有一个科目得分为A，
设这四人为甲，乙，丙，丁，其中甲，乙是两科成绩都是A的同学，
则在至少一科成绩等级为A的考生中，随机抽取两人进行访谈，基本事件空间为：
Ω={{甲，乙}，{甲，丙}，{甲，丁}，{乙，丙}，{乙，丁}，{丙，丁}}，一共有6个基本事件．
设“随机抽取两人进行访谈，这两人的两科成绩等级均为A”为事件M，所以事件M中包含的基本事件有1个，
则P（M）=．
　
20．设椭圆C： +=1（a＞b＞0）的左、右焦点分别为F1，F2，上顶点为A，过点A与AF2垂直的直线交x轴负半轴于点Q，且F1恰是QF2的中点．若过A、Q、F2三点的圆恰好与直线l：x﹣y﹣3=0相切．
（1）求椭圆C的方程；
（2）设直线l1：y=x+2与椭圆C交于G、H两点．在x轴上是否存在点P（m，0），使得以PG，PH为邻边的平行四边形是菱形．如果存在，求出m的取值范围，如果不存在，请说明理由．

【考点】椭圆的简单性质．
【分析】（1）设椭圆C的半焦距为c（c＞0），由已知得过A、Q、F2三点的圆的圆心为F1（﹣c，0），半径2c=a， =2c，由此能求出椭圆的方程．
（2）将直线l1：y=x+2代入，得7x2+16x+4=0，由此利用韦达定理能求出GH的中点M，再由菱形的对角线互相垂直平分能求出存在满足题意的点P，且能求出m的值．
【解答】解：（1）设椭圆C的半焦距为c（c＞0），
∵椭圆C： +=1（a＞b＞0）的左、右焦点分别为F1，F2，上顶点为A，
过点A与AF2垂直的直线交x轴负半轴于点Q，且F1恰是QF2的中点，
过A、Q、F2三点的圆恰好与直线l：x﹣y﹣3=0相切，
∴过A、Q、F2三点的圆的圆心为F1（﹣c，0），半径2c=a，
又∵该项圆与直线l相切，∴=2c，
解得c=1，∴a2=4，b2=3，
∴所求椭圆的方程为．
（2）将直线l1：y=x+2代入，得7x2+16x+4=0，
设G（x1，y1），H（x2，y2），则，，
∴，
∴GH的中点M（﹣），
∵菱形的对角线互相垂直平分，∴kPA•kPB=﹣1，
∴，解得m=﹣，
∴存在满足题意的点P，且m的值为﹣．

　
21．已知函数f（x）=x2﹣mlnx，g（x）=x2﹣2x，F（x）=f（x）﹣g（x）
（Ⅰ）当m＞0，求函数f（x）的单调区间；
（Ⅱ）当m=﹣1时，试问过点（2，5）可作多少条直线与曲线y=F（x）相切？说明理由．
【考点】利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．
【分析】（I）求出函数的定义域，求出函数的导数，利用函数的导数的符号判断函数的单调性，求出单调区间．
（II） 先表示出过点（2，5）与曲线y=g（x）相切的直线，进而假设函数，可求得切线的条数．
【解答】解：（I）函数f（x）=x2﹣mlnx的定义域是（0，+∞）．
∵f′（x）=x﹣==
令f′（x）=0得：x=或x=﹣（舍去）．
由f′（x）＞0得x＞，∴此时f（x）是增函数；
由f′（x）＜0得0＜x＜，∴f（x）是减函数．
∴函数f（x）的增区间是（=，+∞），减区间是（0，）．
（II）设切点为（x1，y1）
当n=﹣1时，F（x）=f（x）﹣g（x）=lnx+2x，
F′（x）=+2，
切线方程为y﹣5=（+2）（x﹣2），切点在y=F（x）上，即y1=lnx1+2x1，
∴lnx1+2x1﹣5=（+2）（（x1﹣2），
即lnx1+﹣2=0，
令
∴，
由h′（x）=0可得，x=2，
由h′（x）＞0得x＞2，由h′（x）＜0，得x＜2，
∴h（x）在（0，2）上单调递减，在（2，+∞）上单调递增，
∴当x=2时，函数h（x）取得极小值同时也是最小值，
∵h（2）=ln2﹣1＜0，且h（）=2e﹣3＞0，h（e2）=＞0，
∴h（x）与x轴有两个交点∴过点（2，5）可作2条曲线y=g（x）的切线．
　
请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-1：几何证明选讲]
22．已知BC为圆O的直径，点A为圆周上一点，AD⊥BC于点D，过点A作圆O的切线交BC的延长线于点P，过点B作BE垂直PA的延长线于点E．求证：
（1）PA•PD=PE•PC；
（2）AD=AE．

【考点】与圆有关的比例线段．
【分析】（1）证明△APD∽△BPE，可得AP•PE=PD•PB，因为PA，PB分别为圆O的切线与割线，所以PA2=PB•PC，两式相除，即可证明PA•PD=PE•PC；
（2）连接AC，DE，证明A，D，B，E四点共圆且AB为直径，即可得出AD=AE．
【解答】证明：（1）因为AD⊥BP，BE⊥AP，
所以△APD∽△BPE，
所以，
所以AP•PE=PD•PB，
因为PA，PB分别为圆O的切线与割线，
所以PA2=PB•PC，
所以=，
所以PA•PD=PE•PC；
（2）连接AC，DE，
因为BC为圆O的直径，
所以∠BAC=90°，
所以AB⊥AC．
因为=，
所以AC∥DE，
所以AB⊥DE，
因为AD⊥BP，BE⊥AP，
所以A，D，B，E四点共圆且AB为直径，
因为AB⊥DE，
所以AD=AE．

　
[选修4-4：坐标系与参数方程]
23．已知直线l的参数方程为（t为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=4cos（θ﹣）
（Ⅰ）求曲线C的直角坐标方程；
（Ⅱ）若点P（x，y）是直线l上位于圆内的动点（含端点），求x+y的最大值和最小值．
【考点】简单曲线的极坐标方程．
【分析】（I）圆C的极坐标方程为ρ=4cos（θ﹣），展开可得：ρ2=4，把ρ2=x2+y2，x=ρcosθ，y=ρsinθ代入可得直角坐标方程．
（II）圆C的标准方程为： =4．设z=x+y．把直线l的参数方程（t为参数）代入z=x+y，可得：z=2﹣t，由于直线l经过圆心，kd 点P对应的参数满足﹣2≤t≤2即可得出．
【解答】解：（I）圆C的极坐标方程为ρ=4cos（θ﹣），展开可得：ρ2=4，
可得直角坐标方程：x2+y2﹣2x﹣2y=0．
（II）圆C的标准方程为： =4，圆心C，半径r=2．设z=x+y．
把直线l的参数方程（t为参数）代入z=x+y，可得：z=2﹣t，
由于直线l经过圆心，
∴点P对应的参数满足﹣2≤t≤2．
∴﹣2≤﹣t≤2+2．
即x+y的最大值和最小值分别为+2；2﹣2．
　
[选修4-5：不等式选讲]．
24．已知函数f（x）=m﹣|x﹣2|（m＞0），且f（x+2）≥0的解集为[﹣3，3]
（Ⅰ）求m的值；
（Ⅱ）若a＞0，b＞0，c＞0且++=，求证：2a+3b+4c≥9．
【考点】绝对值三角不等式．
【分析】（Ⅰ）根据绝对值不等式的解法进行求解即可．
（Ⅱ）由条件得++=1，利用1的代换，结合基本不等式进行证明求解即可．
【解答】解：（Ⅰ）∵f（x+2）=m﹣|x|，
由且f（x+2）≥0得m﹣|x|≥0，即|x|≤m，
即﹣m≤x≤m，
∵f（x+2）≥0的解集为[﹣3，3]
∴m=3；
证明：（Ⅱ）∵m=3，
∴++==1，
则2a+3b+4c=（2a+3b+4c）（++）=3++++++≥3+2+2+2=9，
当且仅当=， =， =，即2a=3b=4c，即a=，b=1，c=时，取等号．
即2a+3b+4c≥9成立．