山东省济南市天桥区2022-2023学年八年级下学期期末考试数学试题

这是一份山东省济南市天桥区2022-2023学年八年级下学期期末考试数学试题，共15页。试卷主要包含了已知a＜b，下列不等式成立的是，直线l1等内容，欢迎下载使用。
八年级下学期数学期末考试试题
满分：150分 时间：120分钟
一．单选题。（每小题4分，共40分）
1.下列四个标志中，既是轴对称图形又是中心对称图形的是（ ）
A. B. C. D.
2.已知a＜b，下列不等式成立的是（ ）
A.﹣2a＜﹣2b B.2a－1＞2b－1 C.a3＜b3 D.a+2＞b+2
3.下列式子中，从左边到右边的变形是因式分解的是（ ）
A.x2－4=（x+2）（x－2） B.（a+b）（a－b）=a2－b2
C.x2－x－2=x（x－1）－2 D.x－1=x（1－1x）
4、在平面直角坐标系中，将点P（2，﹣3）向右平移2个单位长度，再向上平移4个单位长度，得到的点P’的坐标是（ ）
A.（0，1） B.（4，1） C.（4，﹣1） D.（0，﹣1）
5、如图，在平行四边形ABCD中，AB=10，AD=7，∠ABC的平分线BE交CD于点E，则DE的长是（ ）
A.5 B.7 C.3 D.2.5

（第5题图） （第8题图）
6.关于x的一元二次方程x2+2x+k=0有实数根，则k的取值范围是（ ）
A.k＞1 B.k＜1 C.k≥1 D.k≤1
7.在双减政策的推动下，某校学生课后作业时长有了明显的减少，去年上半年平均每天作业时长为a小时，经过去年下半年和今年上半年两次调整后，现在平均每周作业时长为b小时，设每半年平均每周作业时长的下降率为x，则可可方程为（ ）
A.a（1－x）=b B.a（1－x）2=b C.b（1+x）=a D.a（1+x）2=b
8.直线l1：y=k1x+b与直线l2：y=k2x在同一平面直角坐标系中的图象如图，则关于x的不等式k1x+b＞k2x的解集为（ ）
A.x＞﹣1 B.x＜﹣1 C.x＞0 D.﹣1＜x＜0
9.如图，在Rt△ABC中，∠ACB=90°，AC=BC，将△ABC绕点A逆时针旋转15°得到Rt△AB’C’，B’C’交AB于点E，若图中阴影部分面积为23，则B’E的长为（ ）
A.23－2 B.3－2 C.2 D.1

（第9题图） （第10题图）
10.如图，正方形ABCD中，AB=32，点E为对角线AC上的动点，以DE为边作正方形DEFG，点H是CD上一点，且DH=23CD，连接GH，则GH的最小值为（ ）
A.2 B.22 C.1 D.2
二、填空题。（每小题4分，共24分）
11.分解因式：a2－2ab= 。
12.一个正多边形的每一个内角都是135°，这个正多边形的边数为 。
13.若分式方程mx－3－13－x=2有增根，则m的值为 。
14.关于x的方程x2－4x+m=0有一个根是﹣1，则另一个根为 。
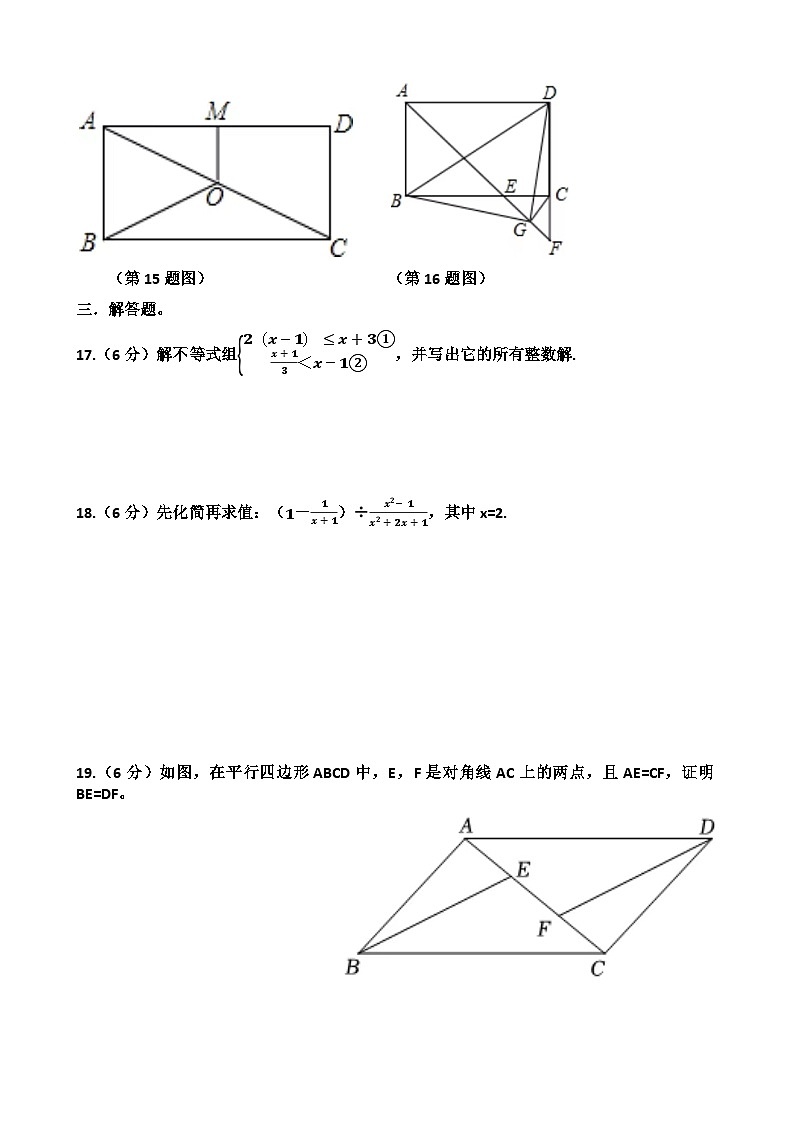
15.如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB=5，AD=12，则四边形ABOM的周长为 。
16.如图，在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，取EF的中点G，连接CG，BG，BD，DG，下列结论：①BE=CD；②∠DGF=135°；③∠ABG+∠ADG=180°；④若ABAD=23，则2S△BDG=13S△DGF，其中所有正确的结论是 。

（第15题图） （第16题图）
三．解答题。
17.（6分）解不等式组2（x－1）≤x+3①x+13＜x－1②，并写出它的所有整数解.





18.（6分）先化简再求值：（1－1x+1）÷x2－1x2+2x+1，其中x=2.











19.（6分）如图，在平行四边形ABCD中，E，F是对角线AC上的两点，且AE=CF，证明BE=DF。




20.（8分）（1）因式分解：2y2－8 （2）解方程x2+4x+3=0






21.（8分）在平面直角坐标系中，△ABC的位置如图所示，（每个小方格都是边长为1个单位长度的正方形）。
（1）若△ABC和△A1B1C1关于原点O成中心对称，画出△A1B1C1.
（2）将△ABC绕着点O顺时针旋转90°，画出旋转后得到的△AB2C2，并写出B2的坐标.
（3）在x轴上存在一点P，满足点P到点B1与点C1距离之和最小，请直接写出PB1+PC1的最小值为 。



22.（8分）如图，菱形ABCD的对角线AC与BD交于点O，分别过点C，点D作BD，AC的平行线交于点E，连接EO交CD于点F.
（1）证明：四边形DOCE是矩形；
（2）若AC=6，BD=8，求EF的长。




23.（10分）端午节吃粽子是中华民族的传统习俗，某超市节前购进了甲，乙两种畅销口味的粽子，已知购进甲种粽子的金额是1500元，购进乙种粽子的金额是1000元，购进甲种粽子的数量比乙种粽子的数量少50个，甲种粽子的单价是乙种粽子单价的2倍.
（1）求甲，乙两种粽子的单价分别是多少元.
（2）为满足消费者需求，该超市准备再次购进甲，乙两种粽子共200个，若总金额不超过1450元，问最多购进多少个甲种粽子.










24.（10分）阅读下列材料：
对于正数x，规定f（x）=xx+1，例如：f（2）=22+1=23.
（1）求值：f（3）+f（13）= ；f（4）+f（14）= .
（2）猜想f（x）+f（1x）= ，并证明你的猜想 ；
（3）应用：请结合（2）的结论，计算下面式子的值：
f（2023）+f（2022）+f（2021）+...+f（2）+f（1）+...+f（12）+...+f（12021）+f（12022）+f（12023）.



















25.（12分）已知一次函数的图象y=﹣34x+6与x轴，y轴分别交于点A，点B，与直线y=54x交于点C，过点B作x轴的平行线l，点P是直线l上的一个动点.
（1）求点A，点B的坐标.
（2）若S△AOC=S△BCP，求点P的坐标.
（3）若点E是直线y=54x上的一个动点，在平面内是否存在点F，使四边形APEF是正方形，若存在，请求出点E的坐标，若不存在，说明理由。




















26.（12分）在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点，（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF.
（1）观察猜想：如图1，当点D在线段BC上时，
①BC与CF的位置关系是 ;
②BC，CD，CF之间的数量关系是 .
（2）数学思考：如图2，当点D在线段BC的延长线上时，（1）中结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明.
（3）拓展延伸：如图3，在图2的情况下，延长BA交CF于点G，连接GE，若AB=22，CD=1，请求出GE的长.















答案解析
一．单选题。（每小题4分，共40分）
1.下列四个标志中，既是轴对称图形又是中心对称图形的是（ D ）
A. B. C. D.
2.已知a＜b，下列不等式成立的是（ C ）
A.﹣2a＜﹣2b B.2a－1＞2b－1 C.a3＜b3 D.a+2＞b+2
3.下列式子中，从左边到右边的变形是因式分解的是（ A ）
A.x2－4=（x+2）（x－2） B.（a+b）（a－b）=a2－b2
C.x2－x－2=x（x－1）－2 D.x－1=x（1－1x）
4、在平面直角坐标系中，将点P（2，﹣3）向右平移2个单位长度，再向上平移4个单位长度，得到的点P’的坐标是（ B ）
A.（0，1） B.（4，1） C.（4，﹣1） D.（0，﹣1）
5、如图，在平行四边形ABCD中，AB=10，AD=7，∠ABC的平分线BE交CD于点E，则DE的长是（ C ）
A.5 B.7 C.3 D.2.5

（第5题图） （第8题图）
6.关于x的一元二次方程x2+2x+k=0有实数根，则k的取值范围是（ D ）
A.k＞1 B.k＜1 C.k≥1 D.k≤1
7.在双减政策的推动下，某校学生课后作业时长有了明显的减少，去年上半年平均每天作业时长为a小时，经过去年下半年和今年上半年两次调整后，现在平均每周作业时长为b小时，设每半年平均每周作业时长的下降率为x，则可可方程为（ B ）
A.a（1－x）=b B.a（1－x）2=b C.b（1+x）=a D.a（1+x）2=b
8.直线l1：y=k1x+b与直线l2：y=k2x在同一平面直角坐标系中的图象如图，则关于x的不等式k1x+b＞k2x的解集为（ A ）
A.x＞﹣1 B.x＜﹣1 C.x＞0 D.﹣1＜x＜0
9.如图，在Rt△ABC中，∠ACB=90°，AC=BC，将△ABC绕点A逆时针旋转15°得到Rt△AB’C’，B’C’交AB于点E，若图中阴影部分面积为23，则B’E的长为（ A ）
A.23－2 B.3－2 C.2 D.1

（第9题图） （第10题图）
10.如图，正方形ABCD中，AB=32，点E为对角线AC上的动点，以DE为边作正方形DEFG，点H是CD上一点，且DH=23CD，连接GH，则GH的最小值为（ C ）
A.2 B.22 C.1 D.2
二、填空题。（每小题4分，共24分）
11.分解因式：a2－2ab= a（a－2b） 。
12.一个正多边形的每一个内角都是135°，这个正多边形的边数为 8 。
13.若分式方程mx－3－13－x=2有增根，则m的值为 ﹣1 。
14.关于x的方程x2－4x+m=0有一个根是﹣1，则另一个根为 x=5 。
15.如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB=5，AD=12，则四边形ABOM的周长为 20 。
16.如图，在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，取EF的中点G，连接CG，BG，BD，DG，下列结论：①BE=CD；②∠DGF=135°；③∠ABG+∠ADG=180°；④若ABAD=23，则2S△BDG=13S△DGF，其中所有正确的结论是 ①③④ 。

（第15题图） （第16题图）
三．解答题。
17.（6分）解不等式组2（x－1）≤x+3①x+13＜x－1②，并写出它的所有整数解.
解不等式①得x≤5
解不等式②得x＞2
不等式组解集为2＜x≤5
整数解为3，4，5

18.（6分）先化简再求值：（1－1x+1）÷x2－1x2+2x+1，其中x=2.
解：原式=xx+1×（x+1）2（x+1）（x－1）
=xx－1
将x=2代入得2



19.（6分）如图，在平行四边形ABCD中，E，F是对角线AC上的两点，且AE=CF，证明BE=DF。

证明：∵四边形ABCD是平行四边形
∴AB=CD AB∥CD
∴∠BAE=∠DCF
在△ABE和△CDF中
AE=CF∠BAE=∠DCFAB=CD
∴△ABE≌△CDF（SAS）
∴BE=DF

20.（8分）（1）因式分解：2y2－8 （2）解方程x2+4x+3=0

（1）=2（y2－4） （2）（x+1）（x+3）=0
=2（y+2）（y－2） x1=﹣1，x2=﹣3

21.（8分）在平面直角坐标系中，△ABC的位置如图所示，（每个小方格都是边长为1个单位长度的正方形）。
（1）若△ABC和△A1B1C1关于原点O成中心对称，画出△A1B1C1.
（2）将△ABC绕着点O顺时针旋转90°，画出旋转后得到的△AB2C2，并写出B2的坐标.
（3）在x轴上存在一点P，满足点P到点B1与点C1距离之和最小，请直接写出PB1+PC1的最小值为 。

（1）（2）
（3）26


22.（8分）如图，菱形ABCD的对角线AC与BD交于点O，分别过点C，点D作BD，AC的平行线交于点E，连接EO交CD于点F.
（1）证明：四边形DOCE是矩形；
（2）若AC=6，BD=8，求EF的长。

证：（1）∵CE∥BD，DE∥AC
∴四边形DECO是平行四边形
∵四边形ABCD是菱形
∴AC⊥BD
∴∠DOC=90°
∴四边形DOCE是矩形

（2）∵O是菱形ABCD对角线交点，且AC=6，BD=8
∴OC=3，OD=4 ∠DOC=90°
∴CD=32+42=5
∵F是矩形DOCE对角线交点
∴EF=12CD=52

23.（10分）端午节吃粽子是中华民族的传统习俗，某超市节前购进了甲，乙两种畅销口味的粽子，已知购进甲种粽子的金额是1500元，购进乙种粽子的金额是1000元，购进甲种粽子的数量比乙种粽子的数量少50个，甲种粽子的单价是乙种粽子单价的2倍.
（1）求甲，乙两种粽子的单价分别是多少元.
（2）为满足消费者需求，该超市准备再次购进甲，乙两种粽子共200个，若总金额不超过1450元，问最多购进多少个甲种粽子.

（1）解设：乙种粽子单价为x元，则甲种粽子单价为2x元
1000x－15002x=50
解得：x=5
经检验x=5是原方程的根
2x=2×5=10元
答：乙种粽子单价为5元，则甲种粽子单价为10元

（2）购进甲种粽子a个，则乙种粽子（200－a）个.
10a+5（200－a）≤1450
a≤90
答：甲种粽子最多购买90个.

24.（10分）阅读下列材料：
对于正数x，规定f（x）=xx+1，例如：f（2）=22+1=23.
（1）求值：f（3）+f（13）= ；f（4）+f（14）= .
（2）猜想f（x）+f（1x）= ，并证明你的猜想 ；
（3）应用：请结合（2）的结论，计算下面式子的值：
f（2023）+f（2022）+f（2021）+...+f（2）+f（1）+...+f（12）+...+f（12021）+f（12022）+f（12023）.

（1）1 1
（2）f（x）+f（1x）=1
证：f（x）+f（1x）=xx+1+1x1x+1=xx+1+1x+1=1


（3）=1+1+.....+1
=2023


25.（12分）已知一次函数的图象y=﹣34x+6与x轴，y轴分别交于点A，点B，与直线y=54x交于点C，过点B作x轴的平行线l，点P是直线l上的一个动点.
（1）求点A，点B的坐标.
（2）若S△AOC=S△BCP，求点P的坐标.
（3）若点E是直线y=54x上的一个动点，在平面内是否存在点F，使四边形APEF是正方形，若存在，请求出点E的坐标，若不存在，说明理由。


（1）令x=0代入y=﹣34x+6得
y=6
即B（0，6）
令y=0代入y=﹣34x+6得
x=8
即A（8，0）
（2）联立y=﹣34x+6y=54x
解得x=3y=154
C（3，154）
S△AOC=8×154÷2=15
∴S△AOC=S△BCP=15
以BP为底，高为6－154=94
∴BP=15×2÷94=403
即P（403，6）或（﹣403，6）
（3）（6，14）或（﹣6，﹣2）或（14，8）或（2，﹣8）














26.（12分）在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点，（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF.
（1）观察猜想：如图1，当点D在线段BC上时，
①BC与CF的位置关系是 ;
②BC，CD，CF之间的数量关系是 .
（2）数学思考：如图2，当点D在线段BC的延长线上时，（1）中结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明.
（3）拓展延伸：如图3，在图2的情况下，延长BA交CF于点G，连接GE，若AB=22，CD=1，请求出GE的长.

（1）①BC⊥CF ②BC=CD+CF
（2）BC⊥CF成立 BC=CD+CF不成立
∵正方形ADEF中，AD=AF，∠DAF=90°
∴∠BAC=∠DAF=90°
在△DAB和△FAC中
AD=AF∠BAD=∠CAFAB=AC
∴△DAB≌△FAC
∴∠ABD=∠ACF
∵∠BAC=90°，AB=AC
∴∠ACB=∠ABC=45°
∴∠ABD=135°
∴∠BCF=∠ACF－∠ACB=90°
∴BC⊥CF
∵CD=DB+BC， DB=CF
∴CD=CF+BC

（3）GE=10