江苏省南京师范大学附属中学2022-2023学年高一下学期5月月考数学试卷

这是一份江苏省南京师范大学附属中学2022-2023学年高一下学期5月月考数学试卷，共19页。
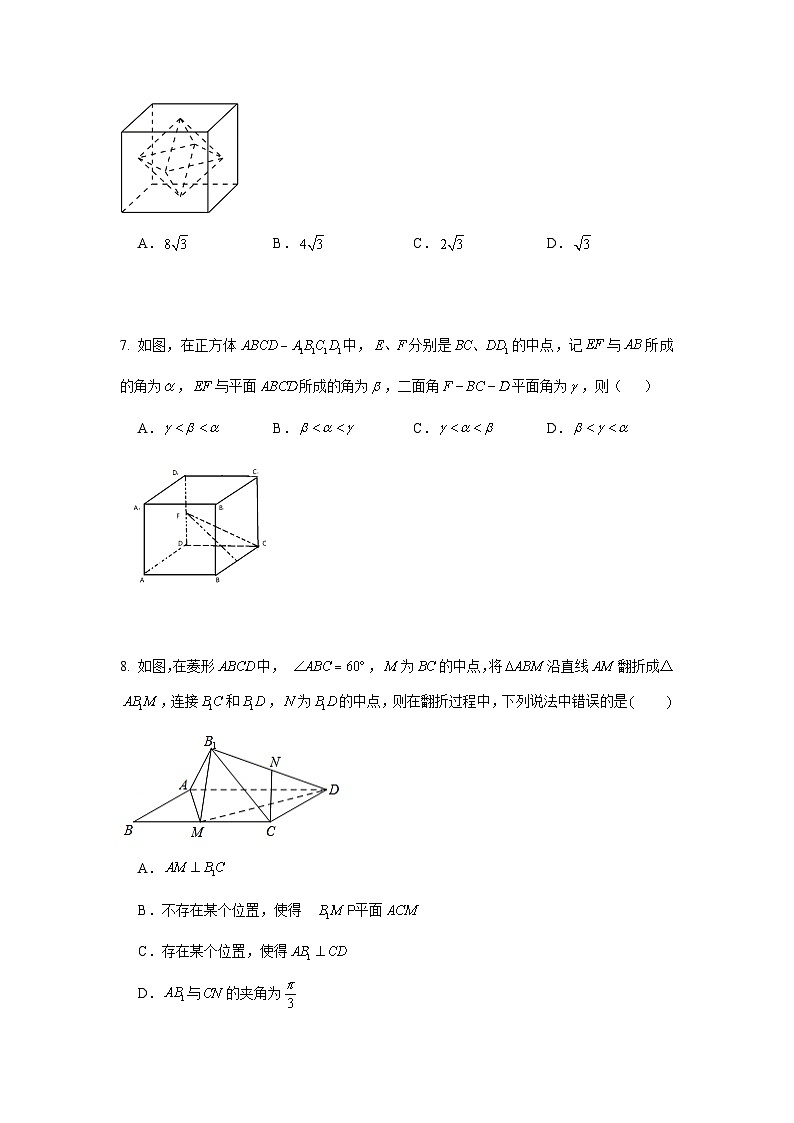
2022-2023学年南京师范大学附属中学高一5月月考一．单项选择题（本题共8小题，每小题4分，共32分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．若复数满足，其中为虚数单位，为的共轭复数，则=（    ）A． B．1 C．2 D．4 2. 若圆锥的母线长为1，其侧面展开图的面积为，则这个圆锥的体积为　　A． B． C． D．  3. 已知，则=（   ）A． B． C． D．  4. 北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步轨道卫星的轨道位于地球赤道所在平面，轨道高度为（轨道高度是指卫星到地球表面的距离）．将地球看作是一个球心为，半径为的球，若地球表面上的观测者与某颗地球静止同步轨道卫星处于相同经度，且能直接观测到，设点的维度（与赤道平面所成角的度数）的最大值为，则（    ）．A． B． C． D．  5. 点分别在空间四边形的边上，若，则下列说法中正确的是（   ）A．直线与一定平行 B．直线与一定相交C．直线与可能异面 D． 直线与一定共面 6. 如图，已知正方体的棱长为2，以其所有面的中心为顶点的多面体的表面积为　　A． B． C． D．  7. 如图，在正方体中，分别是的中点，记与所成的角为，与平面所成的角为，二面角平面角为，则（   ）A． B． C． D．
  8. 如图，在菱形中， ，为的中点，将沿直线翻折成△，连接和，为的中点，则在翻折过程中，下列说法中错误的是　　A． B．不存在某个位置，使得 平面C．存在某个位置，使得D．与的夹角为  二．多项选择题（本题共4小题，每小题4分，共16分，在每小题给出的选项中，有多项是符合题目要求的，全部选对的得4分，部分选对得得2分，有选错的得0分）9. 对于直线和平面，下列命题为真命题的有A．若 ，则B．若 ，则 C．若 ，则D．若 ，则  10.已知函数，若有且仅有一个实数，使得，则实数的值可能为（   ）A． B．1 C． D．3  11.在正方体中，点是线段上的动点，若过三点的平面将正方体截为两个部分，则所得截面的形状可能为（   ）A．等边三角形 B．矩形 C．菱形 D．等腰梯形 12.所有顶点都在两个平行平面内的多面体叫作拟柱体，拟柱体的侧面是三角形、梯形或平行四边形，如图，在拟柱体中，平面平面，分别是的中点，为四边形内一点，设四边形的面积的面积为，四边形的面积为，平面与平面的距离为，下列说法中正确的有（   ）A．直线与是异面直线 B．四边形的面积是的面积的4倍 C．挖去四棱锥与三棱锥后，拟柱体剩余部分的体积为 D．拟柱体的体积为 三．填空题：本题共4小题，每小题4分，共16分13. 已知向量，，且向量与共线，则实数　　．  14. 已知垂直于所在的平面，3，4，2，则点到平面的距离为_____________ 15.四面体每组对棱的棱长均相等，分别为，2，，则该四面体的体积为_______. 16.已知二面角的大小为，是等边三角形，是以点为直角顶点的等腰直角三角形，=2，则四面体的外接球的体积为 　　．  四．解答题：本题共3小题，共36分，解答应写出文字说明、证明过程或演算步骤.17. （12分）如图，在直三棱柱中，，分别为，的中点，．求证：（1）平面；（2）．    18. （12分）为了美化环境，某公园欲将一块空地规划建成休闲草坪，休闲草坪的形状为如图所示的四边形．并修建两条小路（路的宽度忽略不计），其中千米，千米，是以为直角顶点的等腰直角三角形．设，，．（1）当时，求小路的长度（千米）；（2）当草坪的面积最大时，求此时小路的长度（千米）．
  19. （12分）如图，在四棱锥中，底面是平行四边形，交于点，是上一点且平面（1）证明：为的中点；（2）在线段上是否存在点，使得平面平面，若存在，请给出点的位置，并证明，若不存在，请说明理由.
2022-2023学年南京师范大学附属中学高一5月月考一．单项选择题（本题共8小题，每小题4分，共32分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．若复数满足，其中为虚数单位，为的共轭复数，则=（    ）A． B．1 C．2 D．4【答案】【解析】2. 若圆锥的母线长为1，其侧面展开图的面积为，则这个圆锥的体积为　　A． B． C． D． 【答案】【解答】解：圆锥的侧面展开图扇形的弧长，设底面圆的半径为，则有，所以，于是圆锥的高为，该圆锥的体积为：．故选：．3. 已知，则=（   ）A． B． C． D． 【答案】【解答】4. 北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步轨道卫星的轨道位于地球赤道所在平面，轨道高度为（轨道高度是指卫星到地球表面的距离）．将地球看作是一个球心为，半径为的球，若地球表面上的观测者与某颗地球静止同步轨道卫星处于相同经度，且能直接观测到，设点的维度（与赤道平面所成角的度数）的最大值为，则（    ）．A． B． C． D． 【答案】【解答】解：设表示卫星，过作截面，截地球得大圆，过作圆的切线，，线段交圆于，如图，则，，，，则5. 点分别在空间四边形的边上，若，则下列说法中正确的是（   ）A．直线与一定平行 B．直线与一定相交C．直线与可能异面 D． 直线与一定共面【答案】【解析】因为，所以直线与一定共面6. 如图，已知正方体的棱长为2，以其所有面的中心为顶点的多面体的表面积为　　A． B． C． D．【答案】【解答】解：根据图形，已知正方体的棱长为2，易知正八面体的棱长为正方体面对角线长的一半，即为，如图，在正八面体中连接，，，可得，，互相垂直平分，为正八面体的中心，平面，平面，则，，．在中，，则该正八面体的体积，该八面体的表面积7. 如图，在正方体中，分别是的中点，记与所成的角为，与平面所成的角为，二面角平面角为，则（   ）A． B． C． D．
 【答案】【解析】设正方形边长为1，取中点，连接，连接连接8. 如图，在菱形中， ，为的中点，将沿直线翻折成△，连接和，为的中点，则在翻折过程中，下列说法中错误的是　　A． B．不存在某个位置，使得 平面C．存在某个位置，使得D．与的夹角为【答案】【解答】解：设，对于：因为四边形为菱形，，所以，则是等等边三角形，又因为为中心，所以，即，因为，又因为，平面，平面，所以平面，因为平面，所以，故正确；对于：连接交为，连接， 因为为的中点，所以不存在某个位置，使得平面，故正确；对于：因为（或补角）就是与所成的角，又，，所以，因为，所以，与所成角为，故正确； 二．多项选择题（本题共4小题，每小题4分，共16分，在每小题给出的选项中，有多项是符合题目要求的，全部选对的得4分，部分选对得得2分，有选错的得0分）9. 对于直线和平面，下列命题为真命题的有A．若 ，则B．若 ，则 C．若 ，则D．若 ，则【答案】【解析】对于A. 若 ，则不一定垂直，错误对于B. 若 ，则，又，所以平面内存在与平行的直线，设为直线，故可推出，因为，所以，正确对于C．若 ，则或，错误对于D．若，则直线分别与平面的法向量平行，故，正确 10.已知函数，若有且仅有一个实数，使得，则实数的值可能为（   ）A． B．1 C． D．3【答案】【解析】，因为在上有且仅有一个实数满足，则，解得，所以或 11.在正方体中，点是线段上的动点，若过三点的平面将正方体截为两个部分，则所得截面的形状可能为（   ）A．等边三角形 B．矩形 C．菱形 D．等腰梯形【答案】【解析】当点与重合时，过三点的平面是等边三角形，当点与重合时，过三点的平面是矩形，当点与中点重合时，过三点的平面是等腰梯形12.所有顶点都在两个平行平面内的多面体叫作拟柱体，拟柱体的侧面是三角形、梯形或平行四边形，如图，在拟柱体中，平面平面，分别是的中点，为四边形内一点，设四边形的面积的面积为，四边形的面积为，平面与平面的距离为，下列说法中正确的有（   ）A．直线与是异面直线 B．四边形的面积是的面积的4倍 C．挖去四棱锥与三棱锥后，拟柱体剩余部分的体积为 D．拟柱体的体积为【答案】【解析】对于A. 平面平面，，，共面，不共面，故直线与是异面直线，正确对于B.设，到的距离为，到距离为由上问可知，,所以四边形是梯形，因为分别是的中点，所以,所以，正确对于C．,故挖去四棱锥与三棱锥后，拟柱体剩余部分的体积为，正确故D错误三．填空题：本题共4小题，每小题4分，共16分13. 已知向量，，且向量与共线，则实数　　．【答案】【解答】解：向量，，向量与，向量与共线可得：，解得．故答案为：． 14. 已知垂直于所在的平面，3，4，2，则点到平面的距离为_____________【答案】【解答】解：垂直于所在的平面，，，，可得．底面三角形的面积为：棱锥是体积为：点到平面的距离为．，可得： ，15.四面体每组对棱的棱长均相等，分别为，2，，则该四面体的体积为_______.【答案】【解析】.四面体每组对棱的棱长均相等，分别为，2，，所以可将其补充为一个三个面上对角线长度分贝为，2，的长方体，所以长方体三边长分别为，，1，所以四面体体积为16.已知二面角的大小为，是等边三角形，是以点为直角顶点的等腰直角三角形，=2，则四面体的外接球的体积为 　　．【答案】【解答】解：如图，取的中点，连接，，由题意，2，，所以，，所以为二面角的平面角，所以，因为，是等边三角形，且，所以，又是以点为直角顶点的等腰直角三角形，所以1，过点作与平面垂直的直线，则球心在该直线上，设球的半径为，连接，，可得，在中，，利用余弦定理可得，所以，解得，所以其外接球的体积为．故答案为：． 四．解答题：本题共3小题，共36分，解答应写出文字说明、证明过程或演算步骤.17. （12分）如图，在直三棱柱中，，分别为，的中点，．求证：（1）平面；（2）．【答案】（1）见解析；（2）见解析【解答】证明：（1）在直三棱柱中，，分别为，的中点，，，，平面，平面，平面．解：（2）在直三棱柱中，是的中点，．，直三棱柱中，平面，平面，，又，平面，平面，．  18. （12分）为了美化环境，某公园欲将一块空地规划建成休闲草坪，休闲草坪的形状为如图所示的四边形．并修建两条小路（路的宽度忽略不计），其中千米，千米，是以为直角顶点的等腰直角三角形．设，，．（1）当时，求小路的长度（千米）；（2）当草坪的面积最大时，求此时小路的长度（千米）．
【答案】（1）5；（2）1【解答】解：（1）在中，由，又，．，由，解得：，是以为直角顶点的等腰直角三角形，，且，，在中，25，解得：5．（2）由（1）得：，此时，，且，当时，四边形的面积最大，即，此时，，所以，即1． 19. （12分）如图，在四棱锥中，底面是平行四边形，交于点，是上一点且平面（1）证明：为的中点；（2）在线段上是否存在点，使得平面平面，若存在，请给出点的位置，并证明，若不存在，请说明理由.【答案】（1）见解析；（2）存在，为中点时，平面平面【解析】（1）连接，设，连接，因为平面，平面，平面平面，所以，又底面为平行四边形，所以为的中点，所以为的中点．（2）存在，为中点时，平面平面因为为中点，为的中点，所以，由（1）可知,因为所以，平面平面