福建省泉州市安溪县2021-2022学年八年级下学期期末考试数学试卷(含解析)

这是一份福建省泉州市安溪县2021-2022学年八年级下学期期末考试数学试卷(含解析)，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
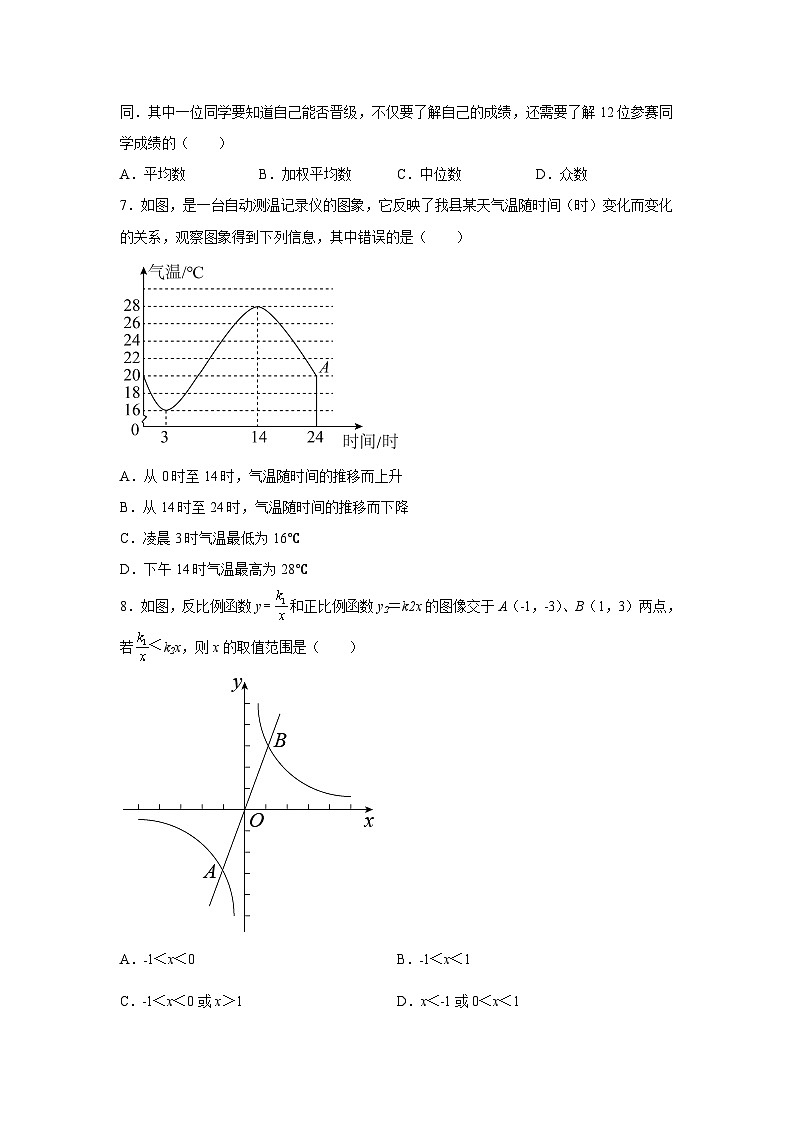
福建省泉州市安溪县2021-2022学年八年级下学期期末数学试题一、选择题1．下列式子中，是分式的是（　　）A． B．5x C．x D．2y2．如图，在平面直角坐标系中，被手盖住的点的坐标可能为（　　）A．(3，4) B．(﹣3，4) C．(﹣3，﹣4) D．(3，﹣4)3．下列等式中，从左到右变形不正确的是（　　）A． B．C．1 D．4．如图，在▱ABCD中，下列结论不正确的是（　　）A．AB＝CD B．▱ABCD是轴对称图形C．∠BAD＝∠BCD D．▱ABCD是中心对称图形5．下列性质中，菱形具有而矩形不一定具有的是（　　）A．对边平行且相等 B．对角线互相平分C．对角线相等 D．对角线互相垂直6．在一次选拔比赛中，有12位同学参加了“12进6”的淘汰赛，他们的比赛成绩各不相同．其中一位同学要知道自己能否晋级，不仅要了解自己的成绩，还需要了解12位参赛同学成绩的（　　）A．平均数 B．加权平均数 C．中位数 D．众数7．如图，是一台自动测温记录仪的图象，它反映了我县某天气温随时间（时）变化而变化的关系，观察图象得到下列信息，其中错误的是（　　）A．从0时至14时，气温随时间的推移而上升B．从14时至24时，气温随时间的推移而下降C．凌晨3时气温最低为16℃D．下午14时气温最高为28℃8．如图，反比例函数y和正比例函数y2＝k2x的图像交于A（﹣1，﹣3）、B（1，3）两点，若k2x，则x的取值范围是（　　）A．﹣1＜x＜0 B．﹣1＜x＜1C．﹣1＜x＜0或x＞1 D．x＜﹣1或0＜x＜19．四边形ABCD的对角线AC、BD相交于点O，且AD//BC，AD＝BC．下列条件：①AB＝CD；②AB＝AD；③AC＝BD；④AC⊥BD．要使四边形ABCD为正方形，须添加的条件是（　　）A．①② B．①③ C．①④ D．②③或③④10．如图四个都是反比例函数y的图像．其中阴影部分面积为6的个数是（　　）A．1个 B．2个 C．3个 D．4个二、填空题11．某病毒近似于球体，它的平均直径是0.00000008m，0.00000008用科学记数法表示为 _____．12．我县教育局拟招聘一批“2022届省内本科高校优秀师范毕业生”的数学教师，现有一名应聘者笔试成绩80分、面试成绩90分，综合成绩按照笔试占40%、面试占60%进行计算，该应聘者的综合成绩为 _____分．13．如图，把直线y＝﹣2x向上平移后得到直线AB，直线AB经过点A（0，1），则直线AB的解析式是 _____．14．关于x的分式方程1无解，则m＝_____．15．如图，在中，，，，为边上一动点，于，于，连接，则的最小值为______．16．如图，点A、B是反比例函数y图象上的两个动点，过点A、B分别作AC⊥x轴、BD⊥x轴，分别交反比例函数y图象于点C、D，得四边形ACBD是平行四边形．当点A、B不断运动时，现有以，结论：①▱ACBD可能是菱形；②▱ACBD不可能是矩形；③▱ACBD可能是正方形；④▱ACBD不可能是正方形．其中正确的是 _____．(写出所有正确结论的序号)三、解答题17．计算：(﹣1)2022+(）﹣1﹣(π﹣3.14)0．18．先化简，再求值：（1），其中x＝2022．19．如图，在矩形ABCD中，对角线AC、BD相交于点O，若∠BOC＝120°，AC＝2，求BC的长．20．在疫情防控形势下，人们在外出时都应戴上口罩以保护自己免受新型冠状病毒感染．某商店用4000元购进若干包一次性口罩，售完后又用7500元钱购进第二批这种口罩，所进的包数是第一批所进包数的1.5倍，每包口罩的进价比第一批每包口罩的进价多0.5元，求购进的第一批口罩有多少包？21．2022年春季，安溪县初中数学学科教学组编写“县本小单元分层作业”测试卷，现将某试点校八年级甲、乙两位选做“强基”层次的同学的10次测试成绩，绘制如图统计图．(1)根据图中提供的数据列出如表统计表：  平均成绩（分）众数（分）甲80b乙a90 则a＝　   　，b＝　   　．(2)现在要从这两位同学中选派一位参加数学素养竞赛，根据以上信息你认为应该选派谁？请简要说明理由．22．作图并证明(1)如图，在▱ACBD中，请按下列要求尺规作图：连结AC，作AC的垂直平分线分别交AC、BC、AD于点O、E、F，连接AE、CF．（不必写作法，保留作图痕迹）(2)求证：四边形AECF是菱形．23．受疫情影响，小林为了生计摆地摊，到批发市场进一批单价5元的小商品，在夜市营销中统计该批商品的销售单价x（元）与日销售量y（个）之间有如下关系：(1)猜测并确定y与x之间的函数关系式；(2)设经营此小商品的销售利润为w元，求出w与x之间的函数关系式．若物价局规定此小商品的售价最高不能超过9元/个，请你求出当日销售单价x定为多少时，才能获得最大日销售利润？销售单价x（元）67.27.58日销售量y（个）6050484524．【猜想结论】如图1，在△ABC中，点D、E分别是边AB、AC的中点，可以根据度量或目测猜想结论：DEBC，且DEBC．(1)【验证结论】如图2，在△ABC中，点D、E分别是边AB、AC的中点，延长DE至F，使得EF＝DE，连接FC．求证：DEBC，DEBC．(2)【应用结论】如图3，在四边形ABCD中，点E、F、G、H分别为边AB、BC、CD、DA的中点，顺次连接四边形ABCD各边中点得到新四边形EFGH，称为四边形ABCD中点四边形．应用上述验证结论，求解下列问题：①证明：四边形EFGH是平行四边形；②当AC、BD满足 　   　时，四边形EFGH是矩形；③当AC、BD满足 　   　时，四边形EFGH是正方形．25．如图，在平面直角坐标系中，一次函数y＝2x﹣1的图象分别交x轴、y轴于点A、B，将直线AB绕点B按顺时针方向旋转45°，交x轴于点C．(1)点A坐标是（ 　　，　　）、点B坐标是（ 　　，　　）；(2)求直线BC的函数表达式；(3)点M是射线BA上的点，在平面内是否存在点N，使得以M、N、B、C为顶点的四边形是菱形，如果存在，请求出点N的坐标；如果不存在，请说明理由．                           1．A解析：A、，分子分母均为整式且分母中含有字母，是分式，符合题意；B、，分母中不含字母，不是分式，不符合题意；C、，分母中不含字母，不是分式，不符合题意；D、，分母中不含字母，不是分式，不符合题意．故选A．2．C解析：解：∵手的位置是在第三象限，∴手盖住的点的横坐标小于0，纵坐标小于0，∴结合选项这个点是（-3，-4）．故选：C．3．D解析：解：A. ，正确，故该选项不符合题意；       B. ，正确，故该选项不符合题意；C. 1，正确，故该选项不符合题意；D. ，原变形不正确，故该选项符合题意．故选：D．4．B解析：解：A．平行四边形的对边相等，即AB＝CD，故选项A不合题意；B．▱ABCD不是轴对称图形，故选项B符合题意；C．平行四边形的对角相等，即∠BAD＝∠BCD，故选项C不合题意；D．▱ABCD是中心对称图形，故选项D不合题意；故选：B．5．D解析：解：A. 对边平行且相等，菱形和矩形都具有，故该选项不符合题意；       B. 对角线互相平分，菱形和矩形都具有，故该选项不符合题意；C. 对角线相等，矩形具有而菱形不具有，故该选项不符合题意；       D. 对角线互相垂直，菱形具有而矩形不一定具有，故该选项符合题意．故选：D．6．C解析：解：由于总共有12个人，且他们的分数互不相同，第6名和第7名同学的成绩的平均数是中位数，要判断是否能晋级，故应知道中位数的多少．故选：C．7．A解析：解：A．由图象可知，从0时至3时，气温随时间的推移而下降，故本选项符合题意；B．由图象可知，从14时至24时，气温随时间的推移而下降，说法正确，故本选项不合题意；C．由图象可知，凌晨3时气温最低为16℃，说法正确，故本选项不合题意；D．由图象可知，下午14时气温最高为28℃，说法正确，故本选项不合题意．故选：A．8．C解析：解：由图可知，在A点右侧，y轴左侧，反比例函数的值小于一次函数的值，此时﹣1＜x＜0；在B点右侧，反比例函数的值小于一次函数的值，此时x＞1；综上分析可知，当﹣1＜x＜0或x＞1时，k2x，故C正确．故选：C．9．D解析：解：∵AD∥BC，AD=BC∴四边形ABCD为平行四边形∵AC=BD∴平行四边形ABCD是矩形若AB=AD，则四边形ABCD为正方形；若AC⊥BD，则四边形ABCD是正方形．故选：D．10．B解析：解：第一个图形中阴影部分的面积为6，第二个图形中阴影部分面积为3，第三个图形中阴影部分面积为6，第四个图形中阴影部分面积为12．故选：B．11．解析：解：0.00000008＝8×10−8．故答案为：8×10−8．12．86解析：解：该应聘者的综合成绩为：80×40%＋90×60%＝86（分），故答案为：86．13．解析：解：由直线y=-2x向上平移后得到直线AB，故设直线AB的解析式是：y=-2x+b，∵直线AB经过点（0，1），∴b=1．∴直线AB的解析式是y=-2x+1．故答案是：y=-2x+1．14．4解析：解：原方程去分母得：x-m+x=x-2，解得：x=m-2，∵分式方程无解，∴x-2=0，即x=2，∴m-2=2，∴m=4．故答案为 415．解析：解：，，，，为直角三角形，，于，于，，四边形为矩形，连接，如图，，当的值最小时，的值最小，当时，的值最小，根据面积公式，，，的最小值为．故答案为：．16．①②④解析：解：设A(a,)，B(b,)，则C(a，-)，D(b,-)，∵AC=BD，∴-=，∴a=-b，∴yC=-=≠yB=，∴BC不与x轴平行，∴AC与BC不可能垂直，∴▱ACBD不可能是矩形，▱ACBD不可能是正方形．故③错误；②④正确；∵随着|a|不断变小，AC越来越大，BC越来越小，∴AC有可能与BC相等，故①正确；故答案为①②④．17．2解析：解：原式=1+2-1=2．18．，解析：解：（1）===，∴把x＝2022代入得：原式=．19．解析：解：∵∠BOC=120°，∴∠AOB=60°，∵四边形ABCD是矩形，∴AC=BD，AO=CO，BO=DO，∴AO=BO，∴△AOB是等边三角形，∴AO=BO=AB，∵AC=2，∴AO=AB=1，∵四边形ABCD是矩形，∴∠ABC=90°，由勾股定理得：BC=＝=．20．2000 包解析：解：设购进的第一批医用口罩有x包，则购进的第二批医用口罩有1.5x包，根据题意可得，解得，经检验，是原分式方程的解，且符合题意．答：购进的第一批医用口罩有2000包．21．(1)80、80(2)选乙(答案不唯一），理由见解析解析：（1）解：根据题意得：甲选做“强基”层次的同学的10次测试成绩为80，70，90，80，70，90，70，80，90，80，乙选做“强基”层次的同学的10次测试成绩为80，60，100，70，90，50， 90，70，90，100，∴甲选做“强基”层次的同学的10次测试成绩中，80出现的次数最多，∴a=80，乙选做“强基”层次的同学的10次测试成绩的平均数为，故答案为：80，80；（2）解：选乙，理由如下：甲和乙的平均分一样，而甲的众数是80，乙的众数是 90，即乙的众数比甲大．选甲也可以找出合适的理由，因此答案不唯一．22．(1)见解析(2)见解析解析：（1）解：如图：（2）证明：∵EF垂直平分线段AC，∴OA＝OC，EA＝EC，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠AFO＝∠CEO，在△AFO和△CEO中，，∴△AFO≌△CEO（AAS），∴AF＝EC，∵AF∥CE，∴四边形AECF是平行四边形，∵EA＝EC，∴平行四边形AECF是菱形．23．(1)(2)当日销售单价定为9元时，才能获得最大日销售利润值160元解析：（1）解：由表中数据可知，销售单价x与日销售量y的乘积为定值360，∴y与x之间的函数关系为反比例函数，设y与x之间的函数关系式为（k为常数且k≠0），把（6，60）代入解析式得 ，解得：k=360，∴y与x之间的函数关系式为；（2）解：由题意得：．∵，∴当x=9时，w最大，最大值为160，∴w与x之间的函数关系式为，当日销售单价x定为9元时，才能获得最大日销售利润．24．(1)见解析(2)①见解析；②垂直；③垂直且相等解析：（1）证明：∵点E为AC的中点，∴AE=CE，∵在△AED和△CEF中，∴，∴，，∴，∵点D为AB的中点，∴AD=BD，∴BD=CF，∴四边形BCFD为平行四边形，∴，，∵，∴，即DEBC，DEBC．（2）①连接AC、BD，如图所示：∵点E、F、G、H分别为边AB、BC、CD、DA的中点，∴，，，，∴，，∴四边形EFGH为平行四边形；②当AC⊥BD时， 四边形EFGH是矩形；根据解析①可知，，，四边形EFGH是平行四边形，∵AC⊥BD，∴，∵，∴，∵，∴，∴，∴四边形EFGH是矩形；故答案为：垂直；③当AC=BD且AC⊥BD时，四边形EFGH是正方形；根据解析②可知，当AC⊥BD时， 四边形EFGH是矩形，根据解析①可知，，，∵AC=BD，∴，∴四边形EFGH是正方形．故答案为：垂直且相等25．(1)，0； 0，1(2)(3)符合要求点 N 的坐标是（2， 2）、（ 1，2）、（3，2）．解析：（1）解：∵一次函数的图象分别交x、y轴于点A、B，∴令x=0，得y=-1，令y=0，则，∴，．故答案为：，0；0，-1；（2）解：过A作交BC于F，过F作轴于E．∵，∴是等腰直角三角形，∴．∵，∴，∴，∴，，∴，∴ ．设直线BC的函数表达式为，∴，∴，∴直线BC的函数表达式为：；（3）解：存在．如图，当BC是对角线时，四边形BMCN为菱形．∴，．∵直线BM为，∴设直线CN的函数表达式为．∵直线BC的函数表达式为：，∴，∴，解得，∴直线CN的函数表达式为，设．∵，，∴，∴，解得，∴点N的坐标为；如图，当BC是边，四边形BMNC为菱形时．∴，．∵直线BM为，∴设直线CN的函数表达式为．∵直线BC的函数表达式为：1，∴，∴，解得，∴直线CN的函数表达式为，设．∵，，∴，∴，解得或（不合题意，舍去），∴点N的坐标为；③如图，当BC是边，四边形BCMN为菱形时．∴，设．∵，，∴，∴，解得或0（不合题意，舍去），∴点M的坐标为．∵，，∴点N的坐标为．综上所述，满足条件的点N的坐标为（2， 2）、（ 1，2）、（3，2）．