江苏省泰州市姜堰区2021-2022学年七年级下学期期末学情调查数学试卷(含解析)

2022年春学期初中期末学情调查七年级数学试题

（考试时间：120分钟）

请注意：

1．所有试题的答案均填写在答题卡上，答案写在试卷上无效．

2．作图必须用2B铅笔，并请加黑加粗．

第一部分   选择题

一、选择题（本大题共有6小题，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）

1．下列计算正确的是（       ）

A． B． C． D．

2．下列各式从左到右的变形中，属于因式分解的是（       ）

A． B．

C． D．

3．若，则下列不等式成立的是（       ）

A． B． C． D．

4．下列命题中，真命题是（       ）

A．如果，，那么 B．平方后等于4的数是2

C．有公共顶点的两个角是对顶角 D．内错角相等

5．我国古代《算法统宗》里有这样一首诗：“我问开店李三公，众客都来到店中．一房七客多七客，一房九客一房空．”诗中后两句的意思是：如果每一间客房住满7人，那么有7人无房可住；如果每一间客房住满9人，那么就空出一间客房．设该店有客房x间、房客y人，则可列出关于x、y的二元一次方程组（       ）

A． B． C． D．

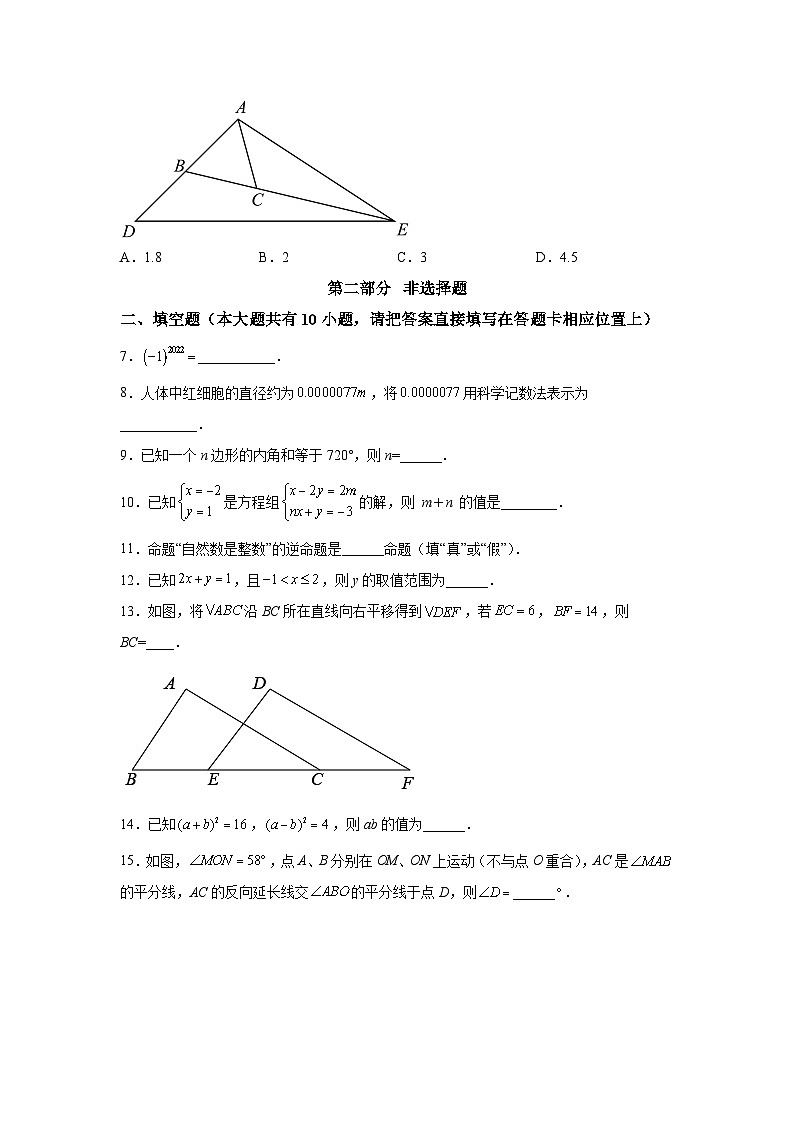
6．如图，在等边中，延长AB到点D，使得，延长BC到点E，使得，连接DE、AE，若，则为（       ）

A．1.8 B．2 C．3 D．4.5

第二部分   非选择题

二、填空题（本大题共有10小题，请把答案直接填写在答题卡相应位置上）

7．___________．

8．人体中红细胞的直径约为，将用科学记数法表示为___________．

9．已知一个n边形的内角和等于720°，则n=______．

10．已知是方程组的解，则 m＋n 的值是________．

11．命题“自然数是整数”的逆命题是______命题（填“真”或“假”）．

12．已知，且，则y的取值范围为______．

13．如图，将沿BC所在直线向右平移得到，若，，则BC=____．

14．已知，，则ab的值为______．

15．如图，，点A、B分别在OM、ON上运动（不与点O重合），AC是的平分线，AC的反向延长线交的平分线于点D，则______．

16．如图，在纸片中，，，且，P为BC上一点，将纸片沿AP剪开，并将、分别沿AB、AC向外翻折至、，连接DE，则面积的最小值为______．

三、解答题（本大题共10小题，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）

17．计算：

(1)

(2)

18．因式分解：

(1)；

(2)

19．解下列方程组或不等式组：

(1)；

(2)

20．先化简，再求值：，其中a为最大的负整数．

21．如图，在边长为1个单位长度的小正方形组成的网格中，点A、B、C都在格点上．

(1)利用网格画直线CD，使，且点D在格点上，并标出所有符合条件的格点D；

(2)在（1）的条件下，连接AD、BD，求的面积．

22．如图，点B、D分别在AE、CF上，EF分别交AD、BC于点M、N，，．

(1)AD与BC有怎样的位置关系？为什么？

(2)求证：．

23．政府为了更好的宣传“秸秆禁烧”，决定通过悬挂横幅与宣传牌进行专项宣传．已知制作5条横幅与制作2块宣传牌的费用一样，制作3条横幅与4块宣传牌共需1040元．

(1)求制作横幅与宣传牌的单价各是多少？

(2)政府计划共用2000元制作横幅和宣传牌（横幅和宣传牌都要有），且横幅的数量至少是宣传牌数量的2倍，则横幅和宣传牌可以有几种制作方案？

24．如图，直线EF分别交直线AB、CD于点M、N，，请从以下信息：①MG平分；②NH平分；③中选择两个作为补充条件，剩下的作为结论组成一个真命题，并加以证明．你选择      作为补充条件，      作为结论．（只填序号）

25．【情境呈现】在解方程组时，某同学发现：如果直接用代入消元法或加减消元法求解，运算量比较大，也容易出错，如果把方程组中的、分别看作一个整体，通过换元：令、，可以将原方程组化为，解得，把代入、，得，解得，所以原方程组解为．

(1)【灵活运用】若方程组的解为，则方程组的解为      ；

(2)【灵活运用】若方程组的解为，其中k为常数．

①求方程组的解：

②是否存在负整数k，使得①中方程组的解满足，若存在，请求出k的值；若不存在，请说明理由．

26．甲、乙两个长方形的边长如图所示（m为正整数），其周长分别为、．

(1)填空：=      ，=      （用含m的代数式表示、）；

(2)分别求出满足下列条件时m的值；

①与的和小于50；

②与的差为12；

(3)存在常数a，使得不论m为何值，的值始终为一个定值，试求出该定值及a的值．

1．A

解析：

解：A．，故A符合题意；

B．，故B不符合题意；

C．，故C不符合题意；

D．，故D不符合题意；

故选：A．

2．D

解析：

A.属于整式乘法，不是因式分解，故A不符合题意；

B.，原式分解错误，故B不符合题意；

C.没有变成几个因式乘积的形式，不是因式分解，故C不符合题意；

D.属于因式分解，故D符合题意．

3．B

解析：

A.根据不等式的两边乘（或除以）同一个正数，不等号的方向不变，若，则，故A错误；

B. 根据不等式的两边加（或减）同一个数，不等号的方向不变，若，则，故B正确；

C.根据不等式的两边乘（或除以）同一个负数，不等号的方向改变，若，则，故C错误；

D. 根据不等式的两边加（或减）同一个数，不等号的方向不变，若，则，故D错误；

故选 B

4．A

解析：

解：A.如果，，那么，此命题为真命题，故A符合题意；

B.平方后等于4的数是，原命题是假命题，故B不符合题意；

C.有公共顶点的两个角不一定是对顶角，原命题是假命题，故C不符合题意；

D.两直线平行，内错角相等，原命题是假命题，故D不符合题意．

故选：A．

5．B

解析：

根据题意得：，

故选：B．

6．C

解析：

解：∵，

∴，

∴，

∵，

∴，

即，

∴，故C正确．

故选：C．

7．1

解析：

解：1

故答案为：1．

8．

解析：

解：，

故答案为：．

9．6

解析：

解：由，

解得．

故答案为：6．

10．0

解析：

解：把代入方程组得：

，

解得：m=-2，n=2，

则m+n=2-2=0，

故答案为：0．

11．假

解析：

“自然数是整数”的逆命题是“整数是自然数”，是假命题，

故答案为：假．

12．##

解析：

解：，即，

由得，，

不等式，解得，

不等式，解得，

∴．

故答案为：．

13．10

解析：

解：由平移的性质可知，EF＝BC，

∴EF−EC＝BC−EC，即BE＝CF，

∵EC＝6，BF＝14，

∴BE＋CF＝14-6＝8，

∴BE＝CF＝4，

BC＝BE+EC＝4+6＝10

故答案为：10．

14．3

解析：

∵，

∴，

∴．

故答案为：3．

15．29

解析：

∵AC是的平分线，AC的反向延长线交的平分线于点D

∴

∵，

∴．

故答案为：29

16．

解析：

解：∵、分别沿AB、AC向外翻折至、

∴，

∴AP=AD=AE,∠BAD=∠BAP，∠CAP=∠CAE，

∵

所以∠DAE=∠DAP +∠PAE =2（∠BAP +∠PAC）=2∠BAC =90°，

面积=AD×AE=，当AP取最小值时的面积最小，

在中，当AP为BC边的高，即AP垂直BC时，AP最小，

此时，，

，解得：AP=，

面积的最小值为：．

17．(1)2

(2)

解析：(1)

解：

(2)

18．(1)

(2)

解析： (1)

原式＝；

(2)

原式＝．

19．(1)

(2)

解析： (1)

解：，

由①②，得：，

解得：，

将代入②，得：，

得，

所以原方程组的解是；

(2)

解：

解不等式①，得，

解不等式②，得，

不等式组的解集是．

20．；-7

解析：

解：

=

∵a为最大的负整数，

∴，

把代入得：原式．

21．(1)见解析

(2)3或7

解析： (1)

解：如图，将线段AB平移至CB1的位置，连接，

由图及勾股定理可得：，，，

∴，

∴∠B1CD1=90°，CD1⊥B1C，

∵B1C∥AB，

∴CD1⊥AB，

同理可得：CD2⊥AB．

(2)

如图，

，

，

∴的面积的面积为3或7．

22．(1)；理由见解析

(2)见解析

解析： (1)

解：；理由如下：

∵，，

又∵，

∴，

∴．

(2)

∵，

∴，

∴，

∵，

∴，

∴．

23．(1)制作横幅的单价为80元，制作宣传牌的单价为200元

(2)两种方案：①横幅20件，宣传牌2件；②横幅15件，宣传牌4件

解析：(1)

解：设制作横幅的单价为x元，制作宣传牌的单价为y元，根据题意得：

解得：

答：制作横幅的单价为80元，制作宣传牌的单价为200元．

(2)

设制作横幅m件，宣传牌n件，根据题意得：

，

∵m、n为正整数，

∴或，

答：有两种方案：①横幅20件，宣传牌2件；②横幅15件，宣传牌4件．

24．补充条件：①②，结论：③，见解析（答案不唯一）

解析：

补充条件：①②，结论：③，

证明如下：

∵MG平分，NH平分

∴，

∵

∴

∵

∴

∴

∴

∴

25．(1)

(2)①；②不存在，见解析

解析： (1)

解：∵的解为，

∴的解为，

令，，则方程组可变为：，

∴，解得：．

(2)

①令，，则可变为：，

∵的解为，

∴的解为，

即，解得：；

②不存在；

由①得：，

∵，

∴，

∴，

又∵k为负整数，

∴不存在．

26．(1)，

(2)①或；②

(3)始终为定值，

解析： (1)

，

(2)

①∵与的和小于50

∴

解得

∵m为正整数

∴或

②∵与的差为12

∴第一种情况：

，

解得

第二种情况：

，

解得（舍）

综上所述，与的差为12时

(3)

∴当时，即当时，不论m为何值，的值始终为定值