(新高考)高考数学一轮复习过关练考点12 y=Asin(wx+φ)的图像与性质（含解析）

考点12   y=Asin(wx+φ)的图像与性质

1、了解三角函数的周期性,画出 y =sin x , y =cos x , y =tan x 的图像,并能根据图像理解正弦函数、余弦函数在[ 0 ,2π ],正切函数的性质(如单调性、最大值和最小值、图像与 x 轴的交点等)

2. 了解三角函数 y = A sin ( ωx + φ )的实际意义及其参数 A , ω ,φ 对函数图像变化的影响;能画出 y = A sin (ωx +φ )的简图,能由正弦曲线 y =sin x 通过平移、伸缩变换得到 y = A sin ( ωx + φ )的图像 .

3. 会用三角函数解决一些简单的实际问题,体会三角函数是描述周期变化现象的重要函数模型 .

1. 三角函数的图像与性质是高考中的必考点,对这部分内容的考查,高考中大多以中、低档题为主,主要集中于对函数的周期、图像、单调性、值域(或最值)等几个方面的考查 . 要解决此类问题,要求学生熟练地掌握三角函数的图像,及正弦函数、余弦函数、正切函数的最基本的性质,并能运用这些性质去熟练地解题 .

2. 利用三角函数的性质解决问题时,要重视化归思想的运用,即将复杂的三角函数转化为基本的正弦、余弦、正切函数来处理

1、函数 f ( x ) = A sin ( ωx + φ )的图像的平移和伸缩变换以及根据图像确定 A , ω ,φ 问题是高考的热点,题型多样,难度中低档,主要考查识图、用图的能力,同时考查利用三角公式进行三角恒等变换的能力 .

2、要牢牢记住函数 f ( x ) = A sin ( ωx + φ )的图像和性质。

1、【2020年江苏卷】.将函数y=的图象向右平移个单位长度，则平移后的图象中与y轴最近的对称轴的方程是____.

【答案】

【解析】

当时

故答案为：

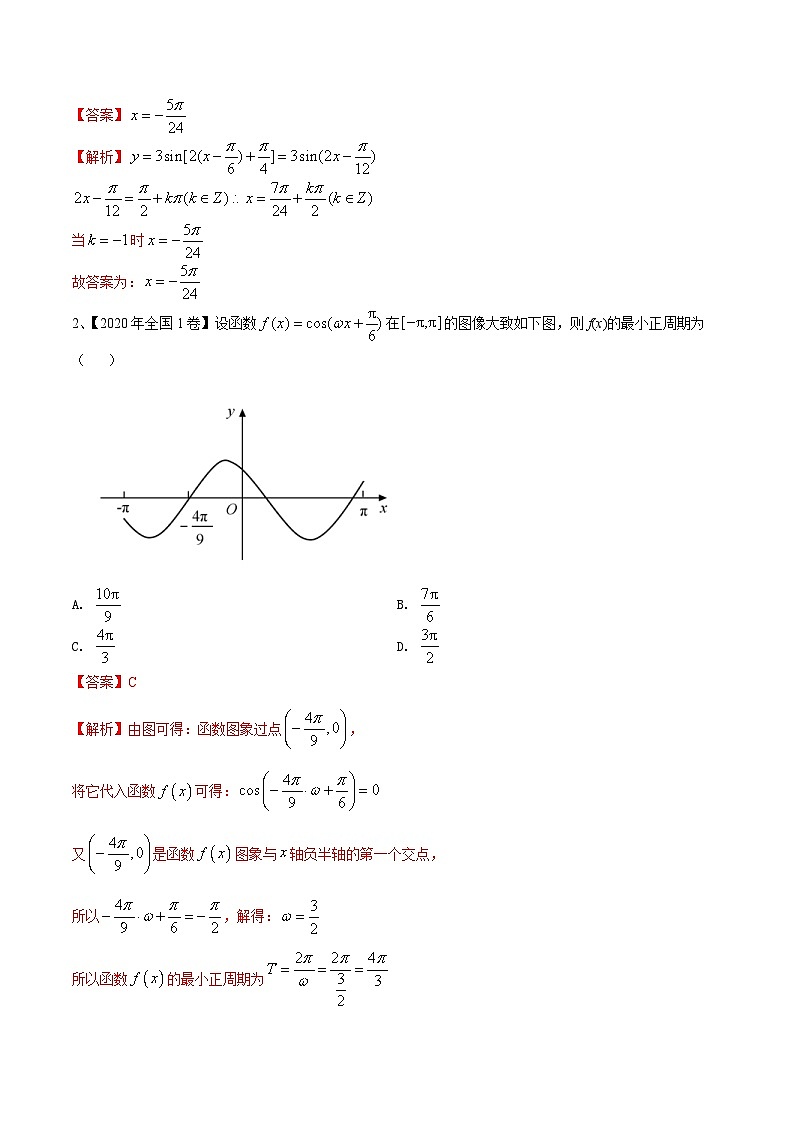
2、【2020年全国1卷】设函数在的图像大致如下图，则f(x)的最小正周期为（    ）

A.  B.

C.  D.

【答案】C

【解析】由图可得：函数图象过点，

将它代入函数可得：

又是函数图象与轴负半轴的第一个交点，

所以，解得：

所以函数的最小正周期为

故选：C

3、【2020年全国3卷】16.关于函数f（x）=有如下四个命题：

①f（x）的图像关于y轴对称．

②f（x）的图像关于原点对称．

③f（x）的图像关于直线x=对称．

④f（x）的最小值为2．

其中所有真命题的序号是__________．

【答案】②③

【解析】对于命题①，，，则，

所以，函数的图象不关于轴对称，命题①错误；

对于命题②，函数的定义域为，定义域关于原点对称，

，

所以，函数的图象关于原点对称，命题②正确；

对于命题③，，

，则，

所以，函数的图象关于直线对称，命题③正确；

对于命题④，当时，，则，

命题④错误.

故答案为：②③.

4、【2020年天津卷】8.已知函数．给出下列结论：

①的最小正周期为；

②是的最大值；

③把函数的图象上所有点向左平移个单位长度，可得到函数的图象．

其中所有正确结论的序号是

A. ① B. ①③ C. ②③ D. ①②③

【答案】B

【解析】因为，所以周期，故①正确；

，故②不正确；

将函数的图象上所有点向左平移个单位长度，得到的图象，

故③正确.

故选：B.

5、【2020年山东卷】.下图是函数y= sin(ωx+φ)的部分图像，则sin(ωx+φ)= （    ）

A.  B.  C.  D.

【答案】BC

【解析】由函数图像可知：，则，所以不选A,

当时，，

解得：，

即函数的解析式为：

.

而

故选：BC.

6、【2019年高考全国Ⅰ卷理数】函数f(x)=在的图像大致为

A． B．

C． D．

【答案】D

【解析】由，得是奇函数，其图象关于原点对称，排除A．又，排除B，C，故选D．

7、【2019年高考全国Ⅰ卷理数】关于函数有下述四个结论：

①f(x)是偶函数  ②f(x)在区间（，）单调递增

③f(x)在有4个零点 ④f(x)的最大值为2

其中所有正确结论的编号是

A．①②④   B．②④

C．①④  D．①③

【答案】C

【解析】为偶函数，故①正确．

当时，，它在区间单调递减，故②错误．

当时，，它有两个零点：；当时，

，它有一个零点：，故在有个零点：，故③错误．

当时，；当时，，又为偶函数，的最大值为，故④正确．

综上所述，①④正确，故选C．

8、【2019年高考全国Ⅱ卷理数】下列函数中，以为周期且在区间(，)单调递增的是

A．f(x)=|cos2x|     B．f(x)=|sin2x|    

C．f(x)=cos|x|      D．f(x)=sin|x|

【答案】A

【解析】作出因为的图象如下图1，知其不是周期函数，排除D；

因为，周期为，排除C；

作出图象如图2，由图象知，其周期为，在区间(，)单调递增，A正确；

作出的图象如图3，由图象知，其周期为，在区间(，)单调递减，排除B，

故选A．

图1

图2

图3

9、【2019年高考全国Ⅲ卷理数】设函数=sin（）(＞0)，已知在有且仅有5个零点，下述四个结论：

①在（）有且仅有3个极大值点

②在（）有且仅有2个极小值点

③在（）单调递增

④的取值范围是[)

其中所有正确结论的编号是

A．①④ B．②③

C．①②③ D．①③④

【答案】D

【解析】①若在上有5个零点，可画出大致图象，

由图1可知，在有且仅有3个极大值点.故①正确；

②由图1、2可知，在有且仅有2个或3个极小值点.故②错误；

④当=sin（）=0时，=kπ（k∈Z），所以，

因为在上有5个零点，

所以当k=5时，，当k=6时，，解得，

故④正确.

③函数=sin（）的增区间为：，.

取k=0，

当时，单调递增区间为，

当时，单调递增区间为，

综上可得，在单调递增.故③正确.

所以结论正确的有①③④.故本题正确答案为D.

10、【2019年高考天津卷理数】已知函数是奇函数，将的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图象对应的函数为．若的最小正周期为，且，则

A．  B．

C．  D．

【答案】C

【解析】∵为奇函数，∴；

又∴，

又，∴，

∴，故选C.

11、【2018年高考江苏卷】已知函数的图象关于直线对称，则的值是________．

【答案】

【解析】由题意可得，所以，

因为，所以

【名师点睛】由对称轴得，再根据限制范围求结果.函数（A>0，ω>0）的性质：

(1)；

(2)最小正周期；

(3)由求对称轴；

(4)由求增区间;由求减区间.

12、【2019年高考浙江卷】设函数.

（1）已知函数是偶函数，求的值；

（2）求函数的值域．

【答案】（1）或；（2）．

【解析】（1）因为是偶函数，所以，对任意实数x都有，

即，

故，

所以．

又，

因此或．

（2）

．

因此，函数的值域是．

题型一   三角函数的性质

1、（2020届山东省枣庄市高三上学期统考）设函数，若，(     )

A．2 B．-2 C．2019 D．-2019

【答案】B

【解析】

因为，

所以，

因此函数为奇函数，

又，所以.

故选B

2、（2020届山东省枣庄市高三上学期统考）已知函数的最小正周期为，且对，恒成立，若函数在上单调递减，则的最大值是（   ）

A． B． C． D．

【答案】B

【解析】

因为函数的最小正周期为，所以，

又对任意的，都使得，

所以函数在上取得最小值，则，，

即，

所以，

令，解得 ，

则函数在上单调递减，故的最大值是.

故选B

3、（2020届山东省潍坊市高三上期中）已知函数，则（    ）

A．的最小正周期为 B．图象的一条对称轴方程为

C．的最小值为 D．的上为增函数

【答案】B

【解析】

，

对A，的最小正周期为，故A错误；

对B，，图象的一条对称轴方程为，故B正确；

对C，的最小值为，故C错误；

对D，由，得，则在上先增后减，故D错误．

故选：B．

4、（2020届山东实验中学高三上期中）已知函数的图象关于直线对称，若，则的最小值为（    ）

A． B． C． D．

【答案】B

【解析】

的图象关于直线对称，

，

即，，

则，

，

，或，，

即，一个为最大值，一个为最小值，

则的最小值为，

，

的最小值为，

即的最小值为.

故选：．

5、（2020届山东省滨州市三校高三上学期联考）设函数，则下列结论正确的是（    ）

A．是的一个周期 B．的图像可由的图像向右平移得到

C．的一个零点为 D．的图像关于直线对称

【答案】ACD

【解析】

的最小正周期为，故也是其周期，故A正确；

的图像可由的图像向右平移得到，故B错误；

，故C正确；

，故D正确.

故选：ACD

6、.（2020届江苏省南通市如皋市高三下学期二模）已知函数，将函数的图象向右平移个单位长度后，所得图象与原函数图象重合，则的最小值等于__________.

【答案】4

【解析】由题得,

因为，所以的最小值等于4.

故答案为：4

7、（2020届江苏南通市高三基地学校第一次大联考数学试题）已知函数的图象关于点对称，则的最小值为_____.

【答案】.

【解析】由题意可得，

求得，
又，则的最小值为，
故答案为：.

8、(2019南京学情调研）已知函数f(x)＝2sin(2x＋φ)的图像关于直线x＝对称，则f(0)的值为________．

【答案】. 1

【解析】由题意，f＝2sin＝±2，即sin＝±1，又因为－＜φ＜， －<＋φ<，所以＋φ＝，即φ＝，所以f(x)＝2sin，f(0)＝1.

9、(2019苏锡常镇调研）函数的图像关于直线对称，则的最小值为       ．

【答案】

【解析】解法1：根据余弦函数的图像及性质，令，得，令得，，又因为，所以当时取得最小值为

解法2：由条件可得，即，则，，解得，，又因为，所以当时取得最小值为

解后反思：利用整体思想，结合三角函数的图像及性质是解决这类问题的关键！

10、(2019苏州期初调查） 已知函数f(x)＝sin(2x＋φ)(0≤φ<π)的一条对称轴是x＝－π，则φ＝________．

【答案】 　

【解析】因为函数f(x)的一条对称轴是x＝－π，所以2×＋φ＝kπ＋，k∈Z，则φ＝kπ＋，k∈Z，又因为0≤φ<π，所以φ＝.

11、(2019南京、盐城二模）若函数f(x)＝2sin(ωx＋φ)(ω>0，0<φ<π)的图像经过点，且相邻两条对称轴间的距离为，则f的值为________．

【答案】.　

【解析】由相邻两条对称轴间的距离为，知其最小正周期T＝2×＝π，从而得ω＝＝＝2，又f(x)＝2sin(2x＋φ)的图像经过点，所以2sin＝2，解得φ＝2kπ＋(k∈Z)，又因为0<φ<π，所以φ＝，故f(x)＝2sin，即有f＝2sin＝.

题型二 三角函数图像的变换

1、（2020届山东师范大学附中高三月考）为了得函数的图象，只需把函数的图象（   ）

A．向左平移个单位 B．向左平移单位

C．向右平移个单位 D．向右平移个单位

【答案】A

【解析】

不妨设函数的图象沿横轴所在直线平移个单位后得到函数的图象．

于是，函数平移个单位后得到函数，，即，

所以有，，取，．答案为A．

2、（2020届山东省枣庄、滕州市高三上期末）将曲线上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线，则（    ）

A．1 B．-1 C． D．

【答案】D

【解析】

把的图象向左平移个单位长度，得的图象，再把所得图象各点的横坐标变为原来的倍，纵坐标不变，得图象的函数式为，

，∴，

∴．

故选：D.

3、（2020届山东省潍坊市高三上学期统考）将函数的图像向右平移个单位得到函数的图像，则a的值可以为（  ）

A． B． C． D．

【答案】C

【解析】由题意知，，

其图像向左平移a个单位得到函数，

而函数，所以有

，取得.答案选C.

4、（2020届浙江省宁波市余姚中学高考模拟）函数f(x)＝sin(wx＋)(w＞0，＜)的最小正周期是π，若将该函数的图象向右平移个单位后得到的函数图象关于直线x＝对称，则函数f(x)的解析式为（   ）

A．f(x)＝sin(2x＋) B．f(x)＝sin(2x－)

C．f(x)＝sin(2x＋) D．f(x)＝sin(2x－)

【答案】D

【解析】因为函数的最小正周期是，

所以，解得，所以，

将该函数的图像向右平移个单位后，

得到图像所对应的函数解析式为，

由此函数图像关于直线对称，得：

，即，

取，得，满足，

所以函数的解析式为，故选D.

5、（2020·蒙阴县实验中学高三期末）关于函数的描述正确的是（    ）

A．其图象可由的图象向左平移个单位得到

B．在单调递增

C．在有2个零点

D．在的最小值为

【答案】ACD

【解析】由题：，

由的图象向左平移个单位，

得到，所以选项A正确；

令，得其增区间为

在单调递增，在单调递减，所以选项B不正确；

解，得：，，

所以取，所以选项C正确；

，，

所以选项D正确.

故选：ACD

6、（2020届山东省枣庄市高三上学期统考）将函数的图象向右平移个单位长度得到图象，则下列判断正确的是（    ）

A．函数在区间上单调递增

B．函数图象关于直线对称

C．函数在区间上单调递减

D．函数图象关于点对称

【答案】ABD

【解析】函数的图像向右平移个单位长度得到.

由于，故是的对称轴，B选项正确.

由于，故是的对称中心，D选项正确.

由，解得，即在区间上递增，故A选项正确、C选项错误.

故选：ABD.

7、(2019无锡期末） 已知直线y＝a(x＋2)(a>0) 与函数 y ＝|cosx|的图像恰有四个公共点A(x1，y1)，B(x2，y2)，C(x3，y3)，D(x4，y4), 其中 x1<x2<x3<x4，则x4＋＝________．

【答案】－2　

【解析】根据图形可得直线y＝a(x＋2)与函数y＝－cosx的图像相切于点(x4，－cosx4)，其中x4∈.因为y＝sinx，由导数的几何意义可得a＝sinx4＝，化简得x4＋＝－2.

8、（2020届江苏省南通市高三下学期3月开学考试）将函数（）的图象向左平移个单位长度后，所得图象关于直线对称，则的最小值为______.

【答案】

【解析】将函数f（x）＝sin（ωx）（ω＞0）的图象向左平移个单位后，可得函数y＝sin（ωx）的图象，再根据所得图象关于直线x＝π对称，可得ωπkπ，k∈Z，

∴当k＝0时，ω取得最小值为，

故答案为．

题型三  三角函数的解析式

1、（2020届山东省滨州市高三上期末）已知函数的图象过点，则(     )

A．把的图象向右平移个单位得到函数的图象

B．函数在区间上单调递减

C．函数在区间内有五个零点

D．函数在区间上的最小值为1

【答案】D

【解析】因为函数的图象过点，

所以，因此，

所以，

因此；

A选项，把的图象向右平移个单位得到函数的图象，故A错；

B选项，由得，即函数的单调递减区间是：，故B错；

C选项，由得，即，

因此，所以，共四个零点，故C错；

D选项，因为，所以，因此，所以，即的最小值为1，故D正确；

故选：D.

2、（2020·浙江温州中学3月高考模拟）已知（）过点，且当时，函数取得最大值1.

（1）将函数的图象向右平移个单位得到函数，求函数的表达式；

（2）在（1）的条件下，函数，求在上的值域.

【答案】(1)；(2).

【解析】 (1)由函数取得最大值1，可得,函数过得，

，∵，∴

，.

(2) ，

，

，值域为.