高考数学二轮专题学与练 11 空间几何体（考点解读）（含解析）

这是一份高考数学二轮专题学与练 11 空间几何体（考点解读）（含解析），共27页。

专题11 空间几何体

1．以选择、填空题形式考查空间位置关系的判断，及文字语言、图形语言、符号语言的转换，难度适中；
2．以熟悉的几何体为背景，考查多面体或旋转体的侧面积、表面积和体积计算，间接考查空间位置关系的判断及转化思想等，常以三视图形式给出几何体，辅以考查识图、用图能力及空间想象能力，难度中等．
3.几何体的三视图与表(侧)面积、体积计算结合；

1．柱体、锥体、台体、球的结构特征
名称
几何特征
棱柱
①有两个面互相平行(底面可以是任意多边形)；
②其余各面都是平行四边形，并且每相邻两个四边形的公共边互相平行
棱锥
①有一个面是多边形(底面)；
②其余各面是有公共顶点的三角形．
棱台
①底面互相平行；
②所有侧棱延长后交于一点(即原棱锥的顶点)
圆柱
①有两个互相平行的圆面(底面)；
②有一个侧面是曲面(母线绕轴旋转一周形成的)，且母线与底面垂直
圆台
①底面互相平行；
②有一个侧面是曲面，可以看成母线绕轴旋转一周形成的
球
①有一个曲面是球面；
②有一个球心和一条半径长R，球是一个几何体(包括内部)，可以看成半圆以它的直径所在直线为旋转轴旋转一周形成的
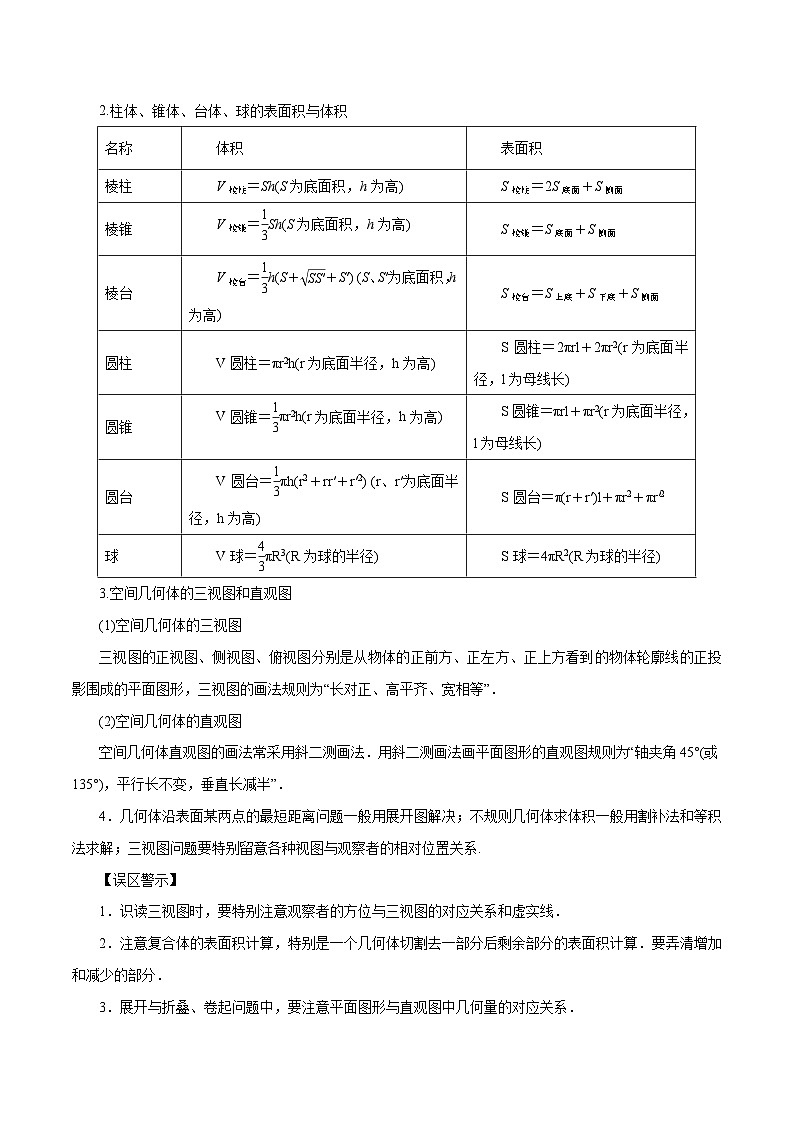
2.柱体、锥体、台体、球的表面积与体积
名称
体积
表面积
棱柱
V棱柱＝Sh(S为底面积，h为高)
S棱柱＝2S底面＋S侧面
棱锥
V棱锥＝Sh(S为底面积，h为高)
S棱锥＝S底面＋S侧面
棱台
V棱台＝h(S＋＋S′) (S、S′为底面积，h为高)
S棱台＝S上底＋S下底＋S侧面
圆柱
V圆柱＝πr2h(r为底面半径，h为高)
S圆柱＝2πrl＋2πr2(r为底面半径，l为母线长)
圆锥
V圆锥＝πr2h(r为底面半径，h为高)
S圆锥＝πrl＋πr2(r为底面半径，l为母线长)
圆台
V圆台＝πh(r2＋rr′＋r′2) (r、r′为底面半径，h为高)
S圆台＝π(r＋r′)l＋πr2＋πr′2
球
V球＝πR3(R为球的半径)
S球＝4πR2(R为球的半径)
3.空间几何体的三视图和直观图
(1)空间几何体的三视图
三视图的正视图、侧视图、俯视图分别是从物体的正前方、正左方、正上方看到的物体轮廓线的正投影围成的平面图形，三视图的画法规则为“长对正、高平齐、宽相等”．
(2)空间几何体的直观图
空间几何体直观图的画法常采用斜二测画法．用斜二测画法画平面图形的直观图规则为“轴夹角45°(或135°)，平行长不变，垂直长减半”．
4．几何体沿表面某两点的最短距离问题一般用展开图解决；不规则几何体求体积一般用割补法和等积法求解；三视图问题要特别留意各种视图与观察者的相对位置关系.
【误区警示】
1．识读三视图时，要特别注意观察者的方位与三视图的对应关系和虚实线．
2．注意复合体的表面积计算，特别是一个几何体切割去一部分后剩余部分的表面积计算．要弄清增加和减少的部分．
3．展开与折叠、卷起问题中，要注意平面图形与直观图中几何量的对应关系．

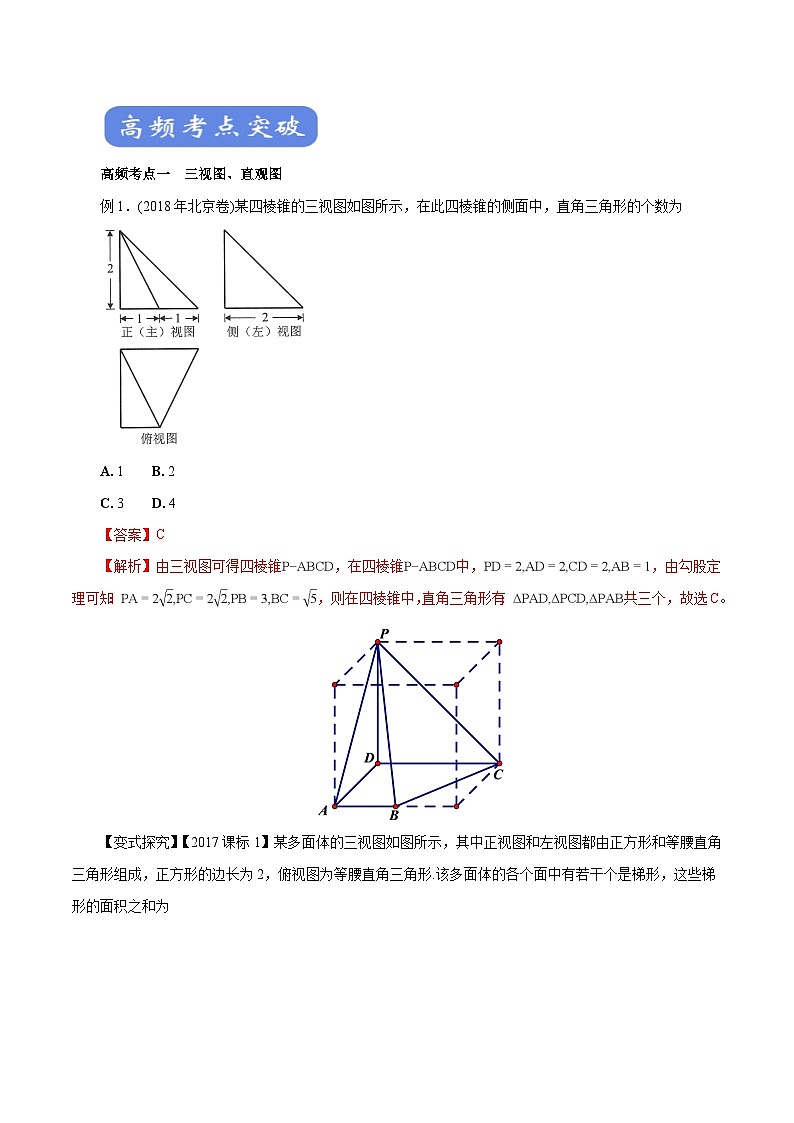
高频考点一　三视图、直观图
例1．(2018年北京卷)某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为

A. 1 B. 2
C. 3 D. 4
【答案】C
【解析】由三视图可得四棱锥，在四棱锥中，，由勾股定理可知：，则在四棱锥中，直角三角形有：共三个，故选C。

【变式探究】【2017课标1】某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为

A．10 B．12 C．14 D．16
【答案】B
【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成，如下图，则该几何体各面内只有两个相同的梯形，则这些梯形的面积之和为，故选B.

【变式探究】下图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( )

(A) (B) (C) (D)
【答案】C
【解析】由题意可知，圆柱的侧面积为，圆锥的侧面积为，圆柱的底面面积为，故该几何体的表面积为，故选C.
【变式探究】某三棱锥的三视图如图所示，则该三棱锥的表面积是(　　)

A．2＋ B．4＋ C．2＋2 D．5
【解析】该三棱锥的直观图如图所示：过D作DE⊥BC，交BC于E，连接AE，则BC＝2，EC＝1，AD＝1，ED＝2，

S表＝S△BCD＋S△ACD＋S△ABD＋S△ABC＝×2×2＋××1＋××1＋×2×＝2＋2.
【答案】C
高频考点二　几何体的表面积
例2．(2019·高考全国卷Ⅲ)学生到工厂劳动实践，利用3D打印技术制作模型．如图，该模型为长方体ABCD－A1B1C1D1挖去四棱锥O－EFGH后所得的几何体，其中O为长方体的中心，E，F，G，H分别为所在棱的中点，AB＝BC＝6 cm，AA1＝4 cm.3D打印所用原料密度为0.9 g/cm3.不考虑打印损耗，制作该模型所需原料的质量为________g.

【解析】由题易得长方体ABCD­A1B1C1D1的体积为6×6×4＝144(cm3)，四边形EFGH为平行四边形，如图所示，连接GE，HF，易知四边形EFGH的面积为矩形BCC1B1面积的一半，即×6×4＝12(cm2)，所以V四棱锥O­EFGH＝×3×12＝12(cm3)，所以该模型的体积为144－12＝132(cm3)，所以制作该模型所需原料的质量为132×0.9＝118.8(g)．

【答案】118.8
【举一反三】(2018·高考全国卷Ⅱ)已知圆锥的顶点为S，母线SA，SB所成角的余弦值为，SA与圆锥底面所成角为45°.若△SAB的面积为5，则该圆锥的侧面积为________．
【解析】如图所示，设S在底面的射影为S′，连接AS′，SS′.△SAB的面积为·SA·SB·sin∠ASB＝·SA2·＝·SA2＝5，所以SA2＝80，SA＝4.因为SA与底面所成的角为45°，所以∠SAS′＝45°，AS′＝SA·cos 45°＝4×＝2.所以底面周长l＝2π·AS′＝4π，所以圆锥的侧面积为×4×4π＝40π.

【答案】40π
【变式探究】(1)已知某几何体是一个平面将一正方体截去一部分后所得，该几何体的三视图如图所示，则该几何体的表面积为(　　)

A．20＋2　　　　　 B．18＋2
C．18＋ D．20＋
(2)已知某几何体的三视图如图，则该几何体的表面积是(　　)

A．＋3 B．＋3
C． D．
【解析】(1)如图所示，ABCD-A1B1C1D1是棱长为2的正方体，根据三视图，还原几何体的直观图为图中多面体ABCD­A1C1D1，其表面积为S正方形ABCD＋S＋S＋S＋S＋S＋S＝4＋4＋4＋2＋2＋2＋×8＝18＋2，故选B．

(2)由三视图知，该几何体为圆锥挖掉圆台后剩余部分，其表面积S表＝π×22＋π×12＋××4＋××2＋×2＝＋3.故选A．
【答案】(1)B　(2)A
【变式探究】一个几何体的三视图如图所示，则该几何体的表面积为(　　)

A．3π B．4π C．2π＋4 D．3π＋4
【解析】由三视图可知原几何体为半圆柱，底面半径为1，高为2，则表面积为：
S＝2×π×12＋×2π×1×2＋2×2
＝π＋2π＋4＝3π＋4.
【答案】D
高频考点三　几何体的体积
例3．(2018年江苏卷)如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为________．

【答案】
【解析】由图可知，该多面体为两个全等正四棱锥的组合体，正四棱锥的高为1，底面正方形的边长等于，所以该多面体的体积为
【变式探究】某几何体的三视图如图所示，则该几何体的体积为(　　)

A.＋π B.＋π C.＋2π D.＋2π
【解析】这是一个三棱锥与半个圆柱的组合体，V＝π×12×2＋××1＝π＋，选A.
【答案】A
【变式探究】已知一所有棱长都是的三棱锥，则该三棱锥的体积为________．
【解析】记所有棱长都是的三棱锥为P­ABC，如图所示，取BC的中点D，连接AD，PD，作PO⊥AD于点O，则PO⊥平面ABC，且OP＝×＝，故三棱锥P­ABC的体积V＝S△ABC·OP＝××()2×＝.

【答案】
高频考点四 与球有关的切、接问题
例4．(2019·高考全国卷Ⅰ )已知三棱锥P­ABC的四个顶点在球O的球面上，PA＝PB＝PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF＝90°，则球O的体积为(　　)
A．8π B．4π
C．2π D．π
【答案】D
【解析】因为点E，F分别为PA，AB的中点，所以EF∥PB，
因为∠CEF＝90°，所以EF⊥CE，所以PB⊥CE.
取AC的中点D，连接BD，PD，易证AC⊥平面BDP，
所以PB⊥AC，又AC∩CE＝C，AC，CE⊂平面PAC，所以PB⊥平面PAC，
所以PB⊥PA，PB⊥PC，因为PA＝PB＝PC，△ABC为正三角形，
所以PA⊥PC，即PA，PB，PC两两垂直，将三棱锥P-ABC 放在正方体中如图所示．因为AB＝2，所以该正方体的棱长为，所以该正方体的体对角线长为，所以三棱锥P­ABC的外接球的半径R＝，所以球O的体积V＝πR3＝π＝π，故选D．

【举一反三】(2018·高考全国卷Ⅲ)设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且其面积为9，则三棱锥D­ABC体积的最大值为(　　)
A．12 B．18
C．24 D．54
【答案】B
【解析】设等边三角形ABC的边长为x，则x2sin 60°＝9，得x＝6.设△ABC的外接圆半径为r，则2r＝，解得r＝2，所以球心到△ABC所在平面的距离d＝＝2，则点D到平面ABC的最大距离d1＝d＋4＝6，所以三棱锥D­ABC体积的最大值Vmax＝S△ABC×6＝×9×6＝18.
【变式探究】(2017·高考全国卷Ⅲ)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为(　　)
A．π B．
C． D．
【答案】B
【解析】设圆柱的底面半径为r，则r2＝12－＝，所以，圆柱的体积V＝π×1＝，故选B．
【变式探究】如图，在四棱锥P­ABCD中，底面ABCD为菱形，PB⊥底面ABCD，O为对角线AC与BD的交点，若PB＝1，∠APB＝∠BAD＝，则三棱锥P­AOB的外接球的体积是________．

【解析】因为四边形ABCD是菱形，所以AC⊥BD，即OA⊥OB，因为PB⊥平面ABCD，所以PB⊥AO，又OB∩PB＝B，所以AO⊥平面PBO，所以AO⊥PO，即△PAO是以PA为斜边的直角三角形，因为PB⊥AB，所以△PAB是以PA为斜边的直角三角形，所以三棱锥P­AOB的外接球的直径为PA，因为PB＝1，∠APB＝，所以PA＝2，所以三棱锥P­AOB的外接球的半径为1，所以三棱锥P­AOB的外接球的体积为.
【答案】　
【举一反三】在四棱锥P­ABCD中，四边形ABCD是边长为2a的正方形，PD⊥底面ABCD，且PD＝2a，若在这个四棱锥内放一个球，则该球半径的最大值为________．
【解析】方法一：由题意知，球内切于四棱锥P­ABCD时半径最大，设该四棱锥的内切球的球心为O，半径为r，连接OA，OB，OC，OD，OP，则VP-ABCD＝VO-ABCD＋VO-PAD＋VO-PAB＋VO-PBC＋VO-PCD，即×2a×2a×2a＝××r，解得r＝(2－)a.
方法二：易知当球内切于四棱锥P­ABCD，即与四棱锥P­ABCD各个面均相切时，球的半径最大，作出相切时的侧视图如图所示，设四棱锥P­ABCD内切球的半径为r，则×2a×2a＝×(2a＋2a＋2a)×r，解得r＝(2－)a.

【答案】(2－)a

1．【2019年高考全国Ⅰ卷理数】已知三棱锥P−ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF=90°，则球O的体积为
A． B．
C． D．
【答案】D
【解析】解法一：为边长为2的等边三角形，为正三棱锥，
，又，分别为，的中点，，，又，平面，∴平面，，为正方体的一部分，，即，故选D．

解法二：设，分别为的中点，，且，为边长为2的等边三角形，，
又，，
中，由余弦定理可得，
作于，，为的中点，，，
，，
又，两两垂直，，，，故选D.

2．【2019年高考浙江卷】祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V柱体=Sh，其中S是柱体的底面积，h是柱体的高．若某柱体的三视图如图所示(单位：cm)，则该柱体的体积(单位：cm3)是

A．158 B．162
C．182 D．324
【答案】B
【解析】由三视图得该棱柱的高为6，底面可以看作是由两个直角梯形组合而成的，其中一个上底为4，下底为6，高为3，另一个的上底为2，下底为6，高为3，则该棱柱的体积为.
故选B.
3．【2019年高考全国Ⅲ卷理数】学生到工厂劳动实践，利用3D打印技术制作模型.如图，该模型为长方体挖去四棱锥O—EFGH后所得的几何体，其中O为长方体的中心，E，F，G，H分别为所在棱的中点，，3D打印所用原料密度为0.9 g/cm3，不考虑打印损耗，制作该模型所需原料的质量为___________g.

【答案】118.8
【解析】由题意得，，
∵四棱锥O−EFGH的高为3cm， ∴．
又长方体的体积为，
所以该模型体积为，
其质量为．
4．【2019年高考北京卷理数】某几何体是由一个正方体去掉一个四棱柱所得，其三视图如图所示．如果网格纸上小正方形的边长为1，那么该几何体的体积为__________．

【答案】40
【解析】如图所示，在棱长为4的正方体中，三视图对应的几何体为正方体去掉棱柱之后余下的几何体，

则几何体的体积.
5．【2019年高考天津卷理数】已知四棱锥的底面是边长为的正方形，侧棱长均为．若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为_____________．
【答案】
【解析】由题意，四棱锥的底面是边长为的正方形，侧棱长均为，借助勾股定理，可知四棱锥的高为.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，一个底面的圆心为四棱锥底面的中心，故圆柱的高为，圆柱的底面半径为，故圆柱的体积为.
6．【2019年高考江苏卷】如图，长方体的体积是120，E为的中点，则三棱锥E−BCD的体积是 ▲ .

【答案】10
【解析】因为长方体的体积为120，所以，
因为为的中点，所以，
由长方体的性质知底面，
所以是三棱锥的底面上的高，
所以三棱锥的体积.
1. (2018年北京卷)某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为

A. 1 B. 2
C. 3 D. 4
【答案】C
【解析】由三视图可得四棱锥，在四棱锥中，，由勾股定理可知：，则在四棱锥中，直角三角形有：共三个，故选C。

2. (2018年全国Ⅲ卷)中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是


A. A B. B C. C D. D
【答案】A
【解析】观擦图形图可知，俯视图为，故答案为A.
3. (2018年浙江卷)某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm3)是

A. 2 B. 4 C. 6 D. 8
【答案】C
【解析】根据三视图可得几何体为一个直四棱柱，高为2，底面为直角梯形，上下底分别为1，2，梯形的高为2，因此几何体的体积为选C.
4. (2018年浙江卷)已知四棱锥S−ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点(不含端点)，设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S−AB−C的平面角为θ3，则
A. θ1≤θ2≤θ3 B. θ3≤θ2≤θ1 C. θ1≤θ3≤θ2 D. θ2≤θ3≤θ1
【答案】D
【解析】设O为正方形ABCD的中心，M为AB中点，过E作BC的平行线EF，交CD于F，过O作ON垂直EF于N，连接SO，SN，OM，则SO垂直于底面ABCD，OM垂直于AB，
因此
从而
因为，所以即，选D.
5. (2018年全国I卷)已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为
A. B. C. D.
【答案】A
【解析】根据相互平行的直线与平面所成的角是相等的，
所以在正方体中，
平面与线所成的角是相等的，
所以平面与正方体的每条棱所在的直线所成角都是相等的，
同理平面也满足与正方体的每条棱所在的直线所成角都是相等，
要求截面面积最大，则截面的位置为夹在两个面与中间的，
且过棱的中点的正六边形，且边长为，
所以其面积为，故选A.
6. (2018年全国I卷)某圆柱的高为2，底面周长为16，其三视图如右图．圆柱表面上的点在正视图上的对应点为，圆柱表面上的点在左视图上的对应点为，则在此圆柱侧面上，从到的路径中，最短路径的长度为

A. B.
C. D. 2
【答案】B
【解析】根据圆柱的三视图以及其本身的特征，可以确定点M和点N分别在以圆柱的高为长方形的宽，圆柱底面圆周长的四分之一为长的长方形的对角线的端点处，所以所求的最短路径的长度为，故选B.
7. (2018年全国Ⅲ卷)设是同一个半径为4的球的球面上四点，为等边三角形且其面积为，则三棱锥体积的最大值为
A. B. C. D.
【答案】B
【解析】如图所示，

点M为三角形ABC的重心，E为AC中点，
当平面时，三棱锥体积最大
此时，

,
点M为三角形ABC的重心

中，有


故选B.
8. (2018年全国Ⅱ卷)在长方体中，，，则异面直线与所成角的余弦值为
A. B. C. D.
【答案】C
【解析】以D为坐标原点，DA,DC,DD1为x,y,z轴建立空间直角坐标系，则,所以,因为，所以异面直线与所成角的余弦值为，选C.
9. (2018年天津卷) 已知正方体的棱长为1，除面外，该正方体其余各面的中心分别为点E，F，G，H，M(如图)，则四棱锥的体积为__________.

【答案】
【解析】由题意可得，底面四边形为边长为的正方形，其面积，
顶点到底面四边形的距离为，
由四棱锥的体积公式可得：.
10. (2018年江苏卷)如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为________．

【答案】
【解析】由图可知，该多面体为两个全等正四棱锥的组合体，正四棱锥的高为1，底面正方形的边长等于，所以该多面体的体积为
11. (2018年全国Ⅱ卷) 已知圆锥的顶点为，母线，所成角的余弦值为，与圆锥底面所成角为45°，若的面积为，则该圆锥的侧面积为__________．
【答案】
【解析】先根据三角形面积公式求出母线长，再根据母线与底面所成角得底面半径，最后根据圆锥侧面积公式求结果.因为母线，所成角的余弦值为，所以母线，所成角的正弦值为，因为的面积为，设母线长为所以，因为与圆锥底面所成角为45°，所以底面半径为因此圆锥的侧面积为
1.【2017课标1，理7】某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为

A．10 B．12 C．14 D．16
【答案】B
【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成，如下图，则该几何体各面内只有两个相同的梯形，则这些梯形的面积之和为，故选B.

2.【2017课标II，理4】如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为( )
A． B． C． D．

【答案】B
【解析】由题意，该几何体是一个组合体，下半部分是一个底面半径为3，高为4的圆柱，其体积，上半部分是一个底面半径为3，高为6的圆柱的一半，其体积，故该组合体的体积．故选B．
3.【2017北京，理7】某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为

(A)3 (B)2 (C)2 (D)2
【答案】B
【解析】几何体是四棱锥，如图.

最长的棱长为补成的正方体的体对角线，即该四棱锥的最长棱的长度，故选B.
4.【2017山东，理13】由一个长方体和两个圆柱体构成的几何体的三视图如右图，则该几何体的体积为 .

【答案】
【解析】由三视图可知，长方体的长、宽、高分别为2，1，1，圆柱的高为1，底面圆半径为1，所以
.
5.【2017课标1，理16】如图，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形.沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥.当△ABC的边长变化时，所得三棱锥体积(单位：cm3)的最大值为_______.

【答案】
【解析】如下图，连接DO交BC于点G，设D，E，F重合于S点，正三角形的边长为x(x>0)，则 .
，
，
三棱锥的体积 .
设，x>0，则，
令，即，得，易知在处取得最大值.
∴.

【考点】简单几何体的体积
1、【2016高考新课标1卷】如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是( )
(A) (B) (C) (D)

【答案】A
【解析】该几何体直观图如图所示：

是一个球被切掉左上角的,设球的半径为,则,解得,所以它的表面积是的球面面积和三个扇形面积之和
故选A．
2.【2016高考新课标2】下图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( )

(A) (B) (C) (D)
【答案】C
【解析】由题意可知，圆柱的侧面积为，圆锥的侧面积为，圆柱的底面面积为，故该几何体的表面积为，故选C.
3.【2016年高考北京】某三棱锥的三视图如图所示，则该三棱锥的体积为()

A. B. C.D.
【答案】A
【解析】分析三视图可知，该几何体为一三棱锥，其体积，故选A.

4.【2016高考新课标3】如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为( )

(A) (B) (C)90 (D)81
【答案】B
【解析】由三视图该几何体是以侧视图为底面的斜四棱柱，所以该几何体的表面积
，故选B．
5.【2016高考山东】一个由半球和四棱锥组成的几何体，其三视图如图所示.则该几何体的体积为( )

(A) (B) (C) (D)
【答案】C
【解析】由三视图可知,上面是半径为的半球,体积为,下面是底面积为1,高为1的四棱锥,体积,故选C.