备战2024年高考总复习一轮（数学）第4章 三角函数、解三角形 第5节 函数y=Asin(ωx+φ)的图象及三角函数的应用课件PPT

这是一份备战2024年高考总复习一轮（数学）第4章 三角函数、解三角形 第5节 函数y=Asin(ωx+φ)的图象及三角函数的应用课件PPT，共38页。PPT课件主要包含了内容索引，强基础固本增分，研考点精准突破，答案C，答案D，答案A等内容，欢迎下载使用。
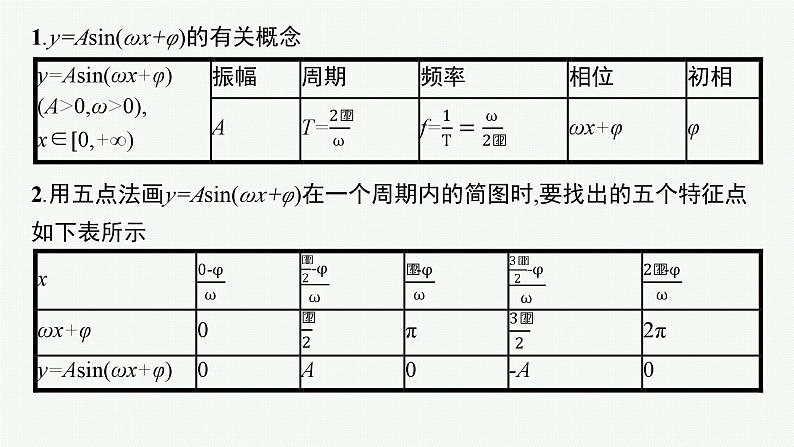
1.y=Asin(ωx+φ)的有关概念
2.用五点法画y=Asin(ωx+φ)在一个周期内的简图时,要找出的五个特征点如下表所示
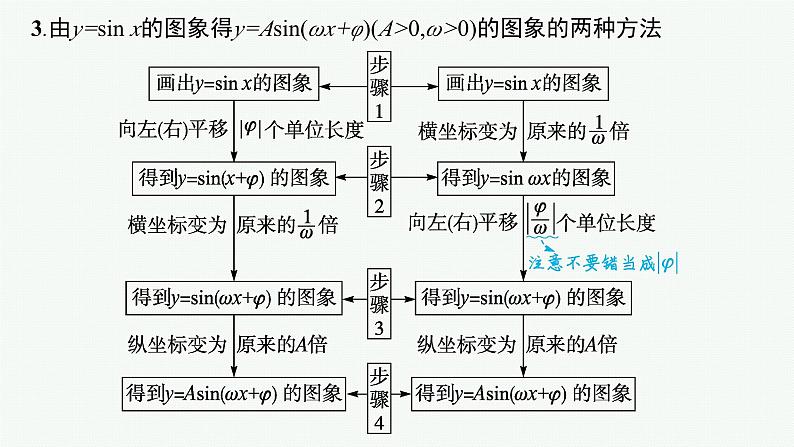
3.由y=sin x的图象得y=Asin(ωx+φ)(A>0,ω>0)的图象的两种方法
微点拨无论哪种变换,每一个变换总是针对自变量x而言的,即图象变换要看“自变量x”发生多大变化,而不是看角“ωx+φ”的变化.微思考先平移变换再周期变换和先周期变换再平移变换有什么联系与区别?
提示:两种变换方法都是针对x而言的,即x本身加减多少,而不是ωx加减多少.先平移变换(左右平移)再周期变换(伸缩变换),平移的量是|φ|个单位长度,而先周期变换(伸缩变换)再平移变换(左右平移),平移的量是 个单位长度.
常用结论1.函数y=Asin(ωx+φ)+k图象平移的规律:“左加右减,上加下减”.2.在正弦、余弦函数图象中,相邻的两个对称中心以及相邻的两条对称轴之间的距离均为 个周期.3.若直线x=a为正(余)弦曲线的对称轴,则正(余)弦函数一定在x=a处取得最值.
答案:(1)D　(2)B
规律方法 解决三角函数图象与性质的综合问题的关键是首先正确的将已知条件转化为三角函数解析式和图象,然后再根据数形结合思想研究函数的性质(单调性、奇偶性、对称性、周期性).
例4海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:
(1)已知该港口的水深与时间满足函数y=Acs(ωx+φ)+b(A>0,ω>0,b>0,-π