备战2024年高考数学大一轮复习（人教A版-理）第十三章 §13.3 绝对值不等式

这是一份备战2024年高考数学大一轮复习（人教A版-理）第十三章 §13.3 绝对值不等式，共9页。
§13.3　绝对值不等式
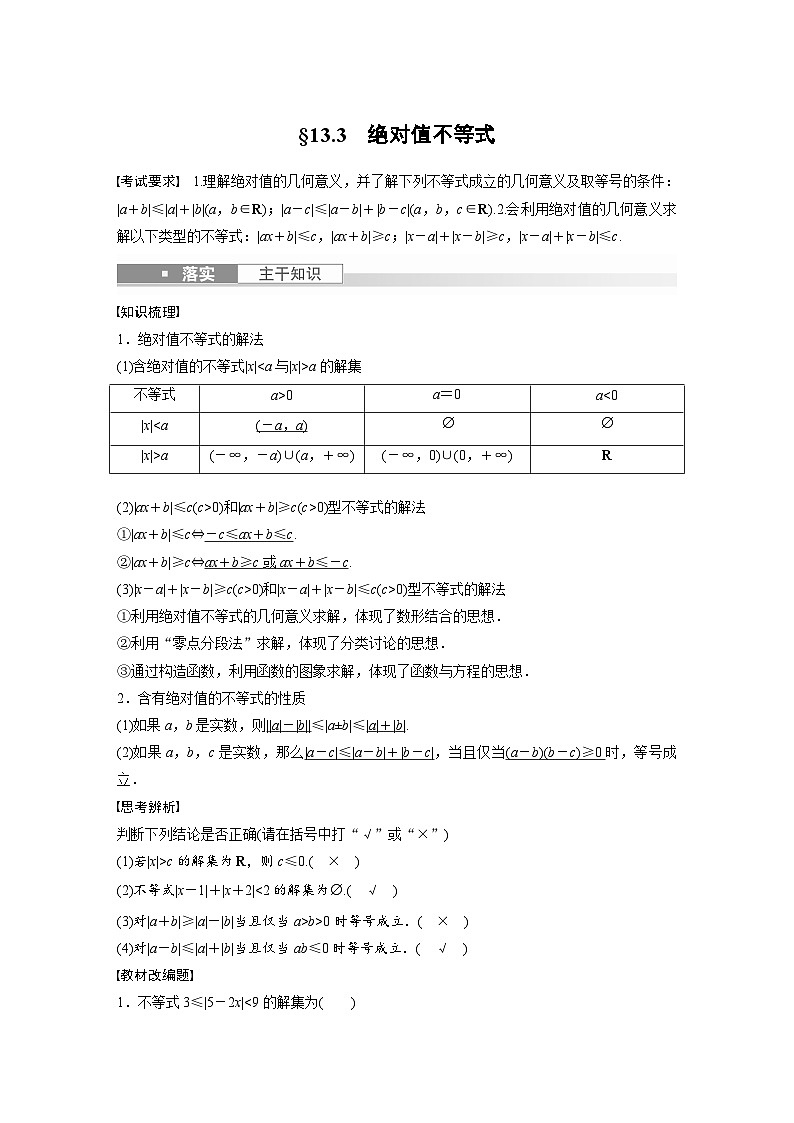
考试要求　1.理解绝对值的几何意义，并了解下列不等式成立的几何意义及取等号的条件：|a＋b|≤|a|＋|b|(a，b∈R)；|a－c|≤|a－b|＋|b－c|(a，b，c∈R).2.会利用绝对值的几何意义求解以下类型的不等式：|ax＋b|≤c，|ax＋b|≥c；|x－a|＋|x－b|≥c，|x－a|＋|x－b|≤c.

知识梳理
1．绝对值不等式的解法
(1)含绝对值的不等式|x|a的解集
不等式
a>0
a＝0
a0)和|ax＋b|≥c(c>0)型不等式的解法
①|ax＋b|≤c⇔－c≤ax＋b≤c.
②|ax＋b|≥c⇔ax＋b≥c或ax＋b≤－c.
(3)|x－a|＋|x－b|≥c(c>0)和|x－a|＋|x－b|≤c(c>0)型不等式的解法
①利用绝对值不等式的几何意义求解，体现了数形结合的思想．
②利用“零点分段法”求解，体现了分类讨论的思想．
③通过构造函数，利用函数的图象求解，体现了函数与方程的思想．
2．含有绝对值的不等式的性质
(1)如果a，b是实数，则||a|－|b||≤|a±b|≤|a|＋|b|.
(2)如果a，b，c是实数，那么|a－c|≤|a－b|＋|b－c|，当且仅当(a－b)(b－c)≥0时，等号成立．
思考辨析
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)若|x|>c的解集为R，则c≤0.(　×　)
(2)不等式|x－1|＋|x＋2|b>0时等号成立．(　×　)
(4)对|a－b|≤|a|＋|b|当且仅当ab≤0时等号成立．(　√　)
教材改编题
1．不等式3≤|5－2x|1的解集为(0，＋∞)．
(2)因为f(x)＋2≥4对∀x∈R都成立，
所以＋≥4恒成立，
只需min≥4即可，
由绝对值三角不等式知＋≥＝，当且仅当(x＋m)(x－2)≤0时等号成立，
所以≥4，解得m≥2或m≤－6.
故实数m的取值范围为(－∞，－6]∪[2，＋∞)．

题型三　绝对值不等式的综合应用
例3 设函数f(x)＝|2x＋1|＋|x－1|.
(1)画出y＝f(x)的图象；
(2)当x∈[0，＋∞)时，f(x)≤ax＋b，求a＋b的最小值．

解　(1)由题意得f(x)＝
则y＝f(x)的图象如图所示．

(2)由(1)知，y＝f(x)的图象与y轴交点的纵坐标为2，且各部分所在直线斜率的最大值为3，
故当且仅当a≥3且b≥2时，f(x)≤ax＋b在[0，＋∞)上恒成立，因此a＋b的最小值为5.
思维升华 (1)解决与绝对值有关的综合问题的关键是去掉绝对值，化为分段函数．
(2)数形结合是解决与绝对值有关的综合问题的常用方法．
跟踪训练3 (2023·成都联考)已知函数f(x)＝|x－2|－a|x＋1|.
(1)当a＝1时，求不等式f(x)m＋1恰有2个整数解，求实数m的取值范围．
解　(1)当a＝1时，f(x)＝|x－2|－|x＋1|，则不等式f(x)