

所属成套资源:新高考数学一轮复习课时讲练 (含解析)
新高考数学一轮复习课时讲练 第9章 第6讲 双曲线 (含解析)
展开
这是一份新高考数学一轮复习课时讲练 第9章 第6讲 双曲线 (含解析),共22页。试卷主要包含了双曲线的定义,双曲线中一些常用的结论,已知F是双曲线C,已知l是双曲线C等内容,欢迎下载使用。
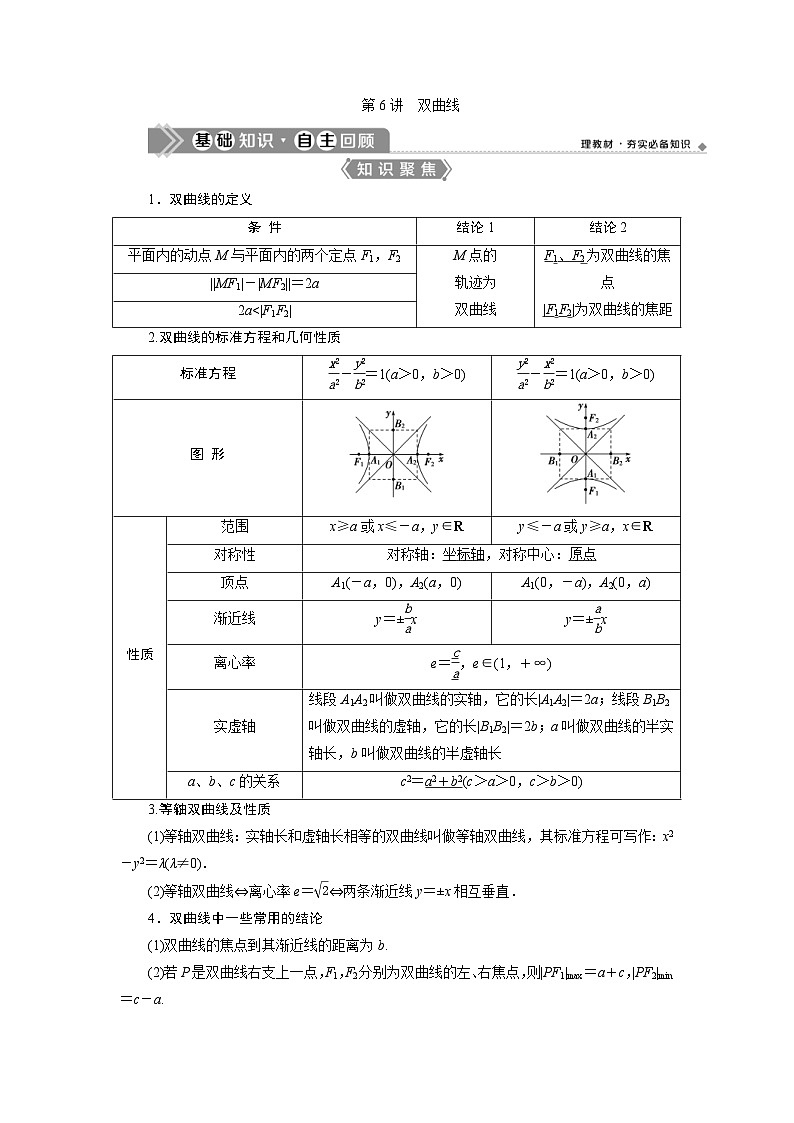
第6讲 双曲线
1.双曲线的定义
条 件
结论1
结论2
平面内的动点M与平面内的两个定点F1,F2
M点的
轨迹为
双曲线
F1、F2为双曲线的焦点
|F1F2|为双曲线的焦距
||MF1|-|MF2||=2a
2a0)表示焦点在x轴上的双曲线.( )
(4)等轴双曲线的渐近线互相垂直,离心率等于.( )
答案:(1)× (2)√ (3)× (4)√
[教材衍化]
1.(选修21P61A组T1改编)若双曲线-=1(a>0,b>0)的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为________.
解析:由题意知焦点到其渐近线的距离等于实轴长,双曲线的渐近线方程为±=0,即bx±ay=0,
所以2a==b.
又a2+b2=c2,所以5a2=c2.
所以e2==5,所以e=.
答案:
2.(选修21P62A组T6改编)经过点A(3,-1),且对称轴都在坐标轴上的等轴双曲线方程为________.
解析:设双曲线的方程为-=±1(a>0),
把点A(3,-1)代入,得a2=8(舍负),
故所求方程为-=1.
答案:-=1
3.(选修21P61练习T3改编)以椭圆+=1的焦点为顶点,顶点为焦点的双曲线方程为________.
解析:设要求的双曲线方程为-=1(a>0,b>0),由椭圆+=1,得焦点为(±1,0),顶点为(±2,0).所以双曲线的顶点为(±1,0),焦点为(±2,0).所以a=1,c=2,所以b2=c2-a2=3,所以双曲线标准方程为x2-=1.
答案:x2-=1
[易错纠偏]
(1)忽视双曲线的定义;
(2)忽视双曲线焦点的位置;
(3)忽视双曲线的渐近线与离心率的关系.
1.平面内到点F1(0,4),F2(0,-4)的距离之差等于6的点的轨迹是________.
解析:由|PF1|-|PF2|=6<|F1F2|=8,得a=3,又c=4,则b2=c2-a2=7,所以所求点的轨迹是双曲线-=1的下支.
答案:双曲线-=1的下支
2.坐标原点为对称中心,两坐标轴为对称轴的双曲线的一条渐近线的倾斜角为,则双曲线的离心率为________.
解析:若双曲线的焦点在x轴上,设双曲线的方程为-=1,则渐近线的方程为y=±x,由题意可得=tan =,b=a,可得c=2a,则e==2;若双曲线的焦点在y轴上,设双曲线的方程为-=1,则渐近线的方程为y=±x,由题意可得=tan =,a=b,可得c=a,则e=.综上可得e=2或e=.
答案:2或
3.若双曲线-=1(a>0,b>0)的一条渐近线经过点(3,-4),则此双曲线的离心率为________.
解析:由条件知y=-x过点(3,-4),所以=4,即3b=4a,所以9b2=16a2,所以9c2-9a2=16a2,所以25a2=9c2,所以e=.
答案:
双曲线的定义
(1)(2020·宁波高三质检)设双曲线x2-=1的两个焦点为F1,F2,P是双曲线上的一点,且|PF1|∶|PF2|=3∶4,则△PF1F2的面积等于( )
A.10 B.8
C.8 D.16
(2)(2020·温州八校联考)△ABC的顶点A(-5,0),B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是________.
【解析】 (1)依题意|F1F2|=6,|PF2|-|PF1|=2,因为|PF1|∶|PF2|=3∶4,所以|PF1|=6,|PF2|=8,所以等腰三角形PF1F2的面积S=×8× =8.
(2)如图,△ABC与内切圆的切点分别为G,E,F.
|AG|=|AE|=8,|BF|=|BG|=2,|CE|=|CF|,
所以|CA|-|CB|=8-2=6.
根据双曲线的定义,所求轨迹是以A,B为焦点,实轴长为6的双曲线的右支,方程为-=1(x>3).
【答案】 (1)C (2)-=1(x>3)
(变条件)若本例(1)中“|PF1|∶|PF2|=3∶4”变为“PF1⊥PF2”,其他条件不变,如何求解.
解:设|PF1|=m,|PF2|=n,则
解得mn=16,所以S△PF1F2=mn=8.
双曲线定义的应用规律
类型
解读
求方程
由题目条件判断出动点轨迹是双曲线,由双曲线的定义,确定2a,2b或2c的值,从而求出a2,b2的值,写出双曲线方程
解焦点三角形
利用双曲线上点M与两焦点的距离的差||MF1|-|MF2||=2a(其中2a0).
由已知条件可得解得
所以双曲线的标准方程为-y2=1.
双曲线的几何性质(高频考点)
双曲线的几何性质及应用,是高考命题的热点,多以选择题或填空题的形式呈现,试题多为容易题或中档题.主要命题角度有:
(1)求双曲线的焦点(距)、实、虚轴长;
(2)求双曲线的渐近线方程;
(3)求双曲线的离心率(或范围).
角度一 求双曲线的焦点(距)、实、虚轴长
(2020·义乌模拟)已知离心率为的双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1,F2,M是双曲线C的一条渐近线上的点,且OM⊥MF2,O为坐标原点,若S△OMF2=16,则双曲线的实轴长是( )
A.32 B.16
C.84 D.4
【解析】 由题意知F2(c,0),不妨令点M在渐近线y=x上,由题意可知|F2M|==b,所以|OM|==a.由S△OMF2=16,可得ab=16,即ab=32,又a2+b2=c2,=,所以a=8,b=4,c=4,所以双曲线C的实轴长为16.故选B.
【答案】 B
角度二 求双曲线的渐近线方程
已知F1,F2是双曲线C:-=1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2最小内角的大小为30°,则双曲线C的渐近线方程是( )
A.x±y=0 B.x±y=0
C.x±2y=0 D.2x±y=0
【解析】 由题意,不妨设|PF1|>|PF2|,则根据双曲线的定义得,|PF1|-|PF2|=2a,
又|PF1|+|PF2|=6a,
解得|PF1|=4a,|PF2|=2a.
在△PF1F2中,|F1F2|=2c,而c>a,
所以有|PF2|<|F1F2|,
所以∠PF1F2=30°,所以(2a)2=(2c)2+(4a)2-2·2c·4acos 30°,得c=a,所以b==a,
所以双曲线的渐近线方程为y=±x=±x,
即x±y=0.
【答案】 A
角度三 求双曲线的离心率(或范围)
(1)(2019·高考浙江卷)渐近线方程为x±y=0的双曲线的离心率是( )
A. B.1
C. D.2
(2)已知双曲线-=1(a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P使=,则该双曲线的离心率的取值范围是________.
【解析】 (1)因为双曲线的渐近线方程为x±y=0,所以无论双曲线的焦点在x轴上还是在y轴上,都满足a=b,所以c=a,所以双曲线的离心率e==.故选C.
(2)在△PF1F2中,由正弦定理知=,又=,所以=,所以点P在双曲线右支上,设P(x0,y0),如图,
又因为|PF1|-|PF2|=2a,所以|PF2|=.由双曲线的几何性质知|PF2|>c-a,则>c-a,即e2-2e-10)的焦距为2c(c>0),则C(-a,0),F(-c,0).
由双曲线和圆的对称性知,点A与点B关于x轴对称,则∠ACO=∠BCO=∠ACB=×120°=60°.
因为|OA|=|OC|=a,
所以△ACO为等边三角形,
所以∠AOC=60°.
因为FA与圆O相切于点A,所以OA⊥FA,
在Rt△AOF中,∠AFO=90°-∠AOF=90°-60°=30°,所以|OF|=2|OA|,即c=2a,
所以b= = =a,
故双曲线-=1(a>0,b>0)的渐近线方程为
y=±x,即y=±x.
2.(2020·绍兴诸暨高考模拟)设双曲线-=1(a>0,b>0)的左,右焦点分别是F1,F2,点P在双曲线上,且满足∠PF2F1=2∠PF1F2=60°,则此双曲线的离心率等于( )
A.2-2 B.
C.+1 D.2+2
解析:选C.设双曲线的焦距长为2c,
因为点P为双曲线上一点,且∠PF1F2=30°,∠PF2F1=60°,
所以P在右支上,∠F2PF1=90°,
即PF1⊥PF2,|PF1|=2csin 60°=c,
|PF2|=2ccos 60°=c,
所以由双曲线的定义可得|PF1|-|PF2|=(-1)c=2a,所以e===+1.
故选C.
3.(2020·嘉兴一中高考适应性考试)若双曲线-=1(a>0,b>0)的右焦点到渐近线的距离等于焦距的倍,则双曲线的离心率为________,如果双曲线上存在一点P到双曲线的左右焦点的距离之差为4,则双曲线的虚轴长为________.
解析:因为右焦点到渐近线的距离为b,若右焦点到渐近线的距离等于焦距的倍,
所以b=·2c=c,
平方得b2=c2=c2-a2,即a2=c2,
则c=2a,则离心率e==2,
因为双曲线上存在一点P到双曲线的左右焦点的距离之差为4,
所以2a=4,则a=2,从而b==2.
答案:2 4
直线与双曲线的位置关系
已知中心在原点的双曲线C的右焦点为(2,0),实轴长为2.
(1)求双曲线C的方程;
(2)若直线l:y=kx+与双曲线C左支交于A,B两点,求k的取值范围.
【解】 (1)设双曲线C的方程为-=1(a>0,b>0).
由已知得,a=,c=2,再由a2+b2=c2,得b2=1,
所以双曲线C的方程为-y2=1.
(2)设A(xA,yA),B(xB,yB),
将y=kx+代入-y2=1,
得(1-3k2)x2-6kx-9=0.
由题意知
所以k的取值范围为.
(变问法)在本例(2)的条件下,线段AB的垂直平分线l0与y轴交于M(0,m),求m的取值范围.
解:由(2)得:xA+xB=,
所以yA+yB=(kxA+)+(kxB+)
=k(xA+xB)+2=.
所以AB的中点P的坐标为.
设直线l0的方程为:y=-x+m,
将P点坐标代入直线l0的方程,得m=.
因为0,b>0)的离心率为,则其渐近线方程为( )
A.y=±2x B.y=±x
C.y=±x D.y=±x
解析:选B.由条件e=,即=,得==1+=3,所以=±,所以双曲线的渐近线方程为y=±x.故选B.
2.已知双曲线-=1(a>0,b>0)的一条渐近线为y=kx(k>0),离心率e=k,则双曲线的方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
解析:选C.由已知得
所以a2=4b2.所以双曲线的方程为-=1.
3.(2020·杭州学军中学高三质检)双曲线M:x2-=1的左、右焦点分别为F1,F2,记|F1F2|=2c,以坐标原点O为圆心,c为半径的圆与曲线M在第一象限的交点为P,若|PF1|=c+2,则点P的横坐标为( )
A. B.
C. D.
解析:选A.由点P在双曲线的第一象限可得|PF1|-|PF2|=2,则|PF2|=|PF1|-2=c,又|OP|=c,∠F1PF2=90°,由勾股定理可得(c+2)2+c2=(2c)2,解得c=1+.易知△POF2为等边三角形,则xP==,选项A正确.
4.(2020·杭州中学高三月考)已知F1,F2分别是双曲线C:-=1(a>0,b>0)的左、右焦点,若F2关于渐近线的对称点恰落在以F1为圆心,OF1为半径的圆上,则双曲线C的离心率为( )
A. B.3
C. D.2
解析:选D.由题意,F1(-c,0),F2(c,0),一条渐近线方程为y=x,则F2到渐近线的距离为=b.
设F2关于渐近线的对称点为M,F2M与渐近线交于点A,所以|MF2|=2b,A为F2M的中点,又O是F1F2的中点,所以OA∥F1M,所以∠F1MF2为直角,
所以△MF1F2为直角三角形,
所以由勾股定理得4c2=c2+4b2,
所以3c2=4(c2-a2),所以c2=4a2,
所以c=2a,所以e=2.
故选D.
5.已知F是双曲线C:x2-=1的右焦点,P是C上一点,且PF与x轴垂直,点A的坐标是(1,3),则△APF的面积为( )
A. B.
C. D.
解析:选D.法一:由题可知,双曲线的右焦点为F(2,0),当x=2时,代入双曲线C的方程,得4-=1,解得y=±3,不妨取点P(2,3),因为点A(1,3),所以AP∥x轴,又PF⊥x轴,所以AP⊥PF,所以S△APF=|PF|·|AP|=×3×1=.故选D.
法二:由题可知,双曲线的右焦点为F(2,0),当x=2时,代入双曲线C的方程,得4-=1,解得y=±3,不妨取点P(2,3),因为点A(1,3),所以=(1,0),=(0,-3),所以·=0,所以AP⊥PF,所以S△APF=|PF|·|AP|=×3×1=.故选D.
6.(2020·浙江高中学科基础测试)已知双曲线-=1(a>0,b>0)与抛物线y2=20x有一个公共的焦点F,且两曲线的一个交点为P,若|PF|=17,则双曲线的离心率为( )
A. B.
C. D.
解析:选B.由题意知F(5,0),不妨设P点在x轴的上方,由|PF|=17知点P的横坐标为17-5=12,则其纵坐标为=4,设双曲线的另一个焦点为F1(-5,0),则|PF1|==23,所以2a=|PF1|-|PF|=23-17=6,所以a=3,所以e==,故选B.
7.(2020·宁波市余姚中学高三期中)已知曲线+=1,当曲线表示焦点在y轴上的椭圆时k的取值范围是________;当曲线表示双曲线时k的取值范围是________.
解析:当曲线表示焦点在y轴上的椭圆时,k2-k>2,
所以k<-1或k>2;
当曲线表示双曲线时,k2-k<0,
所以0<k<1.
答案:k<-1或k>2 0<k<1
8.(2020·金华十校联考)已知l是双曲线C:-=1的一条渐近线,P是l上的一点,F1,F2是C的两个焦点,若·=0,则P到x轴的距离为________.
解析:F1(-,0),F2(,0),不妨设l的方程为y=x,则可设P(x0,x0),由·=(--x0,-x0)·(-x0,-x0)=3x-6=0,得x0=±,故P到x轴的距离为|x0|=2.
答案:2
9.(2020·瑞安四校联考)设双曲线-=1(a>0,b>0)的两条渐近线与直线x=分别交于A,B两点,F为该双曲线的右焦点.若60°
相关试卷
这是一份(新高考)高考数学一轮复习讲练测第8章§8.6双曲线(含解析),共18页。
这是一份新高考数学一轮复习课时讲练 第6章 第5讲 数列的综合应用 (含解析),共19页。
这是一份新高考数学一轮复习课时讲练 第6章 第4讲 数列求和 (含解析),共17页。试卷主要包含了基本数列求和方法,一些常见数列的前n项和公式,数列求和的常用方法,已知数列{an}满足等内容,欢迎下载使用。










