浙江宁波市2023年各地区中考数学模拟（一模）试题按题型难易度分层分类汇编（8套）-02填空题（提升题）

这是一份浙江宁波市2023年各地区中考数学模拟（一模）试题按题型难易度分层分类汇编（8套）-02填空题（提升题），共23页。试卷主要包含了称为点P的“和差点”等内容，欢迎下载使用。

浙江宁波市2023年各地区中考数学模拟（一模）试题按题型难易度分层分类汇编（8套）-02填空题（提升题）
一．反比例函数系数k的几何意义（共5小题）
1．（2023•余姚市一模）如图，在平面直角坐标系中，Rt△AOB斜边上的中点C在y轴正半轴上，M为AC的中点．反比例函数的图象经过点A，M，延长MO交函数在第四象限的图象于点N．反比例函数的图象经过点B，连结BN．若△BMN的面积为18，则m﹣n的值为 　 　．

2．（2023•镇海区一模）在平面直角坐标系中，对于任意一个不在坐标轴上的点P（x，y），我们把点P′（x+y，x﹣y）称为点P的“和差点”．若直线y＝﹣2x+1上有两个点A和B，它们的和差点A'和B'均在反比例函数y＝上，则△OAB的面积为 　 　．
3．（2023•江北区一模）如图，菱形ABCO的顶点A与对角线交点D都在反比例函数的图象上，对角线AC交y轴于点E，CE＝2DE，且△ADB的面积为15，则k＝　 　；延长BA交x轴于点F，则点F的坐标为 　 　．

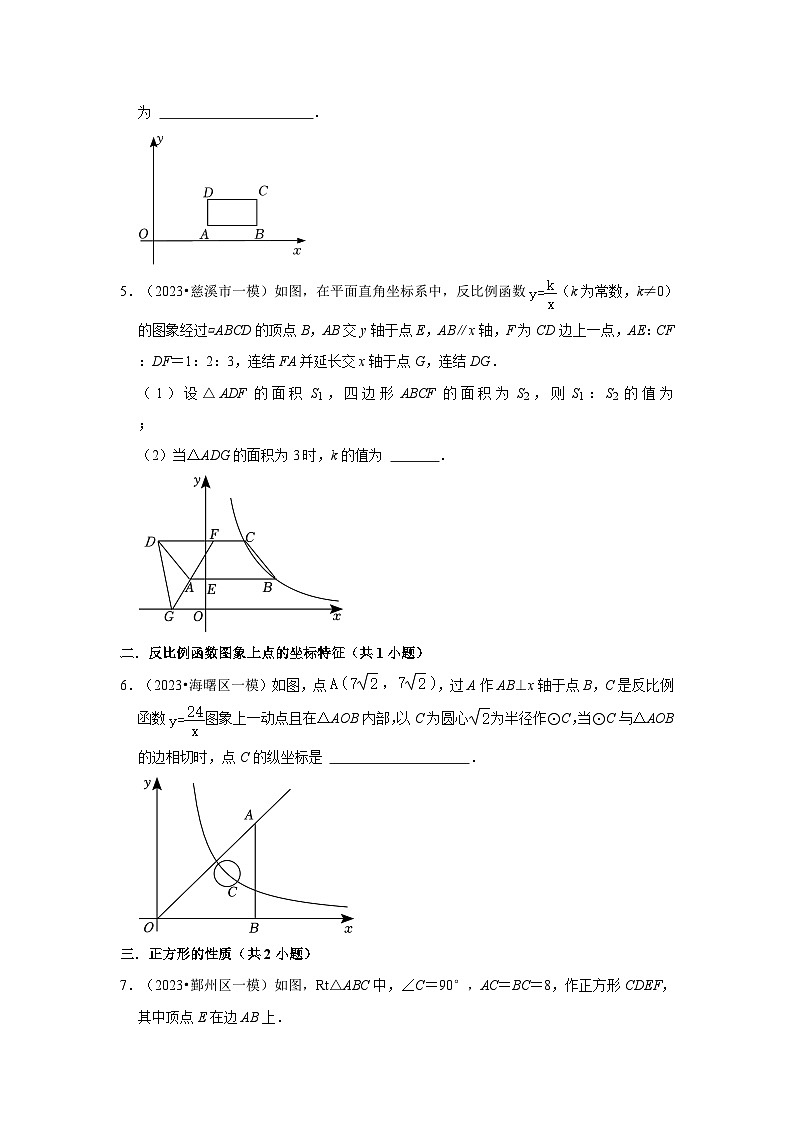
4．（2023•北仑区一模）定义：若一个矩形中，一组对边的两个三等分点在同一个反比例函数的图象上，则称这个矩形为“奇特矩形”．如图，在直角坐标系中，矩形ABCD是第一象限内的一个“奇特矩形”．且点A（4，1），B（7，1），则矩形ABCD的面积为 　 　．

5．（2023•慈溪市一模）如图，在平面直角坐标系中，反比例函数（k为常数，k≠0）的图象经过▱ABCD的顶点B，AB交y轴于点E，AB∥x轴，F为CD边上一点，AE：CF：DF＝1：2：3，连结FA并延长交x轴于点G，连结DG．
（1）设△ADF的面积S1，四边形ABCF的面积为S2，则S1：S2的值为 　 　；
（2）当△ADG的面积为3时，k的值为 　 　．

二．反比例函数图象上点的坐标特征（共1小题）
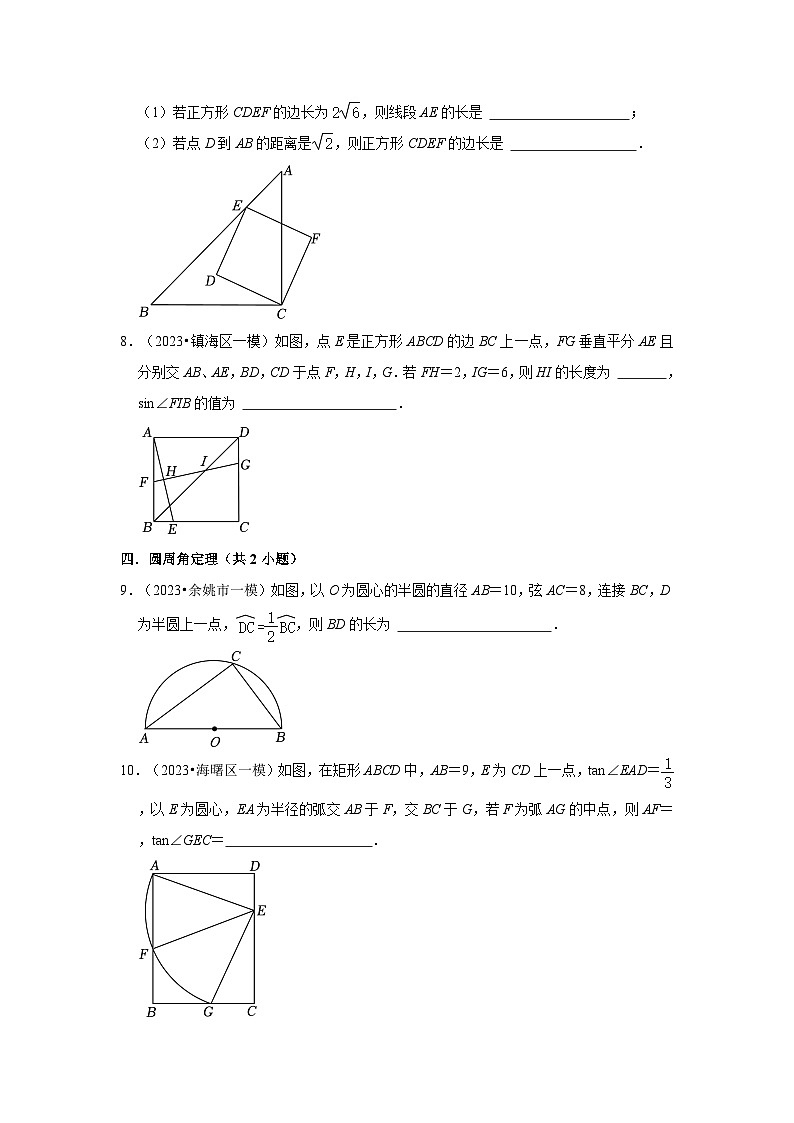
6．（2023•海曙区一模）如图，点，过A作AB⊥x轴于点B，C是反比例函数图象上一动点且在△AOB内部，以C为圆心为半径作⊙C，当⊙C与△AOB的边相切时，点C的纵坐标是 　 　．

三．正方形的性质（共2小题）
7．（2023•鄞州区一模）如图，Rt△ABC中，∠C＝90°，AC＝BC＝8，作正方形CDEF，其中顶点E在边AB上．
（1）若正方形CDEF的边长为，则线段AE的长是 　 　；
（2）若点D到AB的距离是，则正方形CDEF的边长是 　 　．

8．（2023•镇海区一模）如图，点E是正方形ABCD的边BC上一点，FG垂直平分AE且分别交AB、AE，BD，CD于点F，H，I，G．若FH＝2，IG＝6，则HI的长度为 　 　，sin∠FIB的值为 　 　．

四．圆周角定理（共2小题）
9．（2023•余姚市一模）如图，以O为圆心的半圆的直径AB＝10，弦AC＝8，连接BC，D为半圆上一点，，则BD的长为 　 　．

10．（2023•海曙区一模）如图，在矩形ABCD中，AB＝9，E为CD上一点，tan∠EAD＝，以E为圆心，EA为半径的弧交AB于F，交BC于G，若F为弧AG的中点，则AF＝　 　，tan∠GEC＝　 　．

五．相似三角形的判定与性质（共1小题）
11．（2023•北仑区一模）如图，一张矩形纸片ABCD中，（m为常数）．将矩形纸片ABCD沿EF折叠，使点A落在BC边上的点H处，点D的对应点为点M，CD与HM交于点P．当点H落在BC的中点时，且，则m＝　 　．


浙江宁波市2023年各地区中考数学模拟（一模）试题按题型难易度分层分类汇编（8套）-02填空题（提升题）
参考答案与试题解析
一．反比例函数系数k的几何意义（共5小题）
1．（2023•余姚市一模）如图，在平面直角坐标系中，Rt△AOB斜边上的中点C在y轴正半轴上，M为AC的中点．反比例函数的图象经过点A，M，延长MO交函数在第四象限的图象于点N．反比例函数的图象经过点B，连结BN．若△BMN的面积为18，则m﹣n的值为 　﹣24　．

【答案】﹣24．
【解答】解：作BE⊥y轴于E，AD⊥x轴于D，
∵M，N关于O对称，则MO＝NO，
∵△BMN的面积为18，
∴S△BMO＝9，
∵点M为AC的中点，
∴MC＝AC＝BC，
∴S△BOM＝3S△COM，
∴S△MOC＝3，
∴S△AOC＝S△BOC＝6，
∵C是AB的中点，
∴AC＝BC，
∵∠ADC＝∠BEC＝90°，∠BCE＝∠ACG，
∴△ACD≌△BCE（AAS），
∴S△ACD＝S△BCE，
即S△AOC﹣S△AOD＝S△BOE﹣S△BOC，
∵S△AOD＝，S△BOE＝，
∴，
∴m﹣n＝﹣24，
故答案为：﹣24．

2．（2023•镇海区一模）在平面直角坐标系中，对于任意一个不在坐标轴上的点P（x，y），我们把点P′（x+y，x﹣y）称为点P的“和差点”．若直线y＝﹣2x+1上有两个点A和B，它们的和差点A'和B'均在反比例函数y＝上，则△OAB的面积为 　　．
【答案】．
【解答】解：设A（a，﹣2a+1），则A′（﹣a+1，3a﹣1），
∵点A′在反比例函数y＝上，
∴（﹣a+1）（3a﹣1）＝﹣3，
整理得3a2﹣4a﹣2＝0，
∴a1+a2＝，a1a2＝﹣，
∴a2﹣a1＝＝＝，
在直线y＝﹣2x+1中，令x＝0，则y＝1，
∴D（0，1），
∴OD＝1，
∴S△OAB＝S△AOD+S△BOD＝＝．
故答案为：．

3．（2023•江北区一模）如图，菱形ABCO的顶点A与对角线交点D都在反比例函数的图象上，对角线AC交y轴于点E，CE＝2DE，且△ADB的面积为15，则k＝　8　；延长BA交x轴于点F，则点F的坐标为 　　．

【答案】8，．
【解答】解：延长DA交x轴于点M，

设DE＝a，则CE＝2a，CD＝AD＝3a，
∵ED＝a，
∴AM＝a，
∴Rt△MOE中，OD⊥EM，OD2＝ED⋅DM，
∴OD＝2a，
∵，
∴，
∴
过D作DN⊥y轴，则，
即ON＝2DN，
∵，
∴D（2，4），即k＝8．
∵D（2，4），
∴B（4，8），过点A作AH⊥ND于H，
∵∠OND＝∠H＝90°，
∠EDN+∠NDO＝90°，∠NDO+∠HDA＝90°，
∴∠NDO＝∠HDA，
∴△DHA∽△OND，
∵，
∴DH＝6，AH＝3，
∴A（8，1），
∴，
∴．
4．（2023•北仑区一模）定义：若一个矩形中，一组对边的两个三等分点在同一个反比例函数的图象上，则称这个矩形为“奇特矩形”．如图，在直角坐标系中，矩形ABCD是第一象限内的一个“奇特矩形”．且点A（4，1），B（7，1），则矩形ABCD的面积为 　或27　．

【答案】或27．
【解答】解：当反比例函数的图象经过AB、CD上的点时，
设BC＝n，
∵点A（4，1），B（7，1），
∴点（5，1+n）和点（6，1）在反比例函数的图象上，
∴5（1+n）＝6×1，
解得n＝；
当反比例函数的图象经过AD、BC上的点时，
设BC＝n，
∵点A（4，1），B（7，1），
∴点（4，1+n）和点（7，1+n）在反比例函数的图象上，
∴4（1+n）＝7（1+n），
解得n＝9，
∴BC的长为或9，
∵点A（4，1），B（7，1），
∴AB＝7﹣4＝3，
∴矩形的面积为或27．
故答案为：或27．
5．（2023•慈溪市一模）如图，在平面直角坐标系中，反比例函数（k为常数，k≠0）的图象经过▱ABCD的顶点B，AB交y轴于点E，AB∥x轴，F为CD边上一点，AE：CF：DF＝1：2：3，连结FA并延长交x轴于点G，连结DG．
（1）设△ADF的面积S1，四边形ABCF的面积为S2，则S1：S2的值为 　　；
（2）当△ADG的面积为3时，k的值为 　8　．

【答案】（1）；（2）8．
【解答】解：（1）设：每一份为a，
∵AE：CF：DF＝1：2：3，
∴AE＝a，CF＝2a，DF＝3a，
∵四边形ABCD是平行四边形，
∴AB＝CD＝5a，
设AB和CD之间的距离为h，
∴S1＝，S2＝（2a+5a）•h＝，
∴S1：S2＝＝；
故答案为：．
（2）如图，设点D到GF的距离为h1，点B到AF的距离为h2，
连接BF、GE、GB、OB，

∵DF＝3a，AB＝5a，
∴S△ADF：S△ABF＝3：5，即h1：h2＝3：5，
∴S△AGD：S△AGB＝3：5，
∵S△AGD＝3，
∴S△AGB＝5，
∵AE：BE＝1：4，
∴S△BEG＝4，
∴S△BEO＝4，
∴＝8，
∴k＝±8．
∵反比例函数在一、三象限，
∴k＝8．
故答案为：8．
二．反比例函数图象上点的坐标特征（共1小题）
6．（2023•海曙区一模）如图，点，过A作AB⊥x轴于点B，C是反比例函数图象上一动点且在△AOB内部，以C为圆心为半径作⊙C，当⊙C与△AOB的边相切时，点C的纵坐标是 　2或4　．

【答案】2或4．
【解答】解：（1）∵点A（7，7），过A作AB⊥x轴于点B，
∴OB＝AB＝7，∠ABO＝90°，
∴∠AOB＝∠OAB＝45°，
设直线OA的解析式为y＝kx，
∴7＝7k，
解得k＝1，
∴直线OA的解析式为y＝x，
①如图，当⊙C与OA相切时，
设C（m，n），过点C作CE⊥OA于E，过点C作CF∥x轴，交OA于点F，

∵⊙C的半径为，
∴CE＝，∠CEF＝90°，∠EFC＝∠AOB＝45°，
∴∠ECF＝90°﹣∠EFC＝45°＝∠EFC，
∴EF＝EC＝，
∴FC＝＝＝2，
∵点F（m﹣2，n）在直线OA：y＝x图象上，点C（m，n）在反比例函数y＝图象上，
∴，
解得或（不符合题，舍去），
此时点C的纵坐标为4；
②如图，当⊙C与AB相切，
设C（m，7），过点C作CM⊥AB于点M，

∵⊙C的半径为，
∴CM＝，
∵点A（7，7），AB上x轴，
∴m＝7﹣＝6，
∵点C（m1，n1）在反比例函数y＝图象上，
∴6n1＝2，
∴此时点C的纵坐标为2；
③当x＝7时，y＝＝＝，
∵当0＜x≤7时，y＝的函数值随x的增大而减小，
∴当x＝7时，y有最小值＞，
∴⊙C与△AOB的边OB不可能相切．
综上，点C的纵坐标为2或4．
故答案为：2或4．
三．正方形的性质（共2小题）
7．（2023•鄞州区一模）如图，Rt△ABC中，∠C＝90°，AC＝BC＝8，作正方形CDEF，其中顶点E在边AB上．
（1）若正方形CDEF的边长为，则线段AE的长是 　　；
（2）若点D到AB的距离是，则正方形CDEF的边长是 　　．

【答案】（1）或4+4；
（2）．
【解答】解：（1）连接CE，过点E作EH⊥AC于点H，如图所示：
则∠AHE＝90°，
在正方形CDEF中，CD＝DE＝，∠CDE＝90°，
根据勾股定理，得CE＝＝，
在Rt△ABC中，∠C＝90°，
∴∠A＝∠B＝45°，
∴∠AEH＝45°，
∴AH＝EH，
设AH＝EH＝x，
∵AC＝BC＝8，
∴CH＝8﹣x，
在Rt△EHC中，根据勾股定理，得，
解得x1＝（舍去），x2＝4﹣，
∴AH＝EH＝4﹣，
在Rt△AEH中，根据勾股定理，得AE＝＝，
当点E靠近点B的位置，同法可得AE＝4+4．
故答案为：或4+4；
（2）过点D作DM⊥AB于点M，连接BD，AF，过点F作FN⊥AB于点N，如图所示：
则∠DME＝∠FNE＝90°，
∴∠MDE+∠MED＝90°，
在正方形DCEF中，∠DEF＝90°，DE＝EF，
∴∠MED+∠FEN＝90°，
∴∠MDE＝∠FEN，
在△MDE和△NEF中，
，
∴△MDE≌△NEF（AAS），
∴EN＝DM，ME＝NF，
在Rt△ABC中，BC＝AC，∠ACB＝90°，
在正方形EDCF中，∠DCF＝90°，CD＝CF，
∴∠BCD＝∠ACF，
在△BCD和△ACF中，
，
∴△BCD≌△ACF（SAS），
∴BD＝AF，∠CAF＝∠CBD，
∵∠ABC+∠BAC＝90°，
∴∠MBD+∠DBC+∠BAC＝90°，
∴∠MBD+∠CAF+∠BAC＝90°，
即∠MBD+∠BAF＝90°，
∵∠MBD+∠MDB＝90°，
∴∠MDB＝∠BAF，
在△BMD和△FNA中，
，
∴△BMD≌△FNA（AAS），
∴BM＝NF，MD＝NA，
∴BM＝ME，EN＝NA＝MD，
∵点D到AB的距离是，
∴EN＝NA＝，
在Rt△ABC中，AC＝BC＝8，∠ACB＝90°，
根据勾股定理，得AB＝＝，
∴BM+ME＝﹣﹣＝6，
∴ME＝3，
在Rt△MDE中，根据勾股定理，DE＝＝2，
∴正方形CDEF的边长是2，
故答案为：2．


8．（2023•镇海区一模）如图，点E是正方形ABCD的边BC上一点，FG垂直平分AE且分别交AB、AE，BD，CD于点F，H，I，G．若FH＝2，IG＝6，则HI的长度为 　8　，sin∠FIB的值为 　　．

【答案】8，．
【解答】解：过点G作GM⊥AB于点M，连接IA，IE，IC，如图，
∵FG垂直平分AE，
∴∠AHF＝90°，AH＝EH，AI＝EI，
∴∠BAE+∠AFH＝90°，
∵四边形ABCD是正方形，
∴∠ABC＝∠ADC＝∠BAD＝90°，AB＝AD＝BC，
∴∠BAE+∠AEB＝90°，
∴∠AEB＝∠AFH，
即∠AEB＝∠GFM，
∵GM⊥AB，
∴∠AMG＝∠GMF＝90°，
∴四边形ADGM是矩形，
∴AD＝MG＝AB，
在△ABE和△GMF中，

∴△ABE≌△GMF（AAS），
∴AE＝GF，
∵BD是正方形ABCD的对角线，
∴∠ABI＝∠CBI＝45°，
在△ABI和△CBI中，

∴△ABI≌△CBI（SAS），
∴AI＝CI，∠IAB＝∠ICB，
∴IE＝IC，
∴∠IEC＝∠ICE，
∴∠IEC＝∠IAB，
∵∠IEC+∠IEB＝180°，
∴∠IAB+∠IEB＝180°，
∴∠AIE＝360°﹣∠ABE﹣（∠IAB+∠IEB）＝360°﹣90°﹣180°＝90°，
∴△IAE是等腰直角三角形，
∵IH⊥AE，
∴HI＝HA＝HN＝AE＝GF＝FH+IG，
∵FH＝2，IG＝6，
∴HI＝2+6＝8；
设AE，BD交于点N，
∵∠AHF＝∠ABE＝90°，
∠FAH＝∠EAB，
∴△AFH∽△AEB，
∴，
∴，
∴AB＝4BE，
∴AD＝4BE，
∵AD∥BE，
∴△ADN∽△EBN，
∴，
∴AN＝4EN，
∵AN+EN＝AE，
∴4EN+EN＝16，
∴EN＝，
∴NH＝EH﹣EN＝8﹣＝，
∴NI＝＝，
∴sin∠FIB＝sin∠EIH＝＝．
故答案为：8，．

四．圆周角定理（共2小题）
9．（2023•余姚市一模）如图，以O为圆心的半圆的直径AB＝10，弦AC＝8，连接BC，D为半圆上一点，，则BD的长为 　或　．

【答案】BD的长为或．
【解答】解：分两种情况：
①如图1，当点D在上时，连接BD，OD，OD交⊙O于点D，
∵，
∴OD⊥BC，
∴CE＝BE，
∵OA＝OB＝AB＝×10＝5，
∴OE是△ACB的中位线，
∴OE＝AC，
∵AC＝8，
∴OE＝4，
∵OD＝5，
∴DE＝5﹣4＝1，
∵AB是⊙O的直径，
∴∠ACB＝90°，
由勾股定理得：BC＝＝＝6，
∴BE＝BC＝3，
在Rt△BDE中，由勾股定理得：BD＝＝＝；
②如图2，当点D在上时，连接BD，CD，过点C作CF⊥BD于F，
由①知：CD＝，
∵＝，
∴∠A＝∠D，
∵cosA＝cosD，
∴＝，即＝，
∴DF＝，
同理得：CF＝，
在Rt△BCF中，由勾股定理得：BF＝＝＝，
∴BD＝DF+BF＝+＝．
综上，BD的长为或．
故答案为：或．


10．（2023•海曙区一模）如图，在矩形ABCD中，AB＝9，E为CD上一点，tan∠EAD＝，以E为圆心，EA为半径的弧交AB于F，交BC于G，若F为弧AG的中点，则AF＝　5　，tan∠GEC＝　　．

【答案】5，．
【解答】解：过E点作EH⊥AF于H点，连接AG、FG，如图，
∵四边形ABCD为矩形，
∴∠B＝∠C＝∠D＝∠BAD＝90°，
在Rt△ADE中，∵tan∠EAD＝＝，
∴设DE＝x，AD＝3x，
∵∠AHE＝∠HAD＝∠D＝90°，
∴四边形ADEH为矩形，
∴AH＝DE＝x，AD∥AE，
∴∠DAE＝∠HEA，
∵EH⊥AF，
∴AH＝FH＝x，∠HEA＝∠HEF，
∵F为弧AG的中点，
∴FG＝FA＝2x，∠AEF＝∠GEF，
∵∠FAG＝∠GEF＝∠AEF，
∴∠FAG＝∠EAD，
在Rt△ABG中，∵tan∠BAG＝＝，
∴BG＝AB＝×9＝3，
在Rt△BFG中，∵BF＝9﹣2x，FG＝2x，BG＝3，
∴（9﹣2x）2+32＝（2x）2，
解得x＝，
∴AF＝5，DE＝，AD＝，
∴CG＝BC﹣BG＝，CE＝CD﹣DE＝，
在Rt△CGE中，tan∠GEC＝＝．
故答案为：5，．

五．相似三角形的判定与性质（共1小题）
11．（2023•北仑区一模）如图，一张矩形纸片ABCD中，（m为常数）．将矩形纸片ABCD沿EF折叠，使点A落在BC边上的点H处，点D的对应点为点M，CD与HM交于点P．当点H落在BC的中点时，且，则m＝　　．

【答案】．
【解答】解：∵＝，
设CP＝t，则CD＝AB＝3t，
∵点H是BC的中点，
∴CH＝BH＝BC，
∵△CHP∽△BEH，
∴＝，
即＝，
∴BC2＝4BE•t①，
∵AE＝AB﹣BE，AE＝EH，CD＝AB＝3t，
∴AE＝EH＝3t﹣BE，
在Rt△BEH中，EH2＝BE2+BH2，
∴（3t﹣BE）2＝BE2+（BC）2②，
解①②得BE＝t，
∴BC2＝4BE•t＝4×t＝t2，
∴BC＝t，
∴m＝＝＝．
故答案为：．