第1章 特殊平行四边形素养集训1 菱形性质与判定的灵活运用 作业课件

这是一份第1章 特殊平行四边形素养集训1 菱形性质与判定的灵活运用 作业课件，共14页。

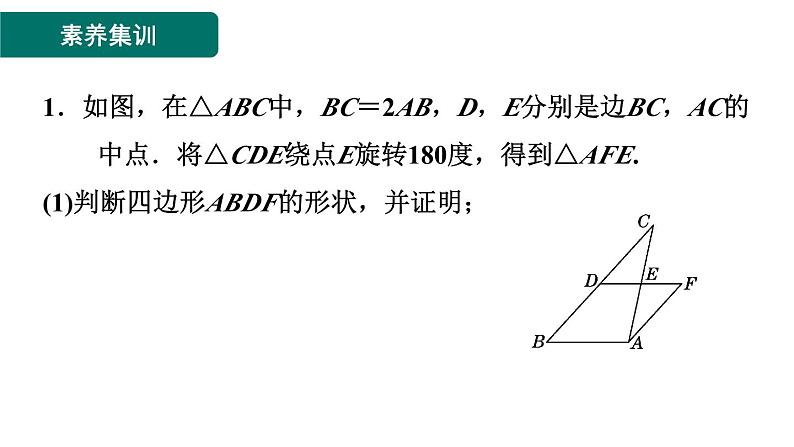
素养集训 第一章　特殊平行四边形1．菱形性质与判定的灵活运用1．如图，在△ABC中，BC＝2AB，D，E分别是边BC，AC的中点．将△CDE绕点E旋转180度，得到△AFE.(1)判断四边形ABDF的形状，并证明；解：四边形ABDF是菱形．证明：由题可知D，E，F在同一条直线上．∵D，E分别是边BC，AC的中点，∴DE是△CBA的中位线．∴DE∥AB，AB＝2DE.由旋转的性质可知，DE＝EF，∴AB＝DF.又∵AB∥DF，∴四边形ABDF是平行四边形．∵BC＝2AB，BD＝DC，∴AB＝BD.∴平行四边形ABDF是菱形．(2)连接AD，BF，若AB＝3，AD＋BF＝8，求四边形ABDF的面积S.2．如图，在四边形ABCD中，AD∥BC，对角线BD的垂直平分线与边AD，BC分别相交于点M，N.(1)求证：四边形BNDM是菱形；证明：∵AD∥BC，∴∠DMO＝∠BNO.∵MN是对角线BD的垂直平分线，∴OB＝OD，MN⊥BD.∴△MOD≌△NOB(AAS)．∴OM＝ON.∵OB＝OD，∴四边形BNDM是平行四边形．∵MN⊥BD，∴四边形BNDM是菱形．(2)若BD＝24，MN＝10，求菱形BNDM的周长．3．【教材P7习题T3变式】如图①，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F.(1)求证：△BDF是等腰三角形．证明：由折叠得△BDC≌△BDE，∴∠DBC＝∠DBE.又∵四边形ABCD是矩形，∴AD∥BC.∴∠DBC＝∠FDB.∴∠DBE＝∠FDB.∴DF＝BF.∴△BDF是等腰三角形．(2)如图②，过点D作DG∥BE，交BC于点G，连接FG交BD于点O.①判断四边形BFDG的形状，并说明理由；解：四边形BFDG是菱形．理由：∵四边形ABCD是矩形，∴FD∥BG.又∵DG∥BE，∴四边形BFDG是平行四边形．又∵DF＝BF，∴平行四边形BFDG是菱形．②若AB＝6，AD＝8，求FG的长．4．如图，分别以Rt△ABC的斜边AB、直角边AC为边向△ABC外作等边三角形ABD和等边三角形ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠BAC＝30°.给出如下结论：①EF⊥AC；②四边形ADFE为菱形；③ AD＝4AG；④ FH＝BD.其中正确的是(　　)A．①②③B．①②④C．①③④D．②③④【答案】C【点方法】根据已知先判断△ABC≌△EFA，则∠AEF＝∠BAC，得出EF⊥AC，由等边三角形的性质得出∠BDF＝30°，从而证得△DBF≌△EFA，则AE＝DF，再由FE＝AB，得出四边形ADFE为平行四边形而不是菱形，根据平行四边形的性质得出AD＝4AG，从而得出答案．