数学选择性必修 第一册3.2 双曲线优秀第1课时课后测评

3．2.2　双曲线的简单几何性质

第1课时　 双曲线的简单几何性质

学习目标　1.掌握双曲线的简单几何性质.2.理解双曲线离心率的定义、取值范围和渐近线方程.

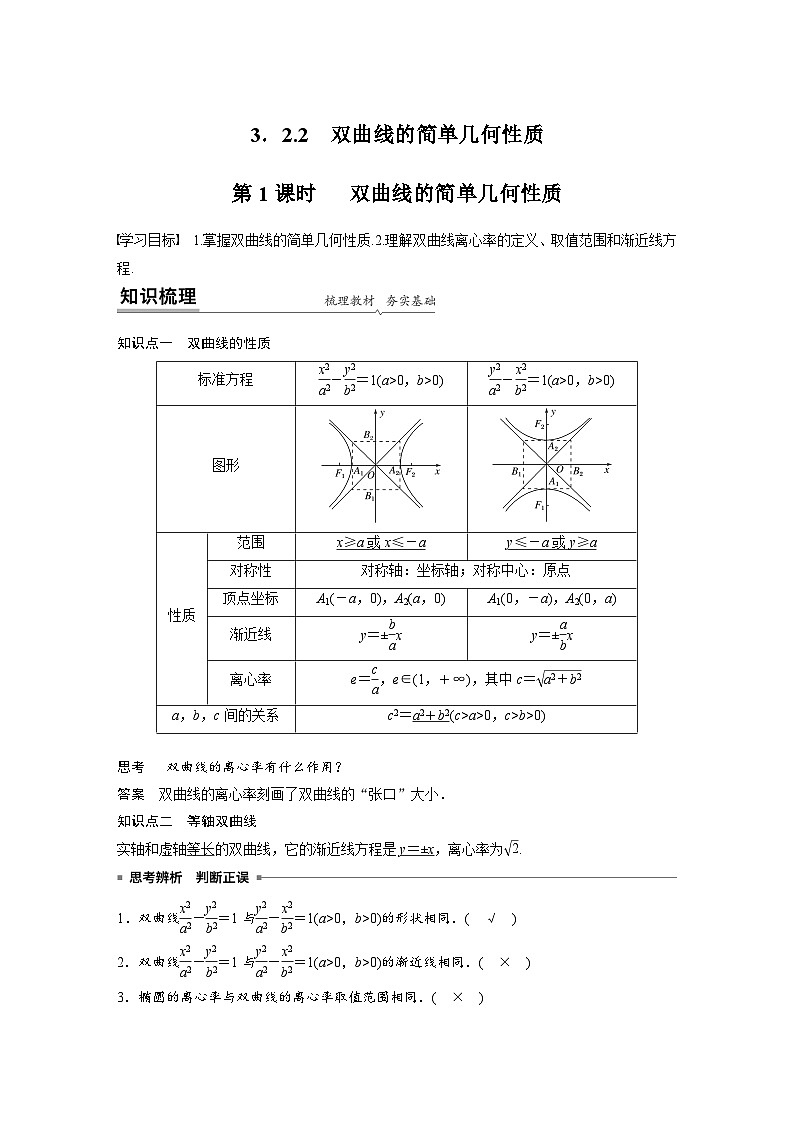
知识点一　双曲线的性质

思考　 双曲线的离心率有什么作用？

答案　双曲线的离心率刻画了双曲线的“张口”大小．

知识点二　等轴双曲线

实轴和虚轴等长的双曲线，它的渐近线方程是y＝±x，离心率为.

1．双曲线－＝1与－＝1(a>0，b>0)的形状相同．(　√　)

2．双曲线－＝1与－＝1(a>0，b>0)的渐近线相同．(　×　)

3．椭圆的离心率与双曲线的离心率取值范围相同．(　×　)

4．双曲线有四个顶点，分别是双曲线与其实轴及虚轴的交点．(　×　)

一、由双曲线方程研究其几何性质

例1　求双曲线9y2－4x2＝－36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、渐近线方程．

解　将9y2－4x2＝－36化为标准方程为－＝1，

即－＝1，

所以a＝3，b＝2，c＝.

因此顶点坐标为A1(－3,0)，A2(3,0)，

焦点坐标为F1(－，0)，F2(，0)，

实轴长2a＝6，虚轴长2b＝4，

离心率e＝＝，

渐近线方程为y＝±x＝±x.

延伸探究

求双曲线nx2－my2＝mn(m>0，n>0)的实半轴长、虚半轴长、焦点坐标、离心率、顶点坐标和渐近线方程．

解　把方程nx2－my2＝mn(m>0，n>0)化为标准方程为－＝1(m>0，n>0)，

由此可知，实半轴长a＝，

虚半轴长b＝，c＝，

焦点坐标为(，0)，(－，0)，

离心率e＝＝＝，

顶点坐标为(－，0)，(，0)，

所以渐近线方程为y＝± x，即y＝±x.

反思感悟　由双曲线的方程研究几何性质

(1)把双曲线方程化为标准形式是解决此类题的关键．

(2)由标准方程确定焦点位置，确定a，b的值．

(3)由c2＝a2＋b2求出c的值，从而写出双曲线的几何性质．

跟踪训练1　求双曲线9y2－16x2＝144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程．

解　把方程9y2－16x2＝144化为标准方程为－＝1.

由此可知，实半轴长a＝4，虚半轴长b＝3；

c＝＝＝5，焦点坐标是(0，－5)，(0,5)；

离心率e＝＝；渐近线方程为y＝±x.

二、由双曲线的几何性质求标准方程

例2　求满足下列条件的双曲线的方程：

(1)已知双曲线的焦点在x轴上，离心率为，且经过点M(－3,2)；

(2)渐近线方程为y＝±x，且经过点A(2，－3)．

解　(1)设所求双曲线方程为－＝1(a>0，b>0)．

∵e＝，∴e2＝＝＝1＋＝，

∴＝.

由题意得解得

∴所求的双曲线方程为－＝1.

(2)方法一　∵双曲线的渐近线方程为y＝±x.

当焦点在x轴上时，设所求双曲线的标准方程为－＝1(a>0，b>0)，

则＝.①

∵点A(2，－3)在双曲线上，∴－＝1.②

①②联立，无解．

当焦点在y轴上时，设所求方程为－＝1(a>0，b>0)，

则＝.③

∵点A(2，－3)在双曲线上，∴－＝1.④

联立③④，解得a2＝8，b2＝32.

∴所求双曲线的标准方程为－＝1.

方法二　由双曲线的渐近线方程为y＝±x，可设双曲线方程为－y2＝λ(λ≠0)，

∵A(2，－3)在双曲线上，∴－(－3)2＝λ，即λ＝－8.

∴所求双曲线的标准方程为－＝1.

反思感悟　由双曲线的性质求双曲线的标准方程

(1)根据双曲线的某些几何性质求双曲线方程，一般用待定系数法转化为解方程(组)，但要注意焦点的位置，从而正确选择方程的形式．

(2)巧设双曲线方程的技巧

渐近线为ax±by＝0的双曲线方程可设为a2x2－b2y2＝λ(λ≠0)．

跟踪训练2　求适合下列条件的双曲线的标准方程：

(1)焦点在x轴上，虚轴长为8，离心率为；

(2)过点(2,0)，与双曲线－＝1离心率相等．

解　(1)设所求双曲线的标准方程为－＝1(a>0，b>0)，

由题意知2b＝8，e＝＝，

从而b＝4，c＝a，

代入c2＝a2＋b2，得a2＝9，

故双曲线的标准方程为－＝1.

(2)当所求双曲线的焦点在x轴上时，

可设其方程为－＝λ(λ>0)，

将点(2,0)的坐标代入方程得λ＝，

故所求双曲线的标准方程为－y2＝1；

当所求双曲线的焦点在y轴上时，

可设其方程为－＝λ(λ>0)，

将点(2,0)的坐标代入方程得λ＝－<0(舍去)．

综上可知，所求双曲线的标准方程为－y2＝1.

三、求双曲线的离心率

例3　已知圆C：x2＋y2－10y＋21＝0与双曲线－＝1(a>0，b>0)的渐近线相切，则该双曲线的离心率是(　　)

A.  B.  C.  D.

答案　C

 解析　由双曲线－＝1(a>0，b>0)，可得其一条渐近线的方程为y＝x，即bx－ay＝0，

又由圆C：x2＋y2－10y＋21＝0，可得圆心为C(0,5)，半径r＝2，

则圆心到直线的距离为d＝＝，则＝2，可得e＝＝.

反思感悟　求双曲线离心率的方法

(1)直接法：若可求得a，c，则直接利用e＝得解．

(2)解方程法：若得到的是关于a，c的齐次方程pc2＋q·ac＋r·a2＝0(p，q，r为常数，且p≠0)，则转化为关于e的方程pe2＋q·e＋r＝0求解．

跟踪训练3　已知F1，F2是双曲线－＝1(a>0，b>0)的两个焦点，PQ是经过F1且垂直于x轴的双曲线的弦，如果∠PF2Q＝90°，求双曲线的离心率．

解　设F1(c，0)，将x＝c代入双曲线的方程得－＝1，那么y＝±.

由|PF2|＝|QF2|，∠PF2Q＝90°，

知|PF1|＝|F1F2|，

所以＝2c，所以b2＝2ac，

所以c2－2ac－a2＝0，

所以2－2×－1＝0，

即e2－2e－1＝0，

所以e＝1＋或e＝1－(舍去)，

所以双曲线的离心率为1＋.

1．(多选)已知双曲线方程为x2－8y2＝32，则(　　)

A．实轴长为8   B．虚轴长为4

C．焦距为6   D．离心率为

答案　ABD

解析　双曲线方程x2－8y2＝32化为标准方程为－＝1，可得a＝4，b＝2，c＝6，

所以双曲线的实轴长为8，虚轴长为4，焦距为12，离心率为.

2．双曲线mx2＋y2＝1的虚轴长是实轴长的2倍，则m的值为(　　)

A．4   B．－4

C．－   D.

答案　C

解析　由双曲线方程mx2＋y2＝1，知m<0，

则双曲线方程可化为y2－＝1，

则a2＝1，a＝1，

又虚轴长是实轴长的2倍，

∴b＝2，∴－＝b2＝4，

∴m＝－，故选C.

3．中心在原点，焦点在x轴上，且一个焦点在直线3x－4y＋12＝0上的等轴双曲线的方程是(　　)

A．x2－y2＝8   B．x2－y2＝4

C．y2－x2＝8   D．y2－x2＝4

答案　A

解析　令y＝0，得x＝－4，

∴等轴双曲线的一个焦点为(－4,0)，

∴c＝4，a2＝b2＝c2＝×16＝8，故选A.

4．中心在坐标原点，离心率为的双曲线的焦点在y轴上，则它的渐近线方程为________．

答案　y＝±x

解析　∵＝，

∴＝＝，

∴＝，∴＝，

∴＝.

又∵双曲线的焦点在y轴上，设双曲线方程－＝1(a>0，b>0)，

∴双曲线的渐近线方程为y＝±x，

∴所求双曲线的渐近线方程为y＝±x.

5．已知点(2,3)在双曲线C：－＝1(a>0，b>0)上，C的焦距为4，则它的离心率为________．

答案　2

解析　由题意知－＝1，c2＝a2＋b2＝4，解得a＝1，

所以e＝＝2.

1．知识清单：

(1)双曲线的几何性质．

(2)等轴双曲线．

(3)双曲线的离心率．

2．方法归纳：待定系数法、直接法、解方程法．

3．常见误区：

求双曲线方程时位置关系考虑不全面致错．

1．双曲线2x2－y2＝8的实轴长是(　　)

A．2  B．2  C．4  D．4

答案　C

解析　双曲线方程可变形为－＝1，所以a2＝4，a＝2，从而2a＝4，故选C.

2．已知双曲线－＝1(a>0)的右焦点为(3,0)，则双曲线的离心率等于(　　)

A.   B.

C.   D.

答案　C

解析　由题意知a2＋5＝9，解得a＝2，e＝＝.

3．已知双曲线的实轴和虚轴等长，且过点(5,3)，则双曲线方程为(　　)

A.－＝1   B.－＝1

C.－＝1   D.－＝1

答案　D

解析　由题意知，所求双曲线是等轴双曲线，设其方程为x2－y2＝λ(λ≠0)，将点(5,3)代入方程，可得λ＝52－32＝16，所以双曲线方程为x2－y2＝16，即－＝1.

4．双曲线x2－y2＝1的顶点到其渐近线的距离等于(　　)

A.  B.  C．1  D.

答案　B

解析　双曲线x2－y2＝1的渐近线方程为x±y＝0，顶点坐标为(1,0)，(－1,0)，

故顶点到渐近线的距离为.

5．已知双曲线C：－＝1(a>0，b>0)的离心率为，则双曲线C的渐近线方程为(　　)

A．y＝±x   B．y＝±x

C．y＝±x   D．y＝±x

答案　C

解析　已知双曲线C：－＝1(a>0，b>0)的离心率为，故有＝，所以＝，

解得＝.

故双曲线C的渐近线方程为y＝±x，故选C.

6．如图，双曲线C：－＝1的左焦点为F1，双曲线上的点P1与P2关于y轴对称，则|P2F1|－|P1F1|的值是________．

答案　6

解析　设F2为右焦点，连接P2F2(图略)，

由双曲线的对称性，知|P1F1|＝|P2F2|，

所以|P2F1|－|P1F1|＝|P2F1|－|P2F2|＝2×3＝6.

7．双曲线－＝1(a>0，b>0)的渐近线为正方形OABC的边OA，OC所在的直线，点B为该双曲线的焦点，若正方形OABC的边长为2，则a＝________.

答案　2

解析　设B为双曲线的右焦点，如图所示．

∵四边形OABC为正方形且边长为2，

∴c＝|OB|＝2.

又∠AOB＝，

∴＝tan ＝1，即a＝b.

又∵a2＋b2＝c2＝8，∴a＝2.

8．若一双曲线与椭圆4x2＋y2＝64有公共的焦点，且它们的离心率互为倒数，则该双曲线的方程为________．

答案　y2－3x2＝36

解析　椭圆4x2＋y2＝64可变形为＋＝1，

a2＝64，c2＝64－16＝48，

∴焦点为(0,4)，(0，－4)，离心率e＝，

则双曲线的焦点在y轴上，c′＝4，e′＝，

从而a′＝6，b′2＝12，

故所求双曲线的方程为y2－3x2＝36.

9．求适合下列条件的双曲线的标准方程．

(1)两顶点间的距离是6，两焦点所连线段被两顶点和中心四等分；

(2)渐近线方程为2x±3y＝0，且两顶点间的距离是6.

解　(1)由两顶点间的距离是6，得2a＝6，即a＝3.

由两焦点所连线段被两顶点和中心四等分可得2c＝4a＝12，即c＝6，

于是有b2＝c2－a2＝62－32＝27.

由于焦点所在的坐标轴不确定，故所求双曲线的标准方程为－＝1或－＝1.

(2)设双曲线方程为4x2－9y2＝λ(λ≠0)，

即－＝1(λ≠0)，由题意得a＝3.

当λ>0时，＝9，λ＝36，

双曲线方程为－＝1；

当λ<0时，＝9，λ＝－81，

双曲线方程为－＝1.

故所求双曲线的标准方程为

－＝1或－＝1.

10．设双曲线－＝1(0<a<b)的半焦距为c，直线l过(a，0)，(0，b)两点，已知原点到直线l的距离为c，求双曲线的离心率．

解　直线l的方程为＋＝1，即bx＋ay－ab＝0.

于是有＝c，

所以ab＝c2，两边平方，得a2b2＝c4.

又b2＝c2－a2，所以16a2(c2－a2)＝3c4，

两边同时除以a4，得3e4－16e2＋16＝0，

解得e2＝4或e2＝.

又b>a，所以e2＝＝1＋>2，则e＝2.

于是双曲线的离心率为2.

11．已知双曲线C：－＝1的焦距为10，点P(2,1)在C的渐近线上，则双曲线C的方程为(　　)

A.－＝1   B.－＝1

C.－＝1   D.－＝1

答案　A

解析　双曲线C的渐近线方程为－＝0，点P(2,1)在渐近线上，∴－＝0，即a2＝4b2，

又a2＋b2＝c2＝25，解得b2＝5，a2＝20，故选A.

12．若双曲线与椭圆＋＝1有相同的焦点，它的一条渐近线方程为y＝－x，则双曲线的方程为(　　)

A．y2－x2＝96   B．y2－x2＝160

C．y2－x2＝80   D．y2－x2＝24

答案　D

解析　设双曲线方程为x2－y2＝λ(λ≠0)，因为双曲线与椭圆有相同的焦点，且焦点为(0，±4)，所以λ<0，且－2λ＝(4)2，得λ＝－24.故选D.

13．已知A，B为双曲线E的左，右顶点，点M在E上，△ABM为等腰三角形，且顶角为120°，则E的离心率为(　　)

A.  B．2  C.  D.

答案　D

解析　不妨取点M在第一象限，如图所示，

设双曲线方程为－＝1(a>0，b>0)，则|BM|＝|AB|＝2a，∠MBx＝180°－120°＝60°，

∴M点的坐标为(2a，a)．

∵M点在双曲线上，∴－＝1，a＝b，

∴c＝a，e＝＝.故选D.

14．如果双曲线－＝1右支上总存在到双曲线的中心与右焦点距离相等的两个相异点，则双曲线离心率的取值范围是________．

答案　(2，＋∞)

解析　如图，因为|AO|＝|AF|，F(c，0)，

所以xA＝，因为A在右支上且不在顶点处，所以>a，所以e＝>2.

15．若点O和点F(－2,0)分别为双曲线－y2＝1(a>0)的中心和左焦点，点P为双曲线右支上的任意一点，则·的取值范围为(　　)

A．[3－2，＋∞)   B．[3＋2，＋∞)

C.   D.

答案　B

解析　因为F(－2,0)是已知双曲线的左焦点，所以a2＋1＝4，即a2＝3，

所以双曲线方程为－y2＝1.

设点P(x0，y0)(x0≥)，则－y＝1(x0≥)，可得y＝－1(x0≥)，

易知＝(x0＋2，y0)，＝(x0，y0)，

所以·＝x0(x0＋2)＋y＝x0(x0＋2)＋－1＝＋2x0－1，

此二次函数对应的图象的对称轴方程为x0＝－.

因为x0≥，所以当x0＝时，·取得最小值×3＋2－1＝3＋2，

故·的取值范围是[3＋2，＋∞)．

16．已知双曲线E：－＝1.

(1)若m＝4，求双曲线E的焦点坐标、顶点坐标和渐近线方程；

(2)若双曲线E的离心率为e∈，求实数m的取值范围．

解　(1)m＝4时，双曲线方程化为－＝1，所以a＝2，b＝，c＝3，

所以焦点坐标为(－3,0)，(3,0)，顶点坐标为(－2,0)，(2,0)，渐近线方程为y＝±x.

(2)因为e2＝＝＝1＋，e∈，所以<1＋<2，解得5<m<10，

所以实数m的取值范围是(5,10)．