


还剩14页未读,
继续阅读
成套系列资料,整套一键下载
2023八年级数学上册第十三章轴对称13.3等腰三角形第1课时上课课件新版新人教版
展开
这是一份2023八年级数学上册第十三章轴对称13.3等腰三角形第1课时上课课件新版新人教版,共22页。
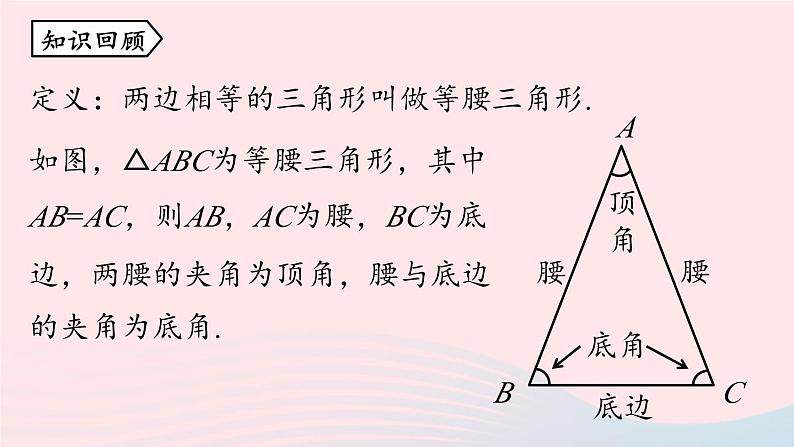
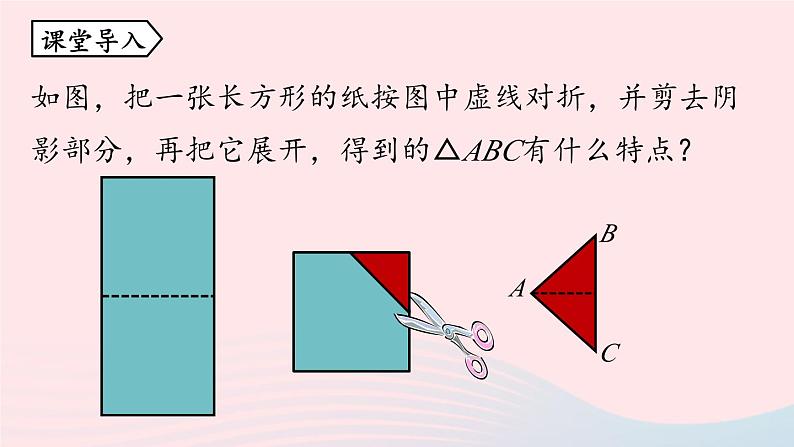
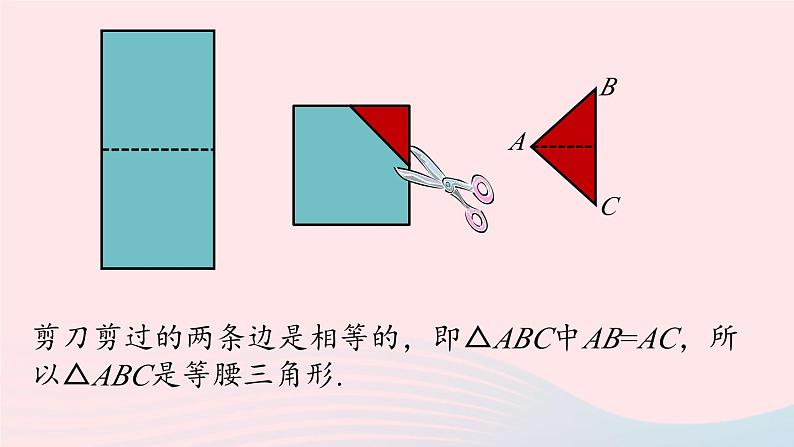
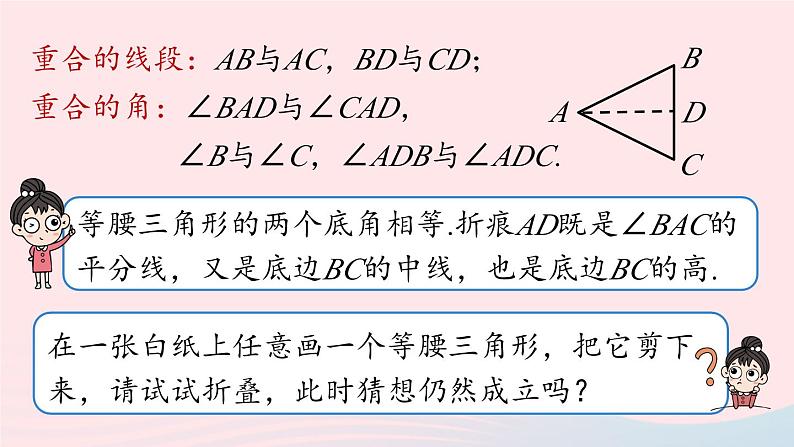
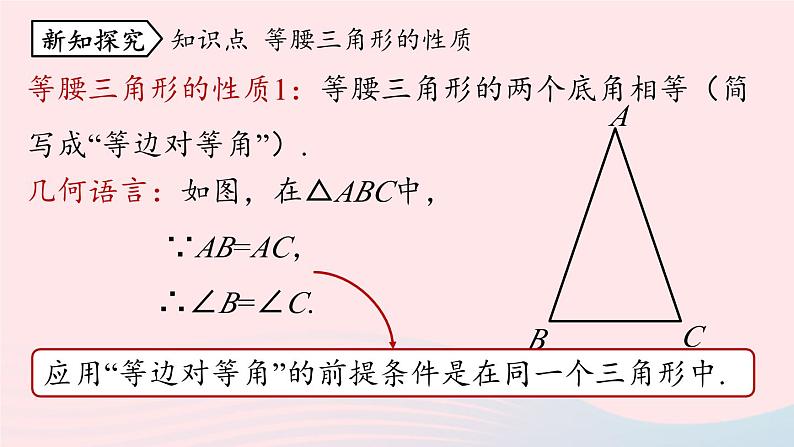
第1课时13.3.1等腰三角形八年级上册 RJ初中数学定义:两边相等的三角形叫做等腰三角形.知识回顾1.了解等腰三角形的性质,体会等腰三角形“三线合一”的意义.2.探索并掌握等腰三角形的性质,并用以解决实际问题.学习目标如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?课堂导入剪刀剪过的两条边是相等的,即△ABC中AB=AC,所以△ABC是等腰三角形.剪出的等腰三角形是轴对称图形吗?把剪出的等腰三角形ABC沿着折痕对折,找出其中重合的线段和角.重合的线段:AB与AC,BD与CD;重合的角:∠BAD与∠CAD, ∠B与∠C, ∠ADB与∠ADC.新知探究重合的线段:AB与AC,BD与CD;重合的角:∠BAD与∠CAD, ∠B与∠C,∠ADB与∠ADC.等腰三角形的性质1:等腰三角形的两个底角相等(简写成“等边对等角”).几何语言:如图,在△ABC中, ∵AB=AC, ∴∠B=∠C.知识点 等腰三角形的性质新知探究证明:作底边BC的中线AD. 在△ABD和△ACD中, AB=AC, BD=CD, AD=AD, ∴△ABD ≌△ACD(SSS). ∴∠B=∠C.ABCD已知:△ABC 中,AB=AC.求证:∠B=∠C.等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”).几何语言:如图,在△ABC中,①∵AB=AC,AD平分∠BAC, ∴AD⊥BC,BD=CD.②∵AB=AC,AD⊥BC, ∴AD平分∠BAC ,BD=CD.③∵AB=AC,BD=CD, ∴AD平分∠BAC,AD⊥BC.如图,在△ABC中,AB=AC,AD平分∠BAC,求证:AD⊥BC,BD=CD .如图,在△ABC中,AB=AC,AD是底边BC的中线,求证:AD⊥BC,AD平分∠BAC.如图,在△ABC中,AB=AC,AD是底边BC的高,求证: AD平分∠BAC ,BD=CD.跟踪训练1.(2020·福建中考)如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )A.10 B.5 C.4 D.3B新知探究2.如图,在△ABC中,已知AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )A.35° B.45° C.55° D.60°解:∵AB=AC,D为BC的中点, ∴∠B=∠C,AD⊥BC. ∵∠B=90°-∠BAD=55°, ∴∠C=55°. C1.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( ) A.40° B.36° C.80° D.25°BAB=AC, DA=DC, BD=BA等边对等角三角形外角的性质随堂练习2.如图,AB//CD,AD=CD,∠1=65°,则∠2的度数为( )A.50° B.60° C.65° D.70°三角形内角和AAB//CD,∠1=65°AD=CD∠2=50° 3.如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.等腰三角形定义性质有两边相等的三角形等边对等角三线合一课堂小结1.(2020·青海中考)等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )A.55°,55° B.70°,40°或70°,55°C.70°,40° D.55°,55°或70°,40°D拓展提升2.(2020·牡丹江中考)已知等腰三角形一边长为4,周长为10,则另两边长分别为( )A.4,2 B.3,3C.4,2或3,3 D.以上都不对C
第1课时13.3.1等腰三角形八年级上册 RJ初中数学定义:两边相等的三角形叫做等腰三角形.知识回顾1.了解等腰三角形的性质,体会等腰三角形“三线合一”的意义.2.探索并掌握等腰三角形的性质,并用以解决实际问题.学习目标如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?课堂导入剪刀剪过的两条边是相等的,即△ABC中AB=AC,所以△ABC是等腰三角形.剪出的等腰三角形是轴对称图形吗?把剪出的等腰三角形ABC沿着折痕对折,找出其中重合的线段和角.重合的线段:AB与AC,BD与CD;重合的角:∠BAD与∠CAD, ∠B与∠C, ∠ADB与∠ADC.新知探究重合的线段:AB与AC,BD与CD;重合的角:∠BAD与∠CAD, ∠B与∠C,∠ADB与∠ADC.等腰三角形的性质1:等腰三角形的两个底角相等(简写成“等边对等角”).几何语言:如图,在△ABC中, ∵AB=AC, ∴∠B=∠C.知识点 等腰三角形的性质新知探究证明:作底边BC的中线AD. 在△ABD和△ACD中, AB=AC, BD=CD, AD=AD, ∴△ABD ≌△ACD(SSS). ∴∠B=∠C.ABCD已知:△ABC 中,AB=AC.求证:∠B=∠C.等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”).几何语言:如图,在△ABC中,①∵AB=AC,AD平分∠BAC, ∴AD⊥BC,BD=CD.②∵AB=AC,AD⊥BC, ∴AD平分∠BAC ,BD=CD.③∵AB=AC,BD=CD, ∴AD平分∠BAC,AD⊥BC.如图,在△ABC中,AB=AC,AD平分∠BAC,求证:AD⊥BC,BD=CD .如图,在△ABC中,AB=AC,AD是底边BC的中线,求证:AD⊥BC,AD平分∠BAC.如图,在△ABC中,AB=AC,AD是底边BC的高,求证: AD平分∠BAC ,BD=CD.跟踪训练1.(2020·福建中考)如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )A.10 B.5 C.4 D.3B新知探究2.如图,在△ABC中,已知AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )A.35° B.45° C.55° D.60°解:∵AB=AC,D为BC的中点, ∴∠B=∠C,AD⊥BC. ∵∠B=90°-∠BAD=55°, ∴∠C=55°. C1.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( ) A.40° B.36° C.80° D.25°BAB=AC, DA=DC, BD=BA等边对等角三角形外角的性质随堂练习2.如图,AB//CD,AD=CD,∠1=65°,则∠2的度数为( )A.50° B.60° C.65° D.70°三角形内角和AAB//CD,∠1=65°AD=CD∠2=50° 3.如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.等腰三角形定义性质有两边相等的三角形等边对等角三线合一课堂小结1.(2020·青海中考)等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )A.55°,55° B.70°,40°或70°,55°C.70°,40° D.55°,55°或70°,40°D拓展提升2.(2020·牡丹江中考)已知等腰三角形一边长为4,周长为10,则另两边长分别为( )A.4,2 B.3,3C.4,2或3,3 D.以上都不对C
相关资料
更多









