2023八年级数学下册第19章一次函数19.1函数19.1.1变量与函数第4课时上课课件新版新人教版

这是一份2023八年级数学下册第19章一次函数19.1函数19.1.1变量与函数第4课时上课课件新版新人教版，共21页。

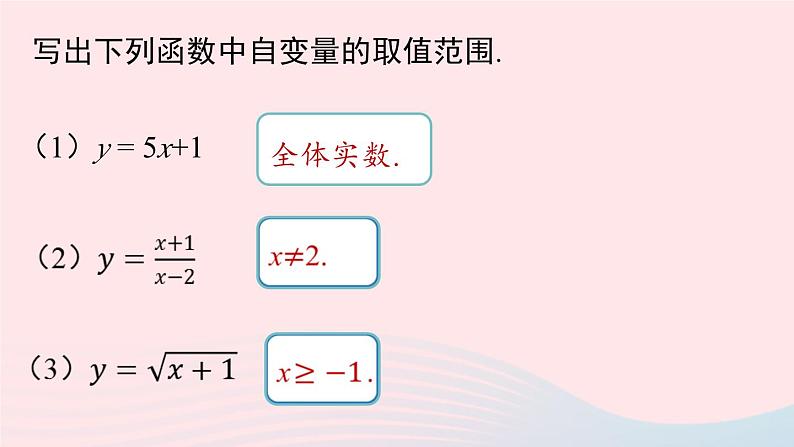
函数八年级下册 RJ初中数学19.1.1 变量与函数 课时41.函数自变量的取值范围 使函数关系式有意义的自变量取值的全体叫自变量的取值范围.1.整式型 自变量的取值范围是全体实数.2.不同类型函数自变量的取值范围2.分式型 自变量的取值范围是使分母不为0的实数.3.根式型 自变量的取值范围是使根号下的式子的值 大于或等于0的实数.4.零次型 自变量的取值范围是使幂的底数不为0的实数.知识回顾写出下列函数中自变量的取值范围.（1）y = 5x+1  全体实数.  1.了解函数解析式及函数值的概念.2.能正确的写出函数解析式并求解函数值.学习目标请写出下列问题中的函数解析式.（1）大货车以 80 km/h 的速度匀速行驶，行驶的时间为 t，行驶的路程为 s.（2）正方形的边长 x，周长为 y.解：（1）s = 80t;根据以上式子你能总结出函数解析式的定义吗？（2）y = 4x.课堂导入1.函数解析式 用关于自变量的数学式子表示函数与自变量之间的关系，是描述函数的常用方法，这种式子叫做函数的解析式.知识点：函数解析式与函数值新知探究找认真审题，根据题意找出各个量之间的数量关系.根据数量关系写出含有两个变量的等式.写变将等式变形为用含自变量的式子表示因变量的形式.确定函数解析式的步骤2.函数值 对于自变量 x 在取值范围内的某个确定的值 a，函数 y 所对应的值为 b，即当 x=a 时，y=b，则 b叫做当自变量的值为 a 时的函数值.(1)写出表示 y 与 x 的函数关系的式子；解: (1)行驶路程 x 是自变量，油箱中的油量 y 是 x 的函数，它们的关系为 y= 50-0.1x.例 汽车油箱中有汽油 50 L. 如果不再加油，那么油箱中的油量 y (单位：L)随行驶路程 x(单位：km)的增加而减少，耗油量为 0.1 L/km.(2)指出自变量 x 的取值范围；解: (2) 仅从式子 y=50-0.1x 看，x 可以取任意实数. 但考虑到 x 代表的实际意义，因此 x 不能取负数.行驶中的耗油量为 0.lx，它不能超过油箱中原有汽油量，即 0.l x ≤50，因此，自变量 x 的取值范围是 0≤ x ≤500.(3)汽车行驶 200 km 时，油箱中还有多少汽油？解: (3)汽车行驶 200 km 时，油箱中的汽油量是函数 y=50-0.lx 在 x=200 时的函数值.将 x=200 代入 y=50-0.1x，得 y=50-0.1×200=30.汽车行驶 200 km 时，油箱中还有 30 L 汽油.1.拖拉机开始工作时，油箱中有油 36 L，如果每小时耗油4 L，那么油箱中剩余油量 y L 与工作时间 x h 之间的函数解析式是 ，自变量 x 的取值范围是 ，当 x=4 时，函数值 y= .跟踪训练新知探究y = 36- 4x 0 ≤ x ≤ 920分析：x h的耗油量为4x，则剩余油量=总油量-已经消耗的油量,即y = 36- 4x .由题意知，0≤ 36- 4x ≤36.当x=4 时， y= 36-4 ×4=20.2.甲乙两地相距 150 公里，张三驾驶私家车从甲地开往乙地，并且以每小时 45 公里的速度匀速行驶，t 小时后张三距离乙地 s 公里，请写出 s 和 t 的函数解析式，并计算 3 小时后，s 的值为多少？解：每小时行驶 45 公里，t 小时行驶了45t 公里.  1.某火力发电厂共储存煤1 000吨，每天发电用煤50吨，设发电天数为 x，该发电厂开始发电后，储存煤量为 y 吨. 请写出 y 与 x 之间的函数解析式及自变量 x 的取值范围.分析：运用等量关系“储存煤量=总储存煤量-用煤量”列函数解析式. 解：由题意知，发电 x 天用煤量为 50x 吨，发电前共储存煤1 000吨.所以 y 与 x之间的函数解析式为 y=-50x+1000(0≤x≤20).随堂练习易错警示：对自变量的的取值范围考虑不周致错自变量的取值范围不仅要使所列函数解析式有意义，还要使实际问题有意义.本题中x表示天数，其值应为非负数，由题意可知1 000吨煤最多用20天，即x的最大值为20，所以x的取值范 围为0≤x≤20.2.小明带着 100 元去超市买汽水，已知一瓶汽水为 5 元，那么小明剩余的钱数 y 与购买汽水的数量 x 之间的函数解析式是什么？自变量的取值范围是多少？分析：根据“剩余的钱数 = 总钱数 - 购买汽水花费的钱数”列出函数解析式.解：一瓶汽水 5 元，则购买 x 瓶汽水花费 5x 元.函数解析式为 y = 100 - 5x.根据实际问题有意义，得自变量 x 的取值范围是 0 ≤ x ≤ 20.3.一盒中性笔有 10 支，价格为 15 元. 请写出购买中性笔支数 x 与花费的总钱数 y 之间的关系式.解：根据题意，得 10 支中性笔的价格为 15 元，则 1 支中性笔的价格为 1.5 元. 解析式函数值用关于自变量的数学式子表示函数与自变量之间的关系，是描述函数的常用方法，这种式子叫做函数的解析式.对于自变量x在取值范围内的某个确定的值a，函数y所对应的值为b，b即为函数值.函数解析式和函数值课堂小结1.李老师带着学生去科技馆参观，李老师的票价为 40 元，每个学生的票价为 30 元，试写出李老师应带门票的总费用 y（元）和学生人数 x 之间的函数解析式. 解：因为每个学生的票价为 30 元，所以 x 个学生的门票总费用是 30x.李老师应带的门票的总费用=李老师的门票费用 + 所有学生的门票总费用，即 y = 40+30x.拓展提升2.本市出租车的收费标准如下：乘坐公里数不超过 3 公里的，一律按照 10 元收费；超过 3 公里的部分，每公里加收 3 元. 设乘坐公里数为 x 公里，相对应的收费为 y 元.（1）请分别写出 x>3 和 03 时，超过 3 公里的部分，每公里加收 3元，则 y =10+3（x-3）=3x+1.2.本市出租车的收费标准如下：乘坐公里数不超过 3 公里的，一律按照 10 元收费；超过 3 公里的部分，每公里加收 3 元. 设乘坐公里数为 x 公里（x 为整数），相对应的收费为 y 元.（2）直接写出当 x=2 和 x=5 时的函数值.解：因为0< 2 < 3 ，所以当 x=3时，收费为 10 元.因为 5 >3 ，所以当 x=5 时，收费为 16 元.