第九章 不等式与不等式组【过知识课件】-2022-2023学年七年级数学下册单元复习过过过（人教版）

这是一份第九章 不等式与不等式组【过知识课件】-2022-2023学年七年级数学下册单元复习过过过（人教版），共44页。

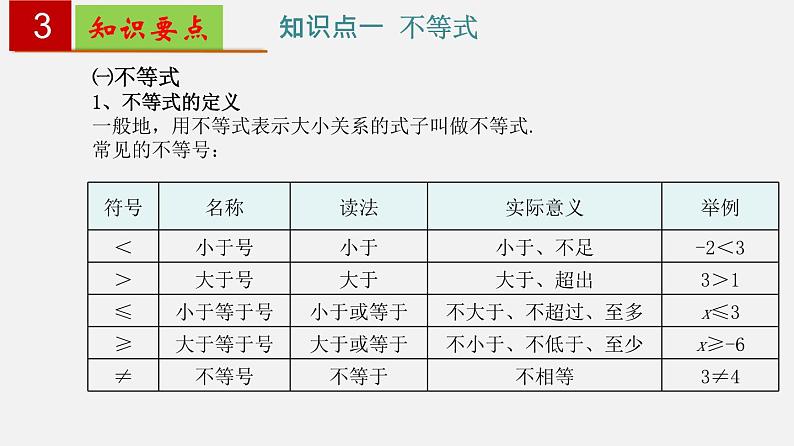
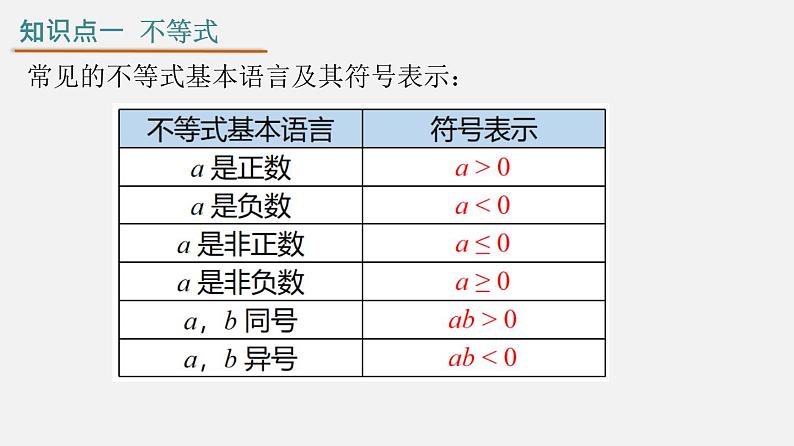
人教版七年级下册第九章 不等式与不等式组1.感受生活中存在着大量的不等关系，了解不等式和一元一次不等式的意义，通过解决简单的实际问题，使学生自发地寻找不等式的解，会把不等式的解集正确地表示到数轴上；2.经历由具体实例建立不等模型的过程，经历探究不等式解与解集的不同意义的过程，渗透数形结合思想;3.通过对不等式、不等式解与解集的探究，引导学生在独立思考的基础上积极参与对数学问题的讨论，培养他们的合作交流意识;让学生充分体会到生活中处处有数学，并能将它们应用到生活的各个领域。复习目标复习重点重难点：一元一次不等式（组）的解法和用一元一次不等式（组）解决实际问题。 复习目标 2 知识要点 3知识点一 不等式 ㈠不等式1、不等式的定义一般地，用不等式表示大小关系的式子叫做不等式.常见的不等号：知识点一 不等式 常见的不等式基本语言及其符号表示：2、不等式的解使不等式成立的未知数的值叫做不等式的解.知识点一 不等式判断一个数是不是不等式的解的方法判断一个数是否为不等式的解，就是将这个数代替不等式中的未知数，看不等式是否成立.若成立，则该数是不等式的一个解，反之不是.一般地，一个含有未知数的不等式的所有的解，组成这个不等式的解集.注意！不等式的解集必须符合两个条件：(1)解集中的每一个数值都能使不等式成立；(2)能够使不等式成立的所有数值都在该解集中.3、不等式的解集4、解不等式求不等式的解集的过程叫做解不等式.知识点一 不等式不等式的解与不等式的解集的区别与联系5、用数轴表示不等式的解集的步骤:1.定边界点：在数轴上要标出原点和边界点，注意是实心圆点还是空心圆圈，有等号边界点画实心圆点(表示包括这一点)，无等号边界点画空心圆圈(表示不包括这一点)；2.定方向：大于向右，小于向左.知识点一 不等式6、不等式的性质不等式的性质1：不等式两边加（或减）同一个数（或式子），不等号的方向不变。 即如果a＞b，那么a±c＞b±c.不等式的性质2：不等式两边乘（或除以）同一个正数，不等号的方向不变.即如果a>b，c>0，那么ac>bc (或 ).不等式的性质3：不等式两边乘（或除以）同一个负数，不等号的方向改变.即如果a>b，c<0，那么acb，则 bb，b>c，则 a>c.例1.判断下列式子是不是不等式：(1) -3＞0； (2) 4x＋3y＜0；(3) x = 3； (4) x2＋xy＋y2；(5) x＋2＞y＋5.解：(1) (2) (5) 是不等式； (3) (4) 不是不等式.【典例讲解】 D不等式两边乘(或除以)同一个负数，不等号的方向改变.【典例讲解】B【变式训练】2.利用不等式的性质解不等式3x＜2x＋1,得　 　. x＜1 知识要点 4知识点二 一元一次不等式 （二）一元一次不等式1.含有一个未知数，未知数的次数是1的不等式，叫做一元一次不等式.一元一次不等式必须同时满足三个条件：(1)不等式的两边都是整式；(2)只含有一个未知数；(3)未知数的次数是 1.知识点二 一元一次不等式2.解一元一次不等式步骤：去分母 去括号 移项 合并同类项 系数化为1.在系数化为1的这一步中,要特别注意不等式的两边都乘以(或除以)一个负数时,不等号的方向必须改变方向. 知识点二 一元一次不等式解一元一次方程与解一元一次不等式的相同点和不同点知识点二 一元一次不等式3.列一元一次不等式解决实际问题的一般步骤(1)审:弄清题意和题目中的数量关系,找出题中的不等关系,要抓住题中的关键字;(2)设:可以直接设,也可以间接设;(3)列:根据题目中能表示全部含义的不等关系列出不等式;(4)解:解出所列的不等式的解集;(5)验:检验所得结果是否正确,考虑所得的解是否符合问题的实际意义;(6)答:写出答案.知识点二 一元一次不等式知识点二 一元一次不等式(1) 2－5x ＜ 8－6x ； （2）解：合并同类项，得：x ＜ 6.移项，得 －5x＋6x ＜ 8－2，例3 解不等式，并把解集表示在数轴上.不等式的解集在数轴上表示如图所示：【典例讲解】解：去分母，得 2(2x－1)－(9x＋2)≤6，去括号，得 4x－2－9x－2≤6，移项，得 4x－9x≤6＋2＋2，合并同类项，得 －5x≤10，系数化 1，得 x≥－2.不等式的解集在数轴上表示如图所示.（2）【典例讲解】解：由 ，得例5.倡导健康生活,推进全民健身.某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套280元,430元,且每种型号健身器材必须整套购买.若购买A,B两种型号的健身器材共50套,且支出不超过16 000元,A种型号健身器材至少要购买多少套?【典例讲解】3（1）求不等式 3x+1≥4x-5的正整数解．移项得:合并同类项得:化系数为1得:解:3x﹣4x≥-5-1﹣x ≥-6x≤6所以不等式 的正整数解为：1、2、3、4、5、6【变式训练】 8x-4≥15x-608x-15x≥-60+4 -7x≥-56 x≤8去分母得:去括号得:移项得:合并同类项得:化系数为1得:解:同除以-7,方向改变解：解不等式 x+m＜1，得 x＜1-m.根据题意得 3＜1-m≤4，即 -3≤m＜-2.4. 若关于 x 的不等式 x+m＜1 只有 3 个正整数解，则 m 的取值范围是___________.-3≤m＜-2【变式训练】 5.某服装店计划购进一批甲、乙两种款式的运动服进行销售，进价和售价如下表所示：若购进两种款式的运动服共300套，且投入资金不超过26 800元．【变式训练】该服装店应至少购进甲款运动服多少套？ 知识要点 5知识点三 一元一次不等式组 （三）一元一次不等式组 1.一元一次不等式组的定义：类似于方程组，把几个含有相同未知数的一元一次不等式合起来，就组成一个一元一次不等式组.一元一次不等式组必须同时满足三个条件：①每个不等式都是一元一次不等式；②含有同一个未知数；③不等式的个数不少于2. 知识要点 5知识点三 一元一次不等式组 注意！“公共部分”是指同时满足不等式组中每一个不等式的解集的部分.如果组成不等式组的各个不等式的解集没有公共部分，则这个不等式组无解.2.一元一次不等式组的解集一般地，几个不等式的解集的公共部分，叫做由它们所组成的不等式组的解集.一元一次不等式组的解集有四种情况：x>ax