2024全国一轮数学（基础版）第28讲 数列的概念与简单表示课件PPT

这是一份2024全国一轮数学（基础版）第28讲 数列的概念与简单表示课件PPT，共35页。PPT课件主要包含了链教材·夯基固本，激活思维，ABC，an＝－4n＋2，基础回归，序号n，Sn－Sn－1，研题型·融会贯通，举题说法，n－5等内容，欢迎下载使用。

1. (人A选必二P5例3改)已知数列{an}的通项公式为an＝n2＋2n，那么120是这个数列的第________项(　 　)A. 9 B. 10 C. 11 D. 12
【解析】 令n2＋2n＝120，得n＝－12(舍去)或n＝10，所以120是数列{an}的项，且是第10项．
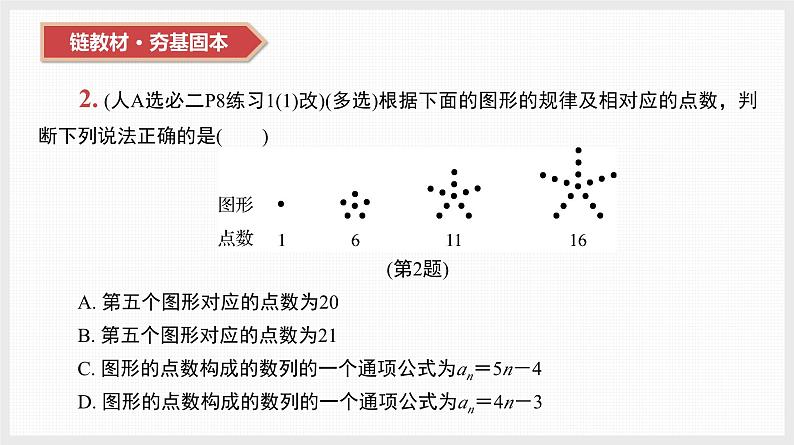
2. (人A选必二P8练习1(1)改)(多选)根据下面的图形的规律及相对应的点数，判断下列说法正确的是(　　)(第2题)A. 第五个图形对应的点数为20B. 第五个图形对应的点数为21C. 图形的点数构成的数列的一个通项公式为an＝5n－4D. 图形的点数构成的数列的一个通项公式为an＝4n－3
【解析】 设第n项的点数为an(n∈N*)，因为a1＝1，a2＝1＋5，a3＝1＋2×5，a4＝1＋3×5，所以该数列的第5项为a5＝1＋4×5＝21，数列{an}的一个通项公式为an＝1＋5(n－1)＝5n－4，且第5项的图形如图所示．(第2题)
4. (人A选必二P8练习4改)已知数列{an}的前n项和公式为Sn＝－2n2，则{an}的通项公式为____________________.
【解析】 当n≥2时，an＝Sn－Sn－1＝－2n2＋2(n－1)2＝－4n＋2；当n＝1时，a1＝S1＝－2，满足an＝－4n＋2，故{an}的通项公式为an＝－4n＋2.
1. 数列的通项公式如果数列{an}的第n项与__________之间的关系可以用一个式子来表示，那么这个公式叫做这个数列的通项公式．2. an与Sn的关系
3. 数列的递推公式如果已知数列的第1项(或前几项)，且从第二项(或某一项)开始的任一项an与它的前一项an－1(或前几项)间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的递推公式．由递推公式求通项的常用方法：
例1　写出下面数列的一个通项公式，使它的前4项分别是下列各数：
【解答】 这个数列的前4项构成一个摆动数列，奇数项是2，偶数项是0，所以它的一个通项公式为an＝(－1)n＋1＋1.
(2) 2,0,2,0，….
已知数列的前几项求通项公式，主要从以下几个方面来考虑：(1) 负号用(－1)n与(－1)n＋1或(－1)n－1来调节，这是因为n和n＋1奇偶交错．(2) 公式形式的数列，分子、分母找通项，要充分借助分子、分母的关系．(3) 对于比较复杂的通项公式，要借助于等差数列、等比数列和其他方法解决．
【解析】 数列中各项的符号可通过(－1)n表示，从第2项起，每一项的绝对值总比它的前一项的绝对值大6，故通项公式为an＝(－1)n(6n－5)．
　　　(1) －1,7，－13,19，…的一个通项公式为_____________________；
(－1)n(6n－5)
【解析】 a1＝S1＝2－3＝－1，当n≥2时，an＝Sn－Sn－1＝(2n2－3n)－[2(n－1)2－3(n－1)]＝4n－5，由于a1＝－1也符合此等式，所以an＝4n－5.
例2　(1) 已知数列{an}的前n项和Sn＝2n2－3n，则an＝____________.
【解析】 因为Sn＝2an＋1，当n≥2时，Sn－1＝2an－1＋1，所以an＝Sn－Sn－1＝2an－2an－1(n≥2)，即an＝2an－1(n≥2)．当n＝1时，a1＝S1＝2a1＋1，得a1＝－1，所以数列{an}是首项 a1＝－1，公比q＝2的等比数列，
(2) 记Sn为数列{an}的前n项和．若Sn＝2an＋1，则S6＝__________.
Sn与an的关系问题转化的两个方向：(1) 利用an＝Sn－Sn－1(n≥2)转化为只含Sn，Sn－1的关系式，再求解；(2) 利用Sn－Sn－1＝an(n≥2)转化为只含an，an－1的关系式，再求解．
　　　(1) 记Sn为数列{an}的前n项和．若Sn＝3an＋6，则Sn＝__________.
例3　(1) 在数列{an}中，已知a1＝1，(n＋1)·an＋1＝n·an，则{an}的通项公式为____________.
【解析】 因为当n≥2时，an＋1－5an＋4an－1＝0，所以an＋1－an＝4(an－an－1)，所以{an＋1－an}是以4为公比，a2－a1＝1为首项的等比数列，所以an＋1－an＝4n－1，
(2) 已知数列{an}，a1＝1，a2＝2，an＋1－5an＋4an－1＝0(n∈N*，n≥2)，则{an}的通项公式为________________.
【解析】 设an＋t＝2(an－1＋t)，则an＝2an－1＋t，与an＝2an－1＋1(n≥2)进行比较，可得t＝1，则有an＋1＝2(an－1＋1)．设bn＝an＋1，则有bn＝2bn－1，所以{bn}是以b1＝a1＋1＝－2为首项，2为公比的等比数列，所以bn＝(－2)2n－1，所以an＝bn－1＝(－2)2n－1－1＝－2n－1.
(3) 已知数列{an}中，a1＝－3且当n≥2时，an＝2an－1＋1，则{an}的通项公式为____________________.
一般地，对于形如an＋1＝an＋f(n)类的通项公式，只要f(1)＋f(2)＋…＋f(n)能进行求和，则宜采用叠加法求解；对于形如an＋1＝f(n)·an类的通项公式，当f(1)·f(2)·…·f(n)的值可以求得时，宜采用累乘法求解；对于形如an＋1＝can＋d的递推数列求通项公式，可通过适当换元，转换成等比数列或等差数列求解．
【解析】 由题知an＋1－an＝－n，则当n≥2时，a2－a1＝－1，a3－a2＝－2，a4－a3＝－3，…，an－an－1＝－(n－1)，
　　　(1) 已知数列{an}中，a1＝1，an＋1＝an－n，则{an}的通项公式为________________________.
(2) 已知数列{an}中，a1＝1，an＋1＝2n·an，则{an}的通项公式为______________.
1. 若数列{an}的前n项和Sn＝n2＋n，则a4的值为(　 　)A. 4 B. 6 C. 8　　 D. 10
点击对应数字即可跳转到对应题目
【解析】 由题知，当n≥2时，an＝Sn－Sn－1＝n2＋n－(n－1)2－(n－1)＝2n，所以a4＝8.
2. 已知数列{an}的前n项和为Sn＝n2·an(n≥2)，a1＝1，通过计算a2，a3，a4，可猜想an等于(　 　)
【解析】 因为Sn＝n2an，所以an＋1＝Sn＋1－Sn＝(n＋1)2an＋1－n2an，
3. 已知数列9,12,17,24,33，…，则此数列的一个通项公式为_______________.
【解析】 因为当n≥2时，a2－a1＝3，a3－a2＝5，a4－a3＝7，…，an－an－1＝2n－1，以上各式相加得an－a1＝3＋5＋7＋…＋(2n－1)，所以an＝n2＋8(n∈N*，n＝1时也符合此式)．
an＝n2＋8(n∈N*)
4. 已知数列{an}中，a1＝1，an＋1＝en·an，则数列{an}的通项公式为__________.