2024全国一轮数学（基础版）第32讲 空间几何体的表面积和体积课件PPT

这是一份2024全国一轮数学（基础版）第32讲 空间几何体的表面积和体积课件PPT，共44页。PPT课件主要包含了链教材·夯基固本，激活思维，基础回归，任一边，任一直角边，垂直于底边的腰，πrl，πr1＋r2l，πR2，研题型·融会贯通等内容，欢迎下载使用。
1. (人A 必二P119练习1)已知圆锥的表面积为am2，且它的侧面展开图是一个半圆，则这个圆锥的底面直径为_____________.
【解析】 设圆锥的底面半径为rm，母线长为lm，则由题意得a＝πr2＋πrl①.又圆锥的侧面展开图为半圆，所以2πr＝πl，即l＝2r②.
2. (人A 必二P119练习2)当一个球的半径为______时，其体积和表面积的数值相等．
3. (人A 必二P120习题5改)设一个正方体的顶点都在球面上，它的棱长是acm，则球的体积为(　 　)
4. (人A 必二P116练习1)若正六棱台的上、下底面边长分别是2cm和6cm，侧棱长是5cm，则它的表面积为____________________________.
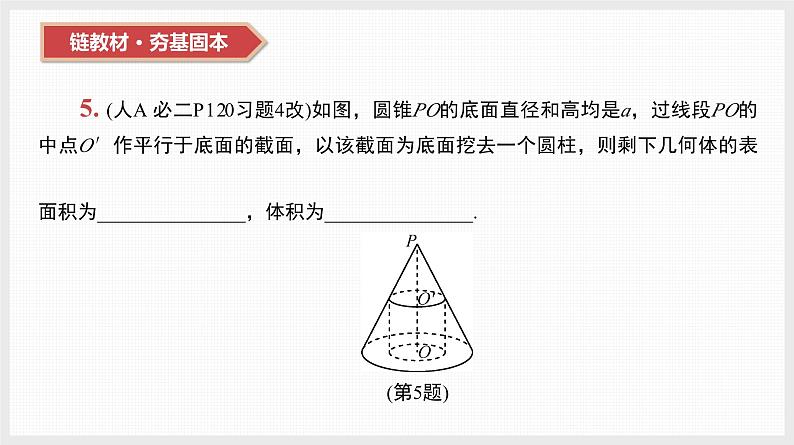
5. (人A 必二P120习题4改)如图，圆锥PO的底面直径和高均是a，过线段PO的中点O′作平行于底面的截面，以该截面为底面挖去一个圆柱，则剩下几何体的表 面积为_______________，体积为_______________.(第5题)
1. 空间几何体的结构特征(1) 多面体的结构特征
(2) 旋转体的结构特征
2. 圆柱、圆锥、圆台的侧面展开图及侧面积公式
3. 柱、锥、台、球的表面积和体积
例1　木升子是一种民间称量或盛装粮食的工具(如图所示)，呈正棱台形，一般由四块梯形木和一块正方形木组成，其上口是一个正方形，下面是一个封口较小的正方形．现有一木升子(厚度忽略不计)，其上口周长为52cm，下口周长为40cm，侧面等腰梯形腰长为8cm，则该木升子的侧面积约为(结果精确到0.1cm2，参考数据：≈15.72)(　 　)A. 90.4cm2 B. 180.8cm2C. 361.6cm2 D. 368.0cm2
空间几何体表面积的求法：(1) 多面体：其表面积是各个面的面积之和；(2) 旋转体：其表面积等于侧面面积与底面面积的和；(3) 简单组合体：应搞清各构成部分，并注意重合部分的删、补．
(1) 若所给定的几何体为可直接用公式求解的柱体、锥体或台体，则可直接利用公式进行求解；(2) 若所给定的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法进行求解．
　　　(1) (2022·湛江一模)如图所示是战国时期的一个铜镞，其由两部分组成，前段是高为2cm，底面边长为1cm的正三棱锥，后段是高为0.6cm的圆柱，圆柱底面圆与正三棱锥底面的正三角形内切，则此铜镞的体积约为(　 　)(变式(1))A. 0.25cm3 B. 0.65cm3 C. 0.15cm3 D. 0.45cm3
(2) 如图，已知三棱柱ABC －A1B1C1的所有棱长均为1，且AA1⊥底面ABC，那么三棱锥B1 －ABC1的体积为(　 　)
例3　如图，在圆锥SO中，已知底面半径r＝1，母线长l＝4，M为母线SA上的一点，且SM＝x，从点M拉一根绳子，围绕圆锥侧面转到点A. (1) 求绳子的最短长度的平方f(x)；(例3)
【解答】 当绳子最短时，在展开图中作SR⊥AM，垂足为R，则SR的长度即为顶点S到绳子的距离．
(2) 当绳子最短时，求顶点到绳子的距离；
【解答】 因为f(x)＝x2＋16(0≤x≤4)是增函数，所以f(x)的最大值为f(4)＝32.
(3) 求f(x)的最大值．
空间几何体表面上距离的最小问题的解题思路是将空间几何体的侧面展开，把立体几何问题转化为平面几何问题，然后利用平面几何知识去解决．
　　　已知正三棱柱木块ABC－A1B1C1，其中AB＝2，AA1＝3，如图，一只蚂蚁自A点出发经过线段BB1上的一点M到达点C1，当沿蚂蚁走过的最短路径截开木块时，两部分几何体的体积之比为__________.(变式)
【解析】 如图，将正三棱柱ABC－A1B1C1沿棱BB1展开成平面，AC1与BB1的交点即为满足AM＋MC1最小时的点M.　　　　　　(变式)
A. 100π B. 128π C. 144π D. 192π
【解析】 易知半径最大的球为圆锥的内切球，球与圆锥内切时的轴截面如图所示，其中BC＝2，AB＝AC＝3，且M为BC边上的中点．
(2) 若圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为___________.
多面体与球的切、接问题的求解方法：(1) 涉及球与棱柱、棱锥的切、接问题时，一般过球心及多面体的特殊点(一般为接、切点)或线作截面，把空间问题转化为平面问题求解．(2) 若球面上四点P，A，B，C构成的三条线段PA，PB，PC两两垂直，且PA＝a，PB＝b，PC＝c，一般把有关元素“补形”成为一个球内接长方体，根据4R2＝a2＋b2＋c2求解．(3) 正方体的内切球的直径为正方体的棱长．(4) 正方体的外接球的直径为正方体的体对角线长．(5) 利用平面几何知识寻找几何体中元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解．
1. 已知一个圆锥的底面半径为6，其体积为30π，则该圆锥的侧面积为_______.
点击对应数字即可跳转到对应题目
2. 如图所示是古希腊数学家阿基米德的墓碑文，墓碑上刻着一个圆柱，圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等，相传这个图形是阿基米德最引以为豪的发现，我们来重温这个伟大发现，圆柱的表面积与球的表面积之比为(　 　)