





2024全国一轮数学(基础版)第45讲 随机抽样的方法、用样本估计总体课件PPT
展开1. (人A 必二P181练习1)为了合理调配电力资源,某市欲了解全市50 000户居民的日用电量.若通过简单随机抽样从中抽取了300户进行调查,得到其日用电量的平均数为5.5 kW·h,则可以推测全市居民用户日用电量的平均数( )A. 一定为5.5 kW·h B. 高于5.5 kW·hC. 低于5.5 kW·h D. 约为5.5 kW·h
【解析】 样本平均数是对总体平均数的一种估计,它们之间没有确定的大小关系,所以A,B,C均错误.
2. (人A 必二P224复习题1改)为了调查参加运动会的1 000名运动员的年龄情况,从中抽查了100名运动员的年龄,就这个问题来说,下列说法正确的是( )A. 1 000名运动员是总体B. 每个运动员是个体C. 抽取的100名运动员是样本D. 样本容量是100
【解析】 就这个问题,我们研究的是运动员的年龄情况,故总体是1 000名运动员的年龄,个体是每个运动员的年龄,样本是100名运动员的年龄.
3. (人A 必二P185练习3改)一支田径队有男运动员56名,女运动员42名,按性别进行分层,用分层随机抽样的方法从全体运动员中抽出一个容量为28的样本.如果样本按比例分配,那么男运动员应抽取________名,女运动员应抽取________名.
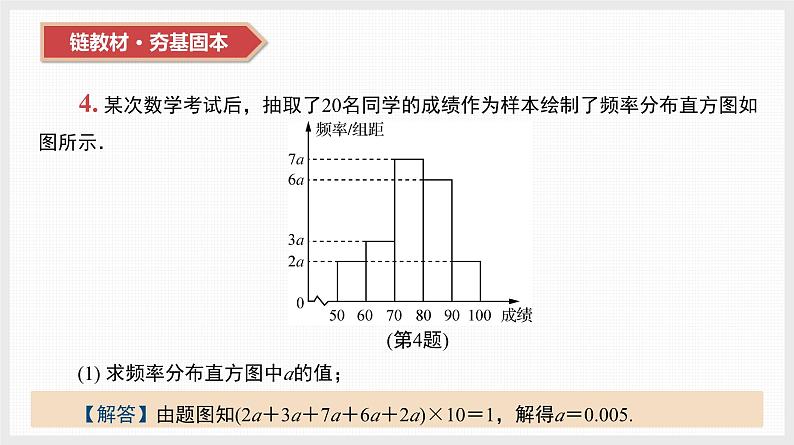
4. 某次数学考试后,抽取了20名同学的成绩作为样本绘制了频率分布直方图如图所示.(第4题)(1) 求频率分布直方图中a的值;
【解答】由题图知(2a+3a+7a+6a+2a)×10=1,解得a=0.005.
(2) 求20位同学成绩的平均分;
【解答】 20位同学成绩的平均分为(55×2a+65×3a+75×7a+85×6a+95×2a)×10=76.5.
(3) 估计样本数据的第一四分位数和第80百分位数(保留三位有效数字).
【解答】由图可知,[50,60),[60,70),[70,80),[80,90),[90,100]对应的频率分别为0.1,0.15,0.35,0.3,0.1,前两组频率之和恰为0.25,故第一四分位数为70.0.前三组频率之和为0.6,前四组频率之和为0.9,所以第80百分位数在第四组.设第80百分位数为x,则0.6+(x-80)×10×0.03=0.8,解得x≈80.7.
1. 简单随机抽样(1) 简单随机抽样分为放回简单随机抽样和不放回简单随机抽样.除非特殊声明,本章简单随机抽样指不放回简单随机抽样.(2) 简单随机抽样的常用方法实现简单随机抽样的方法很多,抽签法和随机数法是比较常用的两种方法.
2. 总体平均数与样本平均数
3. 分层随机抽样(1) 分层随机抽样的概念一般地,按一个或多个变量把总体划分成若干个子总体,每个个体属于且仅属于一个子总体,在每个子总体中独立地进行简单随机抽样,再把所有子总体中抽取的样本合在一起作为总样本,这样的抽样方法称为分层随机抽样,每一个子总体称为层.
(2) 分层随机抽样的平均数计算
4. 统计图表常见的统计图表有条形图、扇形图、折线图、频数分布直方图、频率分布直方图等(见微专题).5. 百分位数一般地,一组数据的第k百分位数是这样一个值pk,它使得这组数据中至少有_______的数据小于或等于pk,且至少有___________________的数据大于或等于pk.如果将样本数据从小到大排列成一行,那么第k百分位数pk所处位置如图所示.
6. 平均数、中位数和众数(2) 中位数:将一组数据按从小到大或从大到小的顺序排列,处在最________的一个数据(当数据个数是奇数时)或最中间两个数据的__________(当数据个数是偶数时).(3) 众数:一组数据中出现次数________的数据(即频数最大值所对应的样本数据).
8. 分层抽样数据的方差
9. 常用结论平均数、方差的公式推广(2) 若数据x1,x2,…,xn的方差为s2,则①数据x1+a,x2+a,…,xn+a的方差也为s2;②数据ax1,ax2,…,axn的方差为a2s2.
【解析】 从随机数表的第一行第3列和第4列数字开始,依次读取08,33(舍),95(舍),55(舍),02,62(舍),15,27(舍),02(舍),43(舍),69(舍),32(舍),18,18(舍),26(舍),09,则第五个编号为09.
例1 (1) 从编号依次为01,02,…,20的20人中选取5人,现从随机数表的第一行第3列和第4列数字开始,由左向右依次选取两个数字,则第五个编号为( )A. 09 B. 02 C. 15 D. 18
(2) (2022·惠州摸底)(多选)港珠澳大桥是中国境内一座连接中国香港、广东珠海和中国澳门的桥隧工程,因其超大的建筑规模、空前的施工难度以及顶尖的建造技术闻名世界,为内地前往香港的游客提供了便捷的交通途径.某旅行社分年龄统计了大桥落地以后,由港珠澳大桥实现内地前往香港的老、中、青旅客的比例分别为5∶2∶3,现使用分层随机抽样的方法从这些旅客中随机抽取n名,若青年旅客抽到60名,则( )A. 老年旅客抽到100名B. 中年旅客抽到20名C. n=200D. 被抽到的老年旅客以及中年旅客人数之和超过200
(1) 简单随机抽样需满足:①被抽取的样本总体的个体数有限;②逐个抽取;③等可能抽取.
备选 (2022·百校大联考)我校高一、高二、高三年级共有学生1 800名,为了了解同学们对某授课软件的意见,计划采用分层随机抽样的方法从这1 800名学生中抽取一个容量为72的样本.若从高一、高二、高三年级抽取的学生人数恰好是从小到大排列的连续偶数,则我校高三年级的人数为( )A. 800 B. 750 C. 700 D. 650
例2 (1) 以下数据为参加数学竞赛决赛的15人的成绩(单位:分):78,70,72,86, 88,79,80,81,94,84,56,98,83,90,91,则这15人成绩的第80百分位数是( )A. 90 B. 91.5 C. 91 D. 90.5
(2) 对某种电子元件使用寿命跟踪调查,所得样本的频率分布直方图如图所示.由图可知,这一批电子元件中寿命的85%分位数为( )(例2(2))A. 500 h B. 450 h C. 350 h D. 550 h
计算一组n个数据第p百分位数的步骤:第一步,按从小到大排列原始数据.第二步,计算i=n×p%.第三步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
例3 (多选)某城市在创建文明城市的活动中,为了解居民对“创建文明城市”的满意程度,组织居民给活动打分(分数为整数,满分100分),从中随机抽取一个容量为100的样本,发现数据均在[40,100]内.现将这些分数分成6组并画出样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,则下列说法正确的是( )A. 频率分布直方图中第三组的频数为10B. 根据频率分布直方图估计样本的众数为75分C. 根据频率分布直方图估计样本的中位数为75分D. 根据频率分布直方图估计样本的平均数为75分
【解析】 分数在[60,70)内的频率为1-10×(0.005+0.020+0.030+0.025+0.010)=0.10,所以第三组的频数为100×0.10=10,故A正确;因为众数的估计值是频率分布直方图中最高矩形底边的中点的横坐标,从图中可看出众数的估计值为75分,故B正确;因为(0.005+0.020+0.010)×10=0.35<0.5,(0.005+0.020+0.010+0.030)×10=0.65>0.5,所以中位数位于[70,80)内,设中位数为x,则0.35+0.03(x-70)=0.5,解得x=75,所以中位数的估计值为75分,故C正确;样本平均数的估计值为45×(10×0.005)+55×(10×0.020)+65×(10×0.010)+75×(10×0.030)+85×(10×0.025)+95×(10×0.010)=73(分),故D错误.
频率分布直方图的数字特征:(1) 众数:最高矩形的底边中点的横坐标.(2) 中位数:中位数左边和右边的矩形的面积和相等.(3) 平均数:平均数在频率分布直方图中等于各组区间的中点值与对应频率之积的和.
备选 (2021·全国甲卷改)(多选)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如图所示的频率分布直方图,根据此频率分布直方图,下面结论中正确的是( )A. 该地农户家庭年收入低于4.5万元的农户比率估计为6%B. 该地农户家庭年收入不低于10.5万元的农户比率估计为10%C. 估计该地农户家庭年收入的平均值不超过6.5万元D. 估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
【解析】 对于A,由频率分布直方图可知,该地农户家庭年收入低于4.5万元的农户比率估计为(0.02+0.04)×1×100%=6%,故A正确;对于B,由频率分布直方图可知,该地农户家庭年收入不低于10.5万元的农户比率估计为(0.04+0.02+0.02+0.02)×1×100%=10%,故B正确;对于C,由频率分布直方图可知,该地农户家庭年收入的平均值估计为3×0.02+4×0.04+5×0.10+6×0.14+7×0.20+8×0.20+9×0.10+10×0.10+11×0.04+12×0.02+13×0.02+14×0.02=7.68(万元),故C错误;对于D,由频率分布直方图可知,该地农户家庭年收入介于4.5万元至8.5万元之间的农户比率估计为(0.10+0.14+0.20+0.20)×1×100%=64%>50%,故D正确.
例4 甲、乙两人在相同条件下各射击10次,每次中靶环数情况如图所示.(1) 请填写下表(写出计算过程).
【解答】 甲射击10次中靶环数分别为9,5,7,8,7,6,8,6,7,7,将它们由小到大排列为5,6,6,7,7,7,7,8,8,9.乙射击10次中靶环数分别为2,4,6,8,7,7,8,9,9,10,将它们由小到大排列为2,4,6,7,7,8,8,9,9,10.
(2) 从下列三个不同的角度对这次测试结果进行分析:①从平均数和方差相结合看(分析谁的成绩更稳定);②从平均数和命中9环及9环以上的次数相结合看(分析谁的成绩好些);③从折线图上两人射击命中环数的走势看(分析谁更有潜力).
②因为两人成绩的平均数相同,但命中9环及9环以上的次数甲比乙少,所以乙成绩比甲好些.③因为甲成绩在平均数上下波动,而乙处于上升势头,从第三次以后就没有比甲少的情况发生,所以乙更有潜力.
总体离散程度的估计:标准差(方差)反映了数据的离散与集中、波动与稳定的程度.标准差(方差)越大,数据的离散程度越大;标准差(方差)越小,数据的离散程度越小.
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:(1) 根据上表作出这些数据的频率分布直方图;
【解答】 产品质量指标的频率分布直方图如图.
【解答】 质量指标值的样本平均数为80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.质量指标值的样本方差为s2=(80-100)2×0.06+(90-100)2×0.26+(100-100)2×0.38+(110-100)2×0.22+(120-100)2×0.08=104,所以这种产品质量指标值的平均数的估计值为100,方差的估计值为104.
(3) 根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少占全部产品的80%”的规定?
【解答】 质量指标值不低于95的产品所占比例的估计值为0.38+0.22+0.08=0.68.由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少占全部产品的80%”的规定.
(2) 某电池厂有A,B两条生产线制造同一型号可充电电池.现采用样本量比例分配的分层随机抽样,从某天两条生产线上的成品中随机抽取样本,并测量产品可充电次数的均值及方差,结果如下表:则20个产品组成的总样本的均值为__________,方差为________.
1. 给定一组数据5,5,4,3,3,3,2,2,2,1,则这组数据的( )A. 众数为2 B. 平均数为2.5C. 方差为1.6 D. 标准差为4
点击对应数字即可跳转到对应题目
【解析】 由题中数据可得,众数为2和3,故A错误;
2. 某机构调查了10种食品的卡路里含量,结果如下:107,135,138,140,146,175, 179,182,191,195,则这组数据的第25百分位数和中位数分别是( )A. 138,160.5 B. 138,146C. 138,175 D. 135,160.5
3. (2022·深圳模拟)(多选)若甲组样本数据x1,x2,…,xn(数据各不相同)的平均数为2,方差为4,乙组样本数据3x1+a,3x2+a,…,3xn+a的平均数为4,则下列说法正确的是( )A. a的值为-2B. 乙组样本数据的方差为36C. 两组样本数据的中位数一定相同D. 两组样本数据的极差不同
【解析】 由题意可知,3×2+a=4,则a=-2,故A正确;乙组样本数据的方差为9×4=36,故B正确;设甲组样本数据的中位数为xi,则乙组样本数据的中位数为3xi-2,所以两组样本数据的中位数不一定相同,故C错误;甲组样本数据的极差为xmax-xmin,乙组样本数据的极差为(3xmax-2)-(3xmin-2)=3(xmax-xmin),所以两组样本数据的极差不同,故D正确.
4. 将高三某班60名学生参加某次数学模拟考试所得的成绩(成绩均为整数)整理后画出频率分布直方图如图所示,则此班的本次数学模拟考试成绩的80%分位数是________________. (结果保留两位小数)
【解析】 由频率分布直方图可知,分数在120分以下的学生所占的比例为(0.01+0.015+0.015+0.03)×10×100%=70%,分数在130分以下的学生所占的比例为(0.01+0.015+0.015+0.03+0.022 5)×10×100%=92.5%,因此,80%分位数一定位于[120,130)内.
5. 某班同学的体重状况调查中,已知30名男生的平均体重为60 kg,方差为50,20名女生的平均体重为50 kg,方差为60,那么该班50名同学的平均体重为________ kg,方差为________.
2024年新高考数学第一轮复习课件:第45讲 随机抽样的方法、用样本估计总体: 这是一份2024年新高考数学第一轮复习课件:第45讲 随机抽样的方法、用样本估计总体,共27页。PPT课件主要包含了答案D,答案C,答案AC,答案BCD,答案360等内容,欢迎下载使用。
2024全国一轮数学(基础版)第54讲 正态分布课件PPT: 这是一份2024全国一轮数学(基础版)第54讲 正态分布课件PPT,共33页。PPT课件主要包含了链教材·夯基固本,激活思维,fx=,第2题,45%,基础回归,X~Nμσ2,x=μ,研题型·融会贯通,举题说法等内容,欢迎下载使用。
2024全国一轮数学(基础版)第27讲 复数课件PPT: 这是一份2024全国一轮数学(基础版)第27讲 复数课件PPT,共40页。PPT课件主要包含了链教材·夯基固本,激活思维,±3-4i,基础回归,a=c且b=d,研题型·融会贯通,举题说法,随堂内化等内容,欢迎下载使用。












