







所属成套资源:沪教五四版数学八年级上学期精品教学课件+作业(含答案)
- 沪教版五四制数学年八年级上册18.4《函数的表示法》(第1课时)精品教学课件+作业(含答案) 课件 11 次下载
- 沪教版五四制数学年八年级上册18.4《函数的表示法》(第2课时)精品教学课件+作业(含答案) 课件 10 次下载
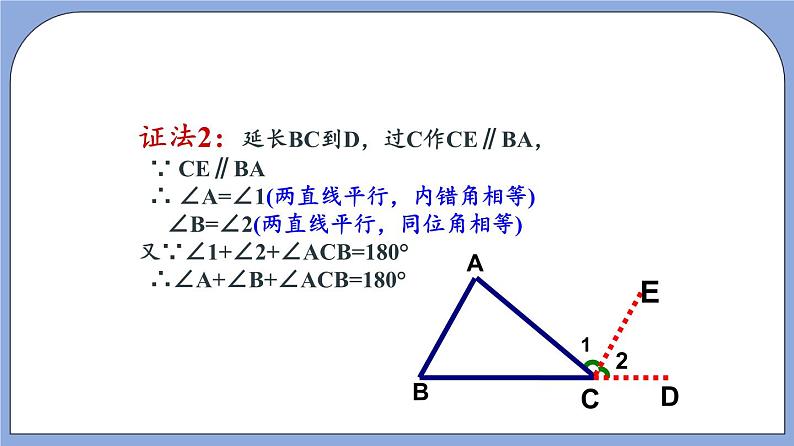
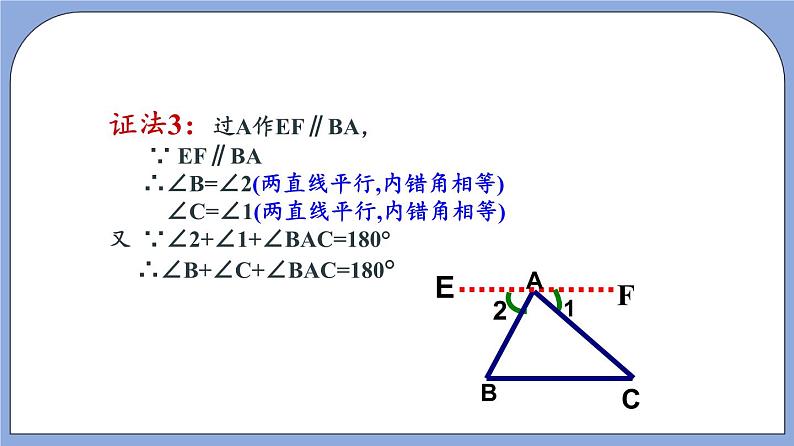
- 沪教版五四制数学年八年级上册19.2《证明举例—证明两条直线平行》(第1课时)精品教学课件+作业(含答案) 课件 10 次下载
- 沪教版五四制数学年八年级上册19.2《证明举例—证明线段和角相等》(第2课时)精品教学课件+作业(含答案) 课件 10 次下载
- 沪教版五四制数学年八年级上册19.2《证明举例—证明平行与线段之间数量关系》(第3课时)精品教学课件+作业(含答案) 课件 10 次下载
初中数学沪教版 (五四制)八年级上册19.1 命题和证明优质教学作业ppt课件
展开
这是一份初中数学沪教版 (五四制)八年级上册19.1 命题和证明优质教学作业ppt课件,文件包含191《命题和证明》教材配套课件pptx、191《命题和证明》作业夯实基础+能力提升解析版docx、191《命题和证明》作业夯实基础+能力提升原卷版docx等3份课件配套教学资源,其中PPT共38页, 欢迎下载使用。
19.1 命题和证明(作业)(夯实基础+能力提升)【夯实基础】一、单选题1.(2022·上海·八年级单元测试)下列说法正确的是( )A.命题一定有逆命题 B.所有的定理一定有逆定理C.真命题的逆命题一定是真命题 D.假命题的逆命题一定是假命题【答案】A【分析】根据命题的定义和定理及其逆定理之间的关系,分别举出反例,再进行判断,即可得出答案.【详解】解:A、命题一定有逆命题,故此选项符合题意;B、定理不一定有逆定理,如:全等三角形对应角相等没有逆定理,故此选项不符合题意;C、真命题的逆命题不一定是真命题,如:对顶角相等的逆命题是:相等的两个角是对顶角,它是假命题而不是真命题,故此选项不符合题意;D、假命题的逆命题定不一定是假命题,如:相等的两个角是对顶角的逆命题是:对顶角相等,它是真命题,故此选项不符合题意.故选:A.【点睛】本题考查了命题与定理,掌握好命题的真假及互逆命题的概念是解题的关键.把一个命题的条件和结论互换就得到它的逆命题,所有的命题都有逆命题;正确的命题叫真命题,错误的命题叫假命题.2.(2022·上海·八年级单元测试)下列命题中,真命题是( )A.同位角相等B.有两条边对应相等的等腰三角形全等C.互余的两个角都是锐角D.相等的角是对顶角.【答案】C【分析】根据平行线的性质、全等三角形的判定定理、余角的概念、对顶角的概念判断即可.【详解】解:A、两直线平行,同位角相等,故本选项说法是假命题;B、有两条边对应相等的等腰三角不一定形全等,故本选项说法是假命题;C、互余的两个角都是锐角,本选项说法是真命题;D、相等的角不一定是对顶角,例如,两直线平行,同位角相等,此时两个同位角不是对顶角,故本选项说法是假命题;故选:C.【点睛】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.3.(2021·上海同济大学附属存志学校八年级期中)设m是非零实数,给出下列四个命题:①若﹣1<m<0,则<m;②若m>1,<m;③若<m,则m>0;④若>m,则0<m<1,其中是真命题的是( )A.①② B.①③ C.②③ D.②④【答案】A【分析】根据不等式的性质,逐项判断,即可.【详解】解:①若﹣1<m<0,则<m,是真命题;②若m>1,<m,是真命题;③若<m,当 时, ,而 ,则原命题是假命题;④若>m,当 时, ,而 ,则原命题是假命题;则真命题有①②.故选:A【点睛】本题主要考查了命题的真假,熟练掌握一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可是解题的关键.4.(2022·上海·八年级单元测试)下列语句不是命题的是( )A.延长AB到D,使BD=2ABB.两点之间线段最短C.两条直线相交有且只有一个交点D.等角的补角相等【答案】A【分析】根据命题的概念判断即可.【详解】解:A、延长AB到D,使BD=2AB,没有对事情作出判断,不是命题,符合题意;B、两点之间线段最短,是命题,不符合题意;C、两条直线相交有且只有一个交点,是命题,不符合题意;D、等角的补角相等,是命题,不符合题意;故选:A.【点睛】本题考查的是命题的概念,判断一件事情的语句,叫做命题.5.(2021·上海市第四中学八年级阶段练习)下列命题中是真命题的( )A.一个角的两边与另一个角的两边分别平行,则这两个角相等B.在同一平面内,垂直于同一条直线的两条直线相互平行C.互补的两个角不是锐角就是钝角D.圆是轴对称图形,任何一条直径都是圆的对称轴【答案】B【分析】根据两边分别平行的两个角相等或互补对A进行判断;根据平行线的判断方法对B进行判断;据两个直角互补,不是锐角也不是钝角对C判断;根据对称轴的定义对B进行判断;【详解】A、一个角的两边与另一个角的两边分别平行,则这两个角相等或互补;所以A选项为假命题;B、在同一平面内,垂直于同一条直线的两条直线相互平行,所以B选项真命题;C、据两个直角互补,不是锐角也不是钝角;所以C选项为假命题;D、圆是轴对称图形,任何一条直径所在直线都是圆的对称轴,所以D选项为假命题.故选:B.【点睛】本题考查了命题与定理:命题写成“如果…,那么…”的形式,这时,“如果”后面接的部分是题设,“那么”后面解的部分是结论.命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.6.(2021·上海·八年级期中)下列命题中,真命题是( )A.全等三角形的对应边相等B.等腰三角形的对称轴是底边上的高C.两边及其中一边所对的角对应相等的两个三角形全等D.同位角相等【答案】A【分析】根据所学相关知识,逐一判断即可.【详解】∵全等三角形的对应边相等,∴A是真命题;∵等腰三角形的对称轴是底边上的高所在的直线,∴B是假命题;∵两边及其夹角对应相等的两个三角形全等,∴C是假命题;∵两直线平行,同位角相等,∴D是假命题;故选A.【点睛】本题考查了真命题,熟练掌握正确的数学性质,定义,定理,法则是解题的关键.7.(2020·上海市澧溪中学八年级阶段练习)下列命题中,属于真命题的是( )A.相等的角是对顶角; B.一个角的补角大于这个角C.内错角相等 D.一个三角形至少有两个内角是锐角【答案】D【分析】分析真假命题,需要分析题设是否能推出结论,根据对顶角的定义、补角定义、内错角定义、三角形的三角关系分别对各选项判断即可.【详解】解:A、不正确,因为对顶角相等,但相等的角不一定是对顶角;B、不正确,例如120°角的补角为60°,但60°小于120°;C、不正确,内错角不一定相等,缺少条件;D、正确,因为无论是锐角三角形、直角三角形还是钝角三角形都至少有两个角是锐角,故选:D.【点睛】本题考查了判定命题的的真假,涉及对顶角、内错角、补角、三角形的内角关系知识点,对各知识的灵活运用,利用排除法等方法判断命题的真假是解答的关键.8.(2021·上海·八年级专题练习)下列命题是真命题的是( )A.两个锐角的和还是锐角;B.全等三角形的对应边相等;C.同旁内角相等,两直线平行;D.等腰三角形既是轴对称图形,又是中心对称图形.【答案】B【分析】根据角的分类、全等三角形的性质、平行线的判定、轴对称图形和中心对称图形的定义逐一判断即可【详解】A、两锐角之和不一定是锐角,如40+80=120是钝角,故此选项错误;B、全等三角形的对应边相等,此选项正确;C、同旁内角互补,两直线平行,故同旁内角相等,两直线不一定平行,此选项错误;D、等腰三角形是轴对称图形,不是中心对称图形,此选项错误,故选:B【点睛】本题考查角的分类、全等三角形的性质、平行线的判定、轴对称图形和中心对称图形,熟练掌握相关知识是解答的关键9.(2021·上海·八年级期中)下列语句中,不是命题的是( )A.如果,那么、互为相反数B.同旁内角互补C.作等腰三角形底边上的高D.在同一平面内,若,则【答案】C【分析】根据命题的概念对每个选项一一判断正误即可.【详解】A、如果,那么、互为相反数,这句话是命题;B、同旁内角互补,这句话是命题;C、作等腰三角形底边上的高,这句话不是命题;D、在同一平面内,若,则,这句话是命题.故选:C.【点睛】本题主要考查命题的概念,熟记命题的概念是解题关键. 二、填空题10.(2021·上海·八年级专题练习)把命题“对顶角相等”改写成“如果……,那么……”的形式:______________.【答案】两个角是对顶角,那么这两个角相等【分析】先找到命题的题设和结论,再写成“如果…,那么…”的形式.【详解】解:把命题“对顶角相等”改写成“如果……,那么……”的形式为:如果两个角是对顶角,那么这两个角相等.故答案为:两个角是对顶角,那么这两个角相等【点睛】本题主要考查了将原命题写成条件与结论的形式,“如果”后面是命题的条件,“那么”后面是条件的结论,解决本题的关键是找到相应的条件和结论,比较简单.11.(2021·上海同济大学附属存志学校八年级期中)“三角形的一个外角大于任何一个内角”是 ___命题(填“真”或“假”).【答案】假【分析】利用举反例法,当三角形的一个内角为120°,则该角的外角为60°,而 ,即可求解.【详解】解:“三角形的一个外角大于任何一个内角”是假命题,理由如下:当三角形的一个内角为120°,则该角的外角为60°,而 ,即原命题为假命题.故答案为:假【点睛】本题主要考查了命题的真假,熟练掌握一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可是解题的关键.12.(2021·上海市川沙中学南校八年级期中)把命题“全等三角形对应边上的高相等”改写成“如果……,那……的形式为________.【答案】如果两个三角形全等,那么它们对应边上的高相等【分析】找出命题的条件和结论,在条件前加如果,在结论前加那么即可.【详解】解:把命题“全等三角形对应边上的高相等”改写成“如果……,那……的形式为是如果两个三角形全等,那么它们对应边上的高相等.故答案为如果两个三角形全等,那么它们对应边上的高相等.【点睛】此题考查命题的形式,解决的关键是掌握命题是由条件加结论组成.13.(2020·上海闵行·八年级期中)把命题“同位角相等,两直线平行”改写成“如果……那么……”的形式是________.【答案】如果两条直线被第三条直线所截且同位角相等,那么这两条直线平行【分析】一个命题都能写成“如果…那么…”的形式,如果后面是题设,那么后面是结论.【详解】解:“同位角相等,两直线平行”的条件是:“同位角相等”,结论为:“两直线平行”,所以写成“如果…,那么…”的形式为:“如果同位角相等,那么两直线平行”.故答案为:如果两条直线被第三条直线所截且同位角相等,那么这两条直线平行14.(2022·上海·八年级单元测试)把命题“同角的余角相等”改写成:如果_____________________,那么_____________.【答案】 两个角是同一个角的余角 这两个角相等【分析】根据命题的概念把原命题改写成“如果…,那么…”的形式,根据余角的概念判断即可.【详解】解:命题“同角的余角相等”,改写成“如果…,那么…”的形式为:如果两个角是同一个角的余角,那么这两个角相等.故答案为:两个角是同一个角的余角,这两个角相等.【点睛】本题考查的是命题的概念,命题写成“如果…,那么…”的形式,这时,“如果”后面接的部分是题设,“那么”后面解的部分是结论.15.(2021·上海·八年级专题练习)“有两角及其中一角的平分线对应相等的两个三角形全等”是_____命题.(填“真”或“假”)【答案】真【分析】将原命题写出已知和求证,然后进行证明后即可得到该命题为真命题.【详解】已知:△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,∠B、∠B′的角平分线,BD=B′D′,求证:△ABC≌△A′B′C′.证明:∵∠B=∠B′且∠B、∠B′的角平分线分别为BD和B′D′,∴∠ABD=∠A′B′D′=∠B,∵BD=B′D′,∠A=∠A′,∴△ABD≌△A′B′D′,∴AB=A′B′,∵∠A=∠A′,∠B=∠B′,∴△ABC≌△A′B′C′.∴“有两角及其中一角的平分线对应相等的两个三角形全等”是真命题,故答案为真.【点睛】本题考查命题与定理,解题的关键是掌握命题证明的基本步骤. 三、解答题16.(2020·上海市静安区实验中学八年级课时练习)如图,已知AC∥DE,∠1=∠2.求证AB∥CD.【答案】见解析【分析】由AC∥DE,根据“两直线平行,内错角相等”得到∠2=∠ACD,而∠1=∠2,则∠1=∠ACD,根据“内错角相等,两直线平行”即可得到结论.【详解】∵AC∥DE∴∠2=∠ACD∵∠1=∠2 ∴∠1=∠ACD∴AB∥CD【点睛】解答本题的关键是熟练掌握平行线的性质与判定:两直线平行,内错角相等;内错角相等,两直线平行. 【能力提升】一、单选题1.(2021·上海市奉贤区汇贤中学八年级期中)下列命题中,其命题是假命题是( )A.周长相等的两个三角形全等B.对顶角相等C.等边对等角D.两直线平行,同旁内角互补【答案】A【分析】对各个命题逐一判断后找到错误的即可确定假命题.【详解】解:A、周长相等的两个三角形不一定全等,是假命题;B、对顶角相等,是真命题;C、等边对等角,是真命题;D、两直线平行,同旁内角互补,是真命题;故选:A.【点睛】本题主要考查了命题与定理,熟练利用相关定理以及性质即可判定出命题正确性.2.(2021·上海·八年级专题练习)下列各命题中,假命题是( )A.有两边及其中一边上的中线对应相等的两个三角形全等B.有两边及第三边上高对应相等的两个三角形全等C.有两角及其中一角的平分线对应相等的两三角形全等D.有两边及第三边上的中线对应相等的两三角形全等【答案】B【分析】根据全等三角形的判定定理进行证明并依次判断.【详解】解:、有两边及其中一边上的中线对应相等的两个三角形全等,可利用证两步全等的方法求得,是真命题;、高有可能在内部,也有可能在外部,是不确定的,不符合全等的条件,原命题是假命题;、有两角及其中一角的平分线对应相等的两三角形全等,可利用证两步全等的方法求得,是真命题;、有两边及第三边上的中线对应相等的两三角形全等,可利用证两步全等的方法求得,是真命题;故选:.【点睛】此题考查全等三角形的判定定理:SSS、SAS、ASA、AAS、HL,灵活判定命题真假,熟记定理并灵活应用解决问题是解题的关键.3.(2021·上海·八年级专题练习)下列命题是真命题的是( )A.相等的两个角是对顶角B.好好学习,天天向上C.周长和面积相等的两个三角形全等D.两点之间线段最短【答案】D【分析】根据命题的定义以及几何知识逐一判断即可.【详解】解:A、相等的两个角不一定是对顶角,原命题是假命题;B、好好学习,天天向上,不是命题;C、周长和面积相等的两个三角形不一定全等,原命题是假命题;D、两点之间线段最短,是真命题;故选:D.【点睛】本题考查命题,掌握命题的定义以及对顶角的性质、全等三角形的判定、两点之间线段最短的基本事实是解题的关键.4.(2020·上海浦东新·八年级期末)下列命题的逆命题是假命题的是( )A.全等三角形的面积相等; B.等腰三角形两个底角相等;C.直角三角形斜边上的中线等于斜边的一半; D.在角的平分线上任意一点到这个角的两边的距离相等.【答案】A【分析】先确定每个命题的逆命题,再对每个选项依次判定即可解答.【详解】A.逆命题为:面积相等的三角形是全等三角形,是假命题,符合题意;B.逆命题为:两个角相等的三角形是等腰三角形,是真命题,不符合题意;C.逆命题为:一条边上的中线等于这条边的一半的三角形是直角三角形,是真命题,不符合题意;D.在角的内部到角的两边距离相等的点在这个角的平分线上,是真命题,不符合题意.故选:A.【点睛】此题考查命题,正确的命题是真命题,错误的命题是假命题,正确确定每个命题的逆命题是解此题的关键. 二、填空题5.(2021·上海市徐汇中学八年级期中)根据下图和命题“等腰三角形底边上的中线是顶角的角平分线”写出:已知:_______________________________求证:_______________ .【答案】 已知:△ABC中,AB=AC,AD是BC边上的中线 求证:AD平分∠BAC.【分析】结合几何图形写出已知条件和结论.【详解】已知:△ABC中,AB=AC,D为BC中点(或BD=DC);求证:AD平分∠BAC.故答案为△ABC中,AB=AC,D为BC中点(或BD=DC);AD平分∠BAC.【点睛】本题考查了命题与定理:命题写成“如果…,那么…”的形式,这时,“如果”后面接的部分是题设,“那么”后面解的部分是结论.6.(2021·上海·八年级期中)命题“等角对等边”改成“如果……,那么……”的形式:_____________【答案】在同一个三角形中,如果有两个角相等,那么这两个角所对的边也相等.【分析】分析原命题,找出其条件与结论,然后写成“如果…那么…”形式即可.【详解】解:因为条件是:在同一个三角形中,有两个角相等,结论为:这两个角所对的边也相等.所以改写后为:在同一个三角形中,如果有两个角相等,那么这两个角所对的边也相等.故答案为在同一个三角形中,如果有两个角相等,那么这两个角所对的边也相等.【点睛】本题考查命题的定义,难度适中,正确找到条件与结论是解题关键.7.(2020·上海市静安区实验中学八年级课时练习)把命题“直角三角形的两个锐角互为余角”改写成“如果…那么…”的形式是________,这个命题是__________(填“真”或“假”)命题【答案】 如果一个三角形是直角三角形,那么它的两个锐角互为余角 真【分析】找出命题中的题设与结论即可得,根据直角三角形的性质即可得判断真假.【详解】命题“直角三角形的两个锐角互为余角”中的题设是三角形是直角三角形,结论是它的两个锐角互为余角,则改写成:如果一个三角形是直角三角形,那么它的两个锐角互为余角,由直角三角形的性质得:这个命题是真命题,故答案为:如果一个三角形是直角三角形,那么它的两个锐角互为余角;真.【点睛】本题考查了命题、直角三角形的性质,掌握理解命题的概念是解题关键.8.(2020·上海市静安区实验中学八年级课时练习)等腰直角中,,,,,,则________.【答案】8【分析】先根据等腰直角三角形的定义可得,再根据直角三角形的性质可得,然后根据三角形全等的判定定理与性质可得,最后根据线段的和差即可得.【详解】是等腰直角三角形,且,,,,,,,在和中,,,,,,故答案为:8.【点睛】本题考查了等腰三角形的定义、直角三角形的性质、三角形全等的判定定理与性质等知识点,熟练掌握三角形全等的判定定理与性质是解题关键.9.(2020·上海市松江区民办茸一中学八年级阶段练习)把命题“直角三角形的两个锐角互余”改写成“如果……那么……”的形式:__________________.【答案】如果一个三角形是直角三角形,那么它的两个锐角互余【分析】首先找出原命题中的条件及结论,然后写成“如果…,那么…”的形式即可.【详解】解:把命题“直角三角形的两个锐角互余”改写成“如果……那么……”的形式为:如果一个三角形是直角三角形,那么它的两个锐角互余,故答案为:如果一个三角形是直角三角形,那么它的两个锐角互余.【点睛】本题考查命题,主要考查学生对命题的理解及运用能力.10.(2020·上海浦东新·八年级期中)把命题“等边对等角”改写成“如果…,那么…”的形式是:_____.【答案】如果三角形的两边相等,那么这两条边所对的角相等.【详解】试题分析:根据命题的定义改写即可.解:“等边对等角”改写为“如果三角形的两边相等,那么这两条边所对的角相等”.故答案为如果三角形的两边相等,那么这两条边所对的角相等.考点:命题与定理. 三、解答题11.(2022·上海·八年级单元测试)如图,直线、均被直线、所截,且与相交,给定以下三个条件:①;②;③;请从这三个条件中选择两个作为条件,另一个作为结论组成一个真命题,并进行证明已知:求证:证明:【答案】已知:,; 求证:,证明见解析【分析】如果选择①②两个作为条件,③作为结论可组成一个真命题.首先根据平行线的判定定理,可得,由,可得,然后,根据直角三角形的两个锐角互余及对顶角的性质,即可证明.【详解】已知:,,求证:.证明:,,,,,,.【点睛】本题主要考查了平行线的判定,直角三角形两锐角互余,对顶角的性质等等,熟知相关知识是解题的关键.12.(2020·上海市静安区实验中学八年级课时练习)已知:如图,AC⊥BC,垂足为C,∠BCD是∠B的余角求证:∠ACD=∠B证明:∵AC⊥BC(已知)∴∠ACB=90°( )∴∠BCD是∠DCA的余角∵∠BCD是∠B的余角(已知) ∴∠ACD=∠B( )【答案】垂直的意义;同角的余角相等.【分析】先根据垂直的意义可得,从而可得是的余角,再根据同角的余角相等即可得证.【详解】证明:∵(已知),∴(垂直的意义),∴是的余角,∵是的余角(已知),∴(同角的余角相等),故答案为:垂直的意义;同角的余角相等.【点睛】本题考查了垂直的意义、同角的余角相等,掌握理解同角的余角相等是解题关键.13.(2020·上海市静安区实验中学八年级课时练习)如图所示,与互补,.求证:.【答案】详见解析【分析】已知∠BAP与∠APD互补,根据同旁内角互补两直线平行,可得AB∥CD,再根据平行线的判定与性质及等式相等的性质即可得出答案.【详解】证明:∵∠BAP与∠APD互补,∴AB∥CD.∴∠BAP=∠APC,∵∠BAE=∠CPF,(已知)∴∠BAP-∠BAE=∠APC-∠CPF,即∠EAP=∠APE,∴AE∥FP.∴∠E=∠F.【点睛】本题考查了平行线的判定与性质,属于基础题,关键是正确理解与运用平行线的判定与性质.14.(2020·上海市静安区实验中学八年级课时练习)已知:如图,在中,FG∥EB,,那么等于多少度?为什么?解:=_______________.因为∥(______________________),所以(_________________________________).因为(已知),所以(_____________________).所以DE∥BC(_____________________).所以=_________(____________________).【答案】详见解析.【分析】根据平行线性质推出∠1=∠2,推出∠1=∠3,得出DE∥BC,根据平行线的性质推出即可.【详解】∠EDB+∠DBC= 180º . 因为FG∥EB(已知),所以∠1=∠2 (两直线平行,同位角相等).因为∠2=∠3(已知),所以∠1=∠3(等量代换). 所以DE∥BC(内错角相等,两直线平行). 所以∠EDB+∠DBC=180º(两直线平行,同旁内角互补).【点睛】本题考查了平行线性质和判定的应用,主要考查学生的推理能力.
相关课件
这是一份初中数学沪教版 (五四制)八年级上册19.10 两点的距离公式优质教学作业课件ppt,文件包含1910《两点的距离公式》教材配套课件pptx、1910《两点的距离公式》作业解析版docx、1910《两点的距离公式》作业原卷版docx等3份课件配套教学资源,其中PPT共15页, 欢迎下载使用。
这是一份沪教版 (五四制)八年级上册19.6 轨迹优质教学作业ppt课件,文件包含196《轨迹》第1课时教材配套课件pptx、196《轨迹》第1课时作业解析版docx、196《轨迹》第1课时作业原卷版docx等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
这是一份数学沪教版 (五四制)19.1 命题和证明优质课件ppt,文件包含沪教版数学八上191《命题和证明》课件ppt、沪教版数学八上191《命题和证明》教案doc等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。











