沪教版 (五四制)八年级上册19．9 勾股定理一等奖教学作业ppt课件

这是一份沪教版 (五四制)八年级上册19．9 勾股定理一等奖教学作业ppt课件，文件包含199《勾股定理》第3课时教材配套课件pptx、199《勾股定理》第3课时作业解析版docx、199《勾股定理》第3课时作业原卷版docx等3份课件配套教学资源，其中PPT共23页， 欢迎下载使用。
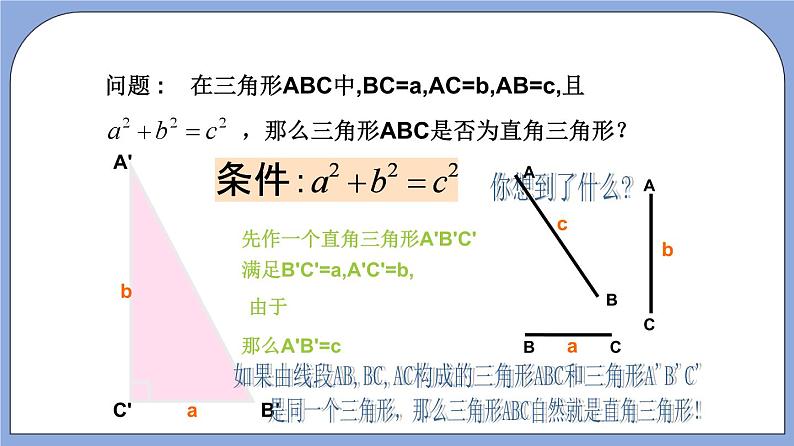
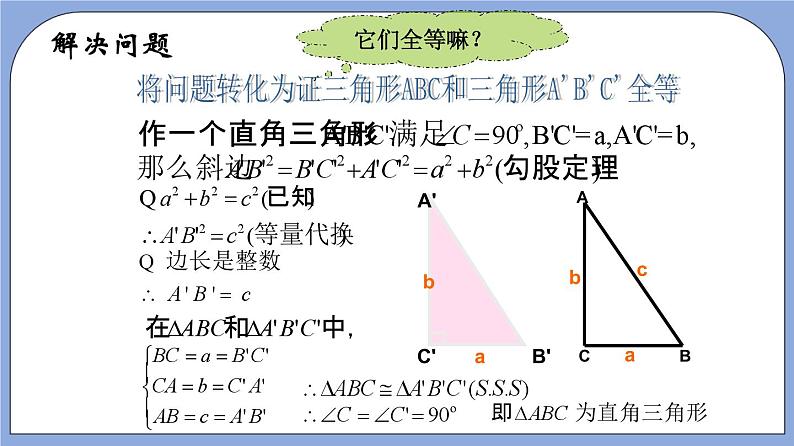
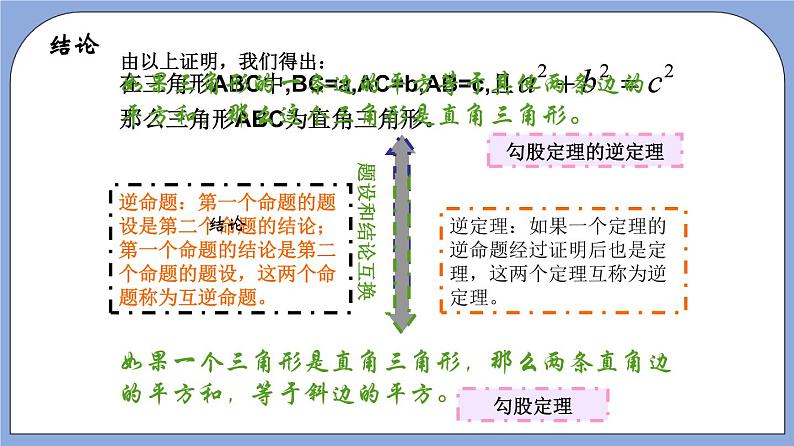
19.9勾股定理（第3课时）（作业）【夯实基础】一、单选题1．（2022·上海·八年级单元测试）下列数据不是勾股数的是（　　）A．7，14，16 B．5，12，13 C．3，4，5 D．9，40，412．（2021·上海市洋泾菊园实验学校八年级期末）用下列几组边长构成的三角形中哪一组不是直角三角形（　　）A．8，15，17 B．6，8，10 C． D．3．（2019·上海市建平中学西校八年级阶段练习）已知a、b、c分别是△ABC的三边,根据下列条件能判定△ABC为直角三角形的是（      ）A．a=8,b=13,c=11 B．a=6,b=10,c=12C．a=40,b=4l,c=9 D．a=24,b=9,c=254．（2020·上海浦东新·八年级期末）在△ABC中，BC＝6，AC＝8，AB＝10，则该三角形为（　　）A．锐角三角形 B．直角三角形C．钝角三角形 D．等腰直角三角形5．（2019·上海市进才中学北校八年级阶段练习）以下列各组数为边长的三角形中，能够构成直角三角形的是（      ）A．32,42,52； B．2，，；C．； D．，，6．（2022·上海徐汇·八年级期末）满足下列条件的三角形中，不是直角三角形的是（    ）A．三内角之比为3：4：5 B．三边长的平方之比为1：2：3C．三边长之比为7：24：25 D．三内角之比为1：2：37．（2022·上海·八年级单元测试）在下列四个条件：①，②，③，④中，能确定是直角三角形的条件有（    ）．A．①③ B．①②③ C．①②④ D．①②③④  8．（2021·上海市南汇第四中学八年级期末）在中，，，，AD平分交BC于点D，那么点D到AB的距离是（    ）A．4.8 B．4 C．3 D．二、填空题9．（2022·上海·八年级单元测试）如图，在4×3的正方形网格中，△ABC与△DEC的顶点都在边长为1的小正方形的顶点上，则∠BAC+∠CDE＝___度．10．（2021·上海·八年级专题练习）已知直角坐标平面内的点，和，那么的形状是______．11．（2017·上海市中国中学八年级阶段练习）若一个三角形的三边长分别为5，12，13，则此三角形的最长边上的高为_____．三、解答题12．（2021·上海虹口·八年级期末）如图，Rt△ABC中，∠ACB＝90°，分别以AC，BC，AB为边作正方形，面积分别记作S1、S2、S3．求证：S1+S2＝S3．    13．（2019·上海市建平中学西校八年级阶段练习）在四边形ABCD 中，AD⊥CD，AB=12，BC=13，CD=3，AD=4，求 S四边形ABCD   14．（2018·上海·八年级期中）如图四边形ABCD是一块草坪，量得四边长AB=3m，BC=4m，DC=12m，AD=13m，∠B=90°，求这块草坪的面积．    【能力提升】一、单选题1．（2022·上海浦东新·八年级期末）下列三个数为边长的三角形不是直角三角形的是（    ）A．3，3， B．4，8， C．6，8，10 D．5，5，2．（2021·上海·八年级专题练习）下列四组数据为三角形的三边，其中能构成直角三角形的是（      ）A．； B．； C．； D．．3．（2021·上海市南汇第四中学八年级期末）在中，、、的对应边分别是a、b、c，下列条件中不能说明是直角三角形的是（    ）A． B．C． D．二、填空题4．（2022·上海·八年级专题练习）如图，在四边形ABCD中，AB：BC：CD：DA=2：2：3：1，且∠ABC=90°，则∠DAB的度数是______°．5．（2022·上海市风华初级中学八年级期末）如图，在△ABC中，AB=6，BC=10，AC=8，点D是BC的中点，如果将△ACD沿AD翻折后，点C的对应点为点E，那么CE的长等于________.6．（2022·上海·八年级期末）如图，在四边形ABCD中，AD=，AB=，BC=10，CD=8，∠BAD=90°，那么四边形ABCD的面积是___________．7．（2022·上海·八年级期末）已知一个三角形三边的长分别为，则这个三角形的面积是_________________．      三、解答题8．（2022·上海·八年级专题练习）如图是一块四边形绿地的示意图，其中，，，，．求此绿地的面积．9．（2022·上海·八年级专题练习）如图，在四边形ABCD中，AB＝BC＝2，CD＝3，AD＝1，且∠ABC＝90°，试求∠A的度数． 10．（2022·上海·八年级专题练习）如图，已知直线与双曲线在第一象限交于点，且点的横坐标为4，点在双曲线上. （1）求双曲线的函数解析式；（2）若点的纵坐标为8，试判断形状，并说明理由.   11．（2020·上海市奉贤区弘文学校八年级期末）如图，已知四边形ABCD中，AB=24，AD=15，BC=20，CD=7，∠ADB+∠CBD=90°．（1）在BD的上方作△A'BD，使△A'BD≌△ADB（点A与点不重合）（不写作法，保留作图痕迹）；（2）求四边形ABCD的面积．   12．（2022·上海浦东新·八年级期末）如图，中，，，．点P是射线CB上的一点（不与点B重合），EF是线段PB的垂直平分线，交PB与点F，交射线AB与点E，联结PE、AP．（1）求的度数；（2）当点P在线段CB上时，设，的面积为y，求y关于x的函数解析式，并写出函数的定义域；（3）如果，请直接写出的面积．