人教版八年级上册第十三章 轴对称13.3 等腰三角形13.3.1 等腰三角形获奖课件ppt

这是一份人教版八年级上册第十三章 轴对称13.3 等腰三角形13.3.1 等腰三角形获奖课件ppt，共17页。PPT课件主要包含了知识回顾，学习目标，课堂导入，新知探究，跟踪训练，CEDA，∠A∠B，随堂练习，ABDC，OAOB等内容，欢迎下载使用。

等腰三角形的性质1：等腰三角形的两个底角相等（简写成“等边对等角”）.
等腰三角形的性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合（简写成“三线合一”）.
等腰三角形有哪些性质？
1.理解等腰三角形的判定，体会等腰三角形“等边对等角”和“等角对等边”的区别.2.探索并掌握等腰三角形的判定的过程，并用以解决实际问题.
我们知道，如果有一个三角形有两条边相等，那么它们所对的角相等.反过来，如果一个三角形有两个角相等，那么它们所对的边有什么关系？
证明：如图，作∠BAC的平分线AD交BC于点D， ∴∠BAD=∠CAD.∵在△ABD和△ACD中， ∠B=∠C， ∠BAD=∠CAD， AD=AD，∴△ABD≌△ACD（AAS）.∴ AB=AC.
如图，在△ABC中， ∠B=∠C.求证：AB=AC.
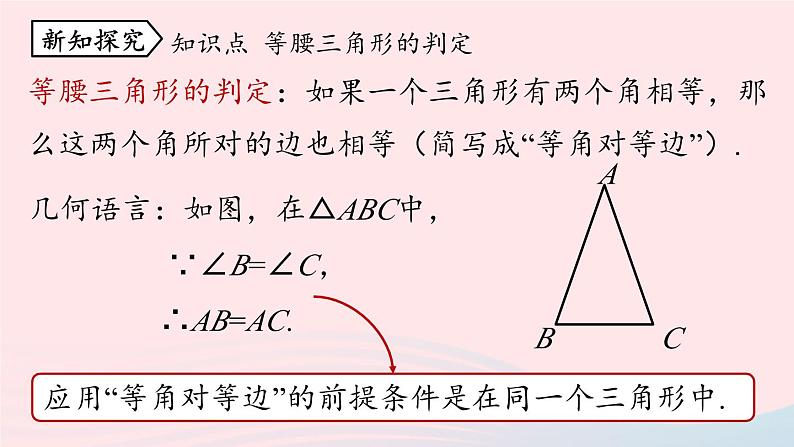
等腰三角形的判定：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）.
几何语言：如图，在△ABC中， ∵∠B=∠C， ∴AB=AC.
知识点 等腰三角形的判定
例1 求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形.
分析：命题的证明首先需要将命题转化为已知、求证的格式，再要根据题意画出图形，最后证明结论的成立.
已知：∠CAE是△ABC的外角，∠1=∠2，AD//BC.求证：AB=AC.
证明：∵AD//BC， ∴∠1=∠B,∠2=∠C.∵∠1=∠2，∴∠B=∠C，∴AB=AC.
AB//CD，∠1=∠2
作法：（1）作线段AB=a.（2）作线段AB的垂直平分线MN，与AB相交于点D.（3）在MN上取一点C，使得DC=h.（4）连接AC，BC.则△ABC就是所求作的等腰三角形.
例2 已知等腰三角形底边长为a，底边上的高的长为h，求作这个等腰三角形.
解：∵在△ABC中，∠A=36°，∠C=72°，∴∠ABC=72°.∵∠DBC=36°， ∴∠2=∠ABC-∠DBC=36°.∵∠1=∠A+∠2=72°，∴AD=BD=BC，AB=AC.图中的等腰三角形有△ABC，△ABD，△BCD.
如图,∠A=36°,∠DBC=36°,∠C=72°,分别计∠1,∠2的度数,并说明图中有哪些等腰三角形.
1.如图，∠A=∠B，CE//DA，CE交AB于点E.求证：△CEB是等腰三角形.
证明：∵CE//DA， ∴∠A=∠CEB. ∵∠A=∠B， ∴∠CEB=∠B. ∴CE=CB，则△CEB是等腰三角形.
2.如图，AC和BD相交于点O，且AB//DC，OA=OB.求证：OC=OD.
证明：∵AB//DC，∴∠A=∠C，∠B=∠D.∵OA=OB，∴∠A=∠B，则∠C=∠D.∴OC=OD.
3.如图，AD//BC，BD平分∠ABC.求证：AB=AD.
证明：∵BD平分∠ABC,∴∠ABD=∠CBD. ∵AD//BC，∴∠ADB=∠CBD.∴∠ABD=∠ADB. ∴AB=AD.
如果一个三角形有两个角相等，那么这两个角所对的边也相等
将等腰三角形的性质和判定综合应用在解决实际问题中
如图，在△ABC中，BA=BC，点D是AB延长线上一点，DF⊥AC于点F，交BC于点E.求证：△DBE是等腰三角形.