




还剩11页未读,
继续阅读
所属成套资源:人教版数学八上PPT课件整套【2024秋季新】
成套系列资料,整套一键下载
- 人教版数学八上 11.1.1 三角形的边 课件 课件 19 次下载
- 人教版数学八上 11.1.3 三角形的稳定性 课件 课件 17 次下载
- 人教版数学八上 11.2.1 三角形的内角 课件 课件 22 次下载
- 人教版数学八上 11.2.2 三角形的外角 课件 课件 26 次下载
- 人教版数学八上 11.3.1 多边形 课件 课件 23 次下载
人教版数学八上 11.1.2 三角形的高、中线与角平分线 课件
展开
这是一份人教版数学八上 11.1.2 三角形的高、中线与角平分线 课件,共19页。
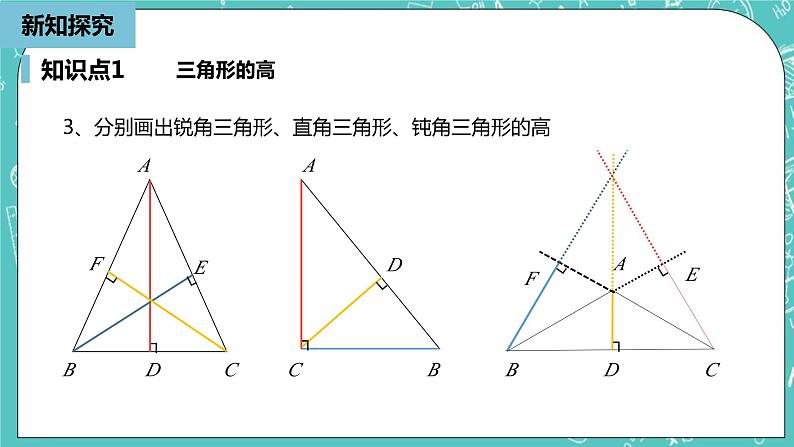
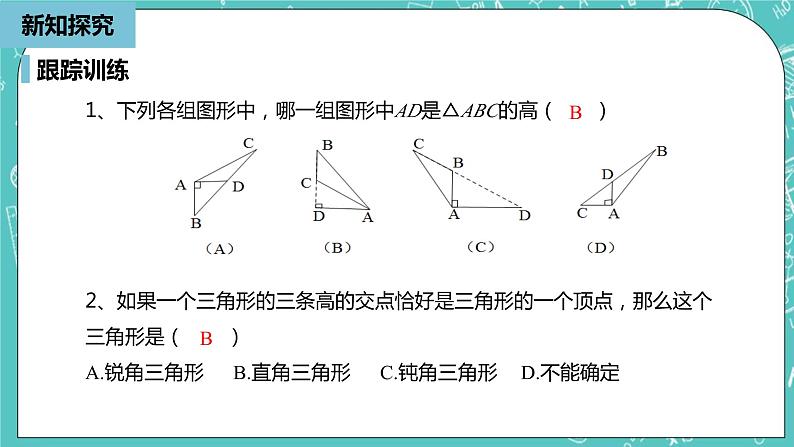
11.1.2 三角形的高、中线与角平分线人教版数学八年级上册知识回顾知识回顾想一想,议一议我们已经学过三角形的高,还有哪些和三角形有关的线段?三角形的分类三角形的三边关系学习目标 1.了解三角形的高、中线和角平分线的定义及画法. 2.掌握三角形的高、中线和角平分线的性质. 3.会利用三角形的三种线段性质来解决实际问题.课堂导入你还记得小学学过的“三角形的高”的定义吗?定义:从三角形的一个顶点向它所对的边所在的直线画垂线,顶点和垂足之间的线段叫做三角形的这条边上的高,这条对边叫做三角形的底.C知识点1新知探究1、表示方法:从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高. 记作AD⊥BC于点D.2、三角形高的画法用三角板过某一顶点向其对边或对边所在的直线画垂线,交对边或对边延长线于一点,所得的垂线段就是这条边上的高.三角形的高BCA┐D知识点1新知探究3、分别画出锐角三角形、直角三角形、钝角三角形的高三角形的高B┐┐┐┐┐┐┐┐知识点1新知探究三角形的高总结:(1)锐角三角形的三条高都在内部,三条高的交点也在内部. (2)直角三角形的两条高与直角边重合,另外一条高在内部,三条高的交点为直角顶点. (3)钝角三角形的两条高在外部,另外一条高在内部,三条高没有交点,三条高所在直线交于三角形外一点.2、如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定跟踪训练新知探究BB新知探究新知探究知识点2三角形的中线1、定义:连接三角形的一个顶点和它所对的边的中点,所得线段叫做三角形的这条边上的中线.新知探究新知探究知识点23、重心:三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.三角形的中线新知探究新知探究知识点2三角形的中线如图,在△ABC中,AD,AE分别是边BC的中线和高,试比较△ABD和△ACD的面积大小.新知探究新知探究跟踪训练1、如图,有一块三角形的菜地,现要求分成面积比为1:1:2三块,且图中A处是三块菜地的共同水源处,应该怎么分? 解:根据面积比值为1:1:2的要求,可以将三角形菜地的总面积看作4份.利用三角形的中线可以将三角形分成面积相等的两个小三角形的性质. 如图,分别作出两条中线,所得到的△ABE,△AED,△ADC的面积之比就是1:1:2.ABCED新知探究新知探究知识点31、定义:画∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫做△ABC的角平分线.三角形的角平分线新知探究新知探究ABCEF1234(1)∠1=∠( );(2)∠3= ( );(3)∠ACB=( )∠4.2∠ABC解析:利用三角形的角平分线的性质进行解答.2跟踪训练随堂练习1如图,在△ABC中,AE是中线,AD是角平分线,AF是高,填空:(1)BE=( )= ( ); (2)∠BAD=( )= ( ); (3)∠AFB=( )=90°;(4)当BE=8,AF=7时,求△ABC的面积. 解:因为AE为中线,所以点E为BC的中点,BE=CE= BC. 因为AD为角平分线,所以∠BAD=∠CAD= ∠BAC. 因为AF为高,所以∠AFB=∠CFA=90°. 因为BE=8,所以BC=16,△ABC的面积为 ×16×7=56.CEBC∠CAD∠BAC∠CFA随堂练习2如图,在△ABC中,∠ACB=90°,把△ABC沿AC翻折180°,使得点B落在点B1的位置,则线段AC具有的性质是( )B1A.是边BB1上的中线 B.是边BB1上的高C.是∠BAB1的角平分线 D.以上三种性质合一解:∵△ABC翻折得到△AB1C, ∴BC=B1C,∠ACB=∠ACB1=90°, ∠BAC=∠B1AC.D随堂练习3本题源于《教材帮》解:∵△ABC的周长为AB+BC+AC=27cm,AC=9cm, ∴AB+BC=18cm. (1) ∵△ABD的周长为AB+BD+AD=19cm,AD=6cm, ∴AB+BD=13cm. (2) ∵BC边上的中线为AD, ∴BC=2BD. (1)-(2)得:BD=5cm,∴AB=8cm.如图所示,已知△ABC的周长为27cm,AC=9cm,BC边上的中线AD为6cm,△ABD的周长为19cm,AB=______.8cm课堂小结垂直关系,90°的角按角分类的三角形,三条高的交点位置拓展提升1如图,在△ABC中,AD⊥BC,AE平分∠BAC(∠B>∠C). 若∠B=80°,∠C=30°,求∠DAE.解:∵在△ABC中, ∠B=80°,∠C=30°, ∴∠BAC=70°. ∵AE平分∠BAC, ∴∠BAC=2∠BAE=2∠CAE. ∵∠BAC=70°, ∴∠BAE=35°. ∵AD⊥BC,∠B=80°, ∴∠BAD=10°. ∴ ∠DAE=∠BAE-∠BAD=35°-10°=25°.
11.1.2 三角形的高、中线与角平分线人教版数学八年级上册知识回顾知识回顾想一想,议一议我们已经学过三角形的高,还有哪些和三角形有关的线段?三角形的分类三角形的三边关系学习目标 1.了解三角形的高、中线和角平分线的定义及画法. 2.掌握三角形的高、中线和角平分线的性质. 3.会利用三角形的三种线段性质来解决实际问题.课堂导入你还记得小学学过的“三角形的高”的定义吗?定义:从三角形的一个顶点向它所对的边所在的直线画垂线,顶点和垂足之间的线段叫做三角形的这条边上的高,这条对边叫做三角形的底.C知识点1新知探究1、表示方法:从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高. 记作AD⊥BC于点D.2、三角形高的画法用三角板过某一顶点向其对边或对边所在的直线画垂线,交对边或对边延长线于一点,所得的垂线段就是这条边上的高.三角形的高BCA┐D知识点1新知探究3、分别画出锐角三角形、直角三角形、钝角三角形的高三角形的高B┐┐┐┐┐┐┐┐知识点1新知探究三角形的高总结:(1)锐角三角形的三条高都在内部,三条高的交点也在内部. (2)直角三角形的两条高与直角边重合,另外一条高在内部,三条高的交点为直角顶点. (3)钝角三角形的两条高在外部,另外一条高在内部,三条高没有交点,三条高所在直线交于三角形外一点.2、如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定跟踪训练新知探究BB新知探究新知探究知识点2三角形的中线1、定义:连接三角形的一个顶点和它所对的边的中点,所得线段叫做三角形的这条边上的中线.新知探究新知探究知识点23、重心:三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.三角形的中线新知探究新知探究知识点2三角形的中线如图,在△ABC中,AD,AE分别是边BC的中线和高,试比较△ABD和△ACD的面积大小.新知探究新知探究跟踪训练1、如图,有一块三角形的菜地,现要求分成面积比为1:1:2三块,且图中A处是三块菜地的共同水源处,应该怎么分? 解:根据面积比值为1:1:2的要求,可以将三角形菜地的总面积看作4份.利用三角形的中线可以将三角形分成面积相等的两个小三角形的性质. 如图,分别作出两条中线,所得到的△ABE,△AED,△ADC的面积之比就是1:1:2.ABCED新知探究新知探究知识点31、定义:画∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫做△ABC的角平分线.三角形的角平分线新知探究新知探究ABCEF1234(1)∠1=∠( );(2)∠3= ( );(3)∠ACB=( )∠4.2∠ABC解析:利用三角形的角平分线的性质进行解答.2跟踪训练随堂练习1如图,在△ABC中,AE是中线,AD是角平分线,AF是高,填空:(1)BE=( )= ( ); (2)∠BAD=( )= ( ); (3)∠AFB=( )=90°;(4)当BE=8,AF=7时,求△ABC的面积. 解:因为AE为中线,所以点E为BC的中点,BE=CE= BC. 因为AD为角平分线,所以∠BAD=∠CAD= ∠BAC. 因为AF为高,所以∠AFB=∠CFA=90°. 因为BE=8,所以BC=16,△ABC的面积为 ×16×7=56.CEBC∠CAD∠BAC∠CFA随堂练习2如图,在△ABC中,∠ACB=90°,把△ABC沿AC翻折180°,使得点B落在点B1的位置,则线段AC具有的性质是( )B1A.是边BB1上的中线 B.是边BB1上的高C.是∠BAB1的角平分线 D.以上三种性质合一解:∵△ABC翻折得到△AB1C, ∴BC=B1C,∠ACB=∠ACB1=90°, ∠BAC=∠B1AC.D随堂练习3本题源于《教材帮》解:∵△ABC的周长为AB+BC+AC=27cm,AC=9cm, ∴AB+BC=18cm. (1) ∵△ABD的周长为AB+BD+AD=19cm,AD=6cm, ∴AB+BD=13cm. (2) ∵BC边上的中线为AD, ∴BC=2BD. (1)-(2)得:BD=5cm,∴AB=8cm.如图所示,已知△ABC的周长为27cm,AC=9cm,BC边上的中线AD为6cm,△ABD的周长为19cm,AB=______.8cm课堂小结垂直关系,90°的角按角分类的三角形,三条高的交点位置拓展提升1如图,在△ABC中,AD⊥BC,AE平分∠BAC(∠B>∠C). 若∠B=80°,∠C=30°,求∠DAE.解:∵在△ABC中, ∠B=80°,∠C=30°, ∴∠BAC=70°. ∵AE平分∠BAC, ∴∠BAC=2∠BAE=2∠CAE. ∵∠BAC=70°, ∴∠BAE=35°. ∵AD⊥BC,∠B=80°, ∴∠BAD=10°. ∴ ∠DAE=∠BAE-∠BAD=35°-10°=25°.
相关资料
更多









