人教版九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定公开课ppt课件

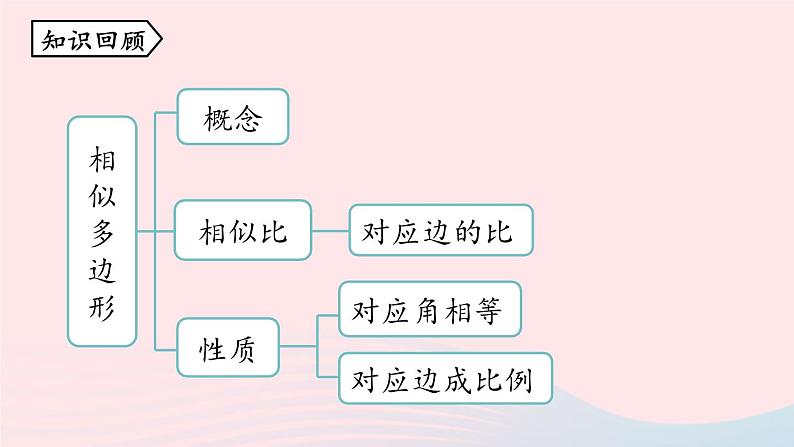
这是一份人教版九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定公开课ppt课件，共34页。PPT课件主要包含了相似多边形，相似比，对应角相等，对应边成比例，知识回顾，对应边的比，学习目标，课堂导入，知识点1相似三角形，新知探究等内容，欢迎下载使用。
1.理解相似三角形的概念，体会用相似符号“∽”表示的相似三角形之间的边，角对应关系.
2. 掌握平行线分线段成比例的基本事实及其推论.
3.掌握平行线分线段成比例的基本事实及其推论的应用,会用平行线判定两个三角形相似并进行证明和计算.
判定两个三角形全等时，除了可以验证它们所有的角和边分别相等外，还可以使用简便的判定方法(SSS，SAS，ASA，AAS).类似地，判定两个三角形相似时，是不是也存在简便的判定方法呢？
如图，在△ABC 和△DEF 中，如果
注意：用符号“∽”表示两个三角形相似时，要把表示对应顶点的大写字母写在对应的位置上. △ABC∽△DEF 表示顶点 A 与 D，B 与 E，C 与 F分别对应.；如果仅说“△ABC与△DEF相似 ”，没有用“∽”连接，则需要分类讨论它们之间的对应关系。
(1)相似三角形的定义可以作为相似三角形的判定方法，也是相似三角形最重要的性质.(2)全等三角形是特殊的相似三角形，即全等三角形是相似比为1的相似三角形，而相似三角形不一定是全等三角形.(3)相似三角形具有传递性,即若△ABC∽ △DEF， △DEF∽ △OPQ，则△ABC∽ △OPQ.
如图①，小方格的边长都是1，直线 a∥b∥c，分别交直线 m，n 于A1，A2，A3，B1，B2，B3.
知识点2：平行线分线段成比例
(1) 计算 ，你有什么发现？
(2) 将直线 b 向下平移到如图②的位置，直线 m，n 与直线 b 的交点分别为 A2，B2. 你在问题 (1) 中发现的结论还成立吗？如果将 b 平移到其他位置呢？
(3) 根据前两问，你认为在平面上任意作三条平行线，用它们截两条直线，截得的对应线段成比例吗？
平行线分线段成比例的基本事实：两条直线被一组平行线所截，所得的对应线段成比例.
1.对应线段是指被两条平行线所截得的线段，如上图中的 A1A2 与B1B2 是对应线段，A2A3与 B2B3是对应线段，A1A3 与 B1B3 是对应线段.2.对应线段成比例是指同一条直线上的两条线段的比，等于另一条直线上与它们对应的线段的比，书写时，要把对应线段写在对应的位置上.3.基本事实中的“所得的对应线段”是指被截直线上的线段，与这组平行线上的线段无关.
如图，直线 a∥b∥c，由平行线分线段成比例的基本事实，我们可以得出图中对应成比例的线段.
把直线 n 向左或向右任意平移，这些线段依然成比例.
直线 n 向左平移到 B1 与 A1 重合的位置，说说图中有哪些成比例线段？
把图中的部分线擦去，得到新的图形，刚刚所说的线段是否仍然成比例？
直线 n 向左平移到 B2 与A2 重合的位置，说说图中有哪些成比例线段？
如图，在△ABC 中，D 为 AB 上任意一点，过点 D 作 BC 的平行线 DE，交 AC 于点 E.
△ADE 与△ABC 的三个角分别相等吗？为什么？
知识点3：利用平行线判定两个三角形相似的定理
相等.理由如下：在 △ADE 与 △ABC 中，∠A=∠A.∵ DE∥BC，∴ ∠ADE=∠B，∠AED=∠C.
那么△ADE 与△ABC 的对应边长是否成比例呢？该怎么证明呢？
成比例.证明：如图，过点 D 作 DF∥AC，交 BC 于点 F.
∵ DE∥BC，DF∥AC，
∵ 四边形DFCE为平行四边形，
通过以上结论，你发现△ADE 与△ABC 之间有什么关系？平行移动DE 的位置，结论还成立吗？
定理：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.
几何语言：如下图所示，∵DE//BC，∴△ADE∽△ABC.
注意：定理中“和其他两边相交”是指和其他两边所在的直线相交.
三角形相似的两种常见类型：
如图，AB//EF//DC，AD//BC，EF 与 AC 交于点 G，则图中的相似三角形共有( )A.3对B.5对C.6对D.8对
△AEG ∽△ADC,△AEG ∽ △CFG,△AEG ∽△CBA,△ADC∽△CFG,△ADC ∽△CBA,△CFG∽△CBA.
2.如图， l1 //l2//l3，AB=3，AD=2，DE=4，EF=7.5，求 BC，BF 的长.
3.如图，在△ABC 中，点 D，E 分别是 AB，AC 上的点，且 AB=3AD，E 是 AC 的中点，DE 的延长线交 BC 延长线于点 F.求证：BC=CF.
解：如图， 过点 C 作 CG//DE，交 AB 于点 G.
1.(2021•烟台中考)《九章算术》中记载了一种测量古井水面以上部分深度的方法．如图所示，在井口A处立一根垂直于井口的木杆AB，从木杆的顶端B观察井水水岸D，视线BD与井口的直径AC交于点E，如果测得AB＝1米，AC＝1.6米，AE＝0.4米，那么CD为___米．
2.(2021•宿迁中考)如图，在△ABC中，AB＝4，BC＝5，点D，E分别在BC，AC上，CD＝2BD，CE＝2AE，BE交AD于点F，则△AFE面积的最大值是 _______．
CD＝2BD,CE＝2AE
当AB⊥BC时，△ABD的面积最大
3.(黄冈中考)如图，在Rt△ABC 中，∠ACB =90°，以 AC 为直径的⊙O 交 AB 于点 D.过点 D 作⊙O 的切线交 BC 于点 E，连接 OE.(1)求证：△DBE 是等腰三角形；
证明：(1)连接OD，如图所示.
∵ DE 是⊙O 的切线,
∴ ∠ODE =90°,
∴ ∠ADO+∠BDE = 90°.
∵ ∠ACB =90°,
∴ ∠CAB +∠CBA = 90°.
∴ ∠CAB = ∠ADO，
∴ ∠BDE =∠CBA，
∴ △DBE是等腰三角形.