2023届河南省实验中学高三数学（文）全真模拟一试题含解析

这是一份2023届河南省实验中学高三数学（文）全真模拟一试题含解析，共20页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
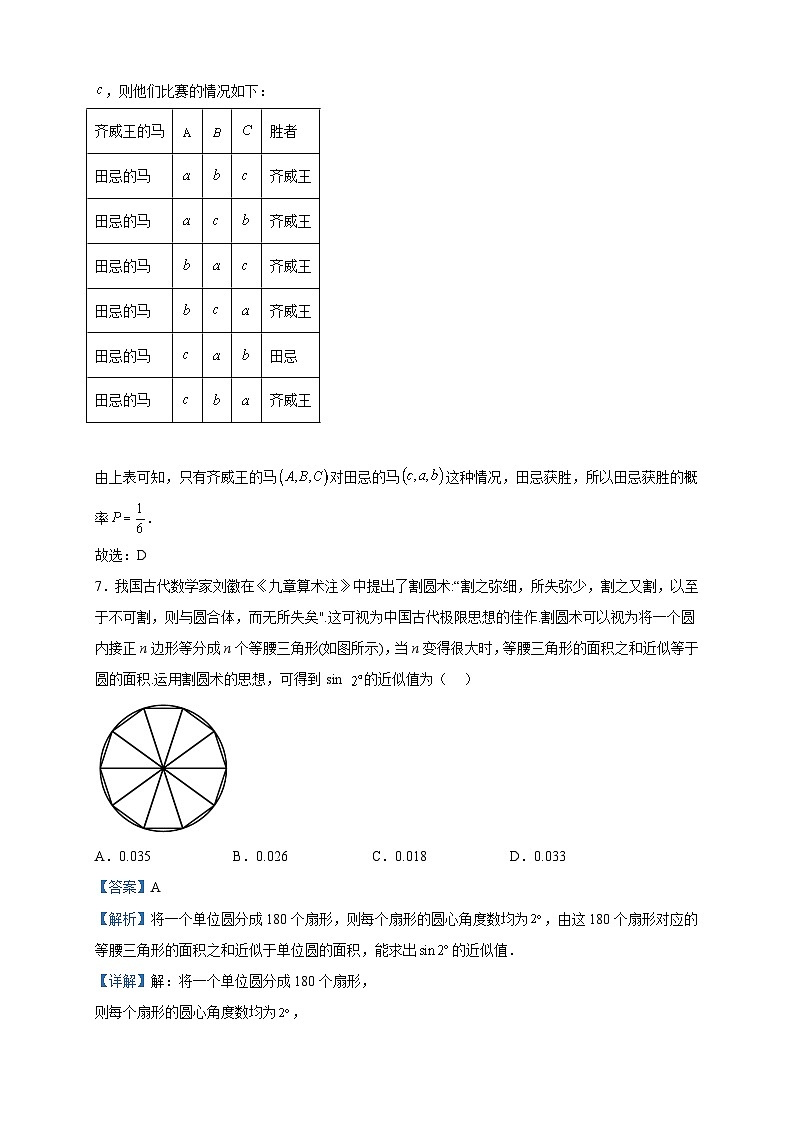
2023届河南省实验中学高三数学（文）全真模拟一试题 一、单选题1．已知集合，，则（    ）A． B． C． D．【答案】B【分析】根据二次不等式与根式的定义域求解，再取交集即可.【详解】，，故.故选：B2．已知复数，则（    ）A． B． C． D．【答案】A【分析】根据复数的除法运算化简，可得与.【详解】，，，所以，故选：A.3．设命题，则的否定为（    ）A． B．C． D．【答案】C【分析】根据含有量词的命题否定方法求解.【详解】因为命题，所以的否定为：.故选：C.4．已知代表不同的平面，代表不同的直线，则下列说法中正确的是（    ）A．若，则B．若，则C．若，则D．若，则【答案】D【分析】利用空间线面的关系，对四个选项一一判断即可.【详解】对于A：若，则与平面可能平行，也可能垂直，也可能斜交.故A错误；对于B：若，则可能平行，也可能相交，也可能异面.故B错误；对于C：若，则可能平行，也可能异面.故C错误；对于D：若，则.又，所以.故D正确.故选：D5．已知单位向量，满足，若向量，则（    ）A． B． C． D．【答案】B【分析】根据向量的数量积运算以及夹角的余弦公式，可得答案.【详解】由单位向量，则，即，，.故选：B.6．齐国的大将田忌很喜欢赛马，他与齐威王进行赛马比赛，他们都各有上、中、下等马各一匹，每次各出一匹马比一场，比赛完三场（每个人的三匹马都出场一次）后至少赢两场的获胜．已知同等次的马，齐威王的要强于田忌的，但是不同等次的马，都是上等强于中等，中等强于下等，如果两人随机出马，比赛结束田忌获胜的概率为（    ）A． B． C． D．【答案】D【分析】列举出各种对应情况，由概率公式即可得到答案.【详解】将齐威王的上、中、下等马分别记为，，，田忌的上、中、下等马分别记为，，，则他们比赛的情况如下：齐威王的马胜者田忌的马齐威王田忌的马齐威王田忌的马齐威王田忌的马齐威王田忌的马田忌田忌的马齐威王 由上表可知，只有齐威王的马对田忌的马这种情况，田忌获胜，所以田忌获胜的概率．故选：D7．我国古代数学家刘徽在《九章算术注》中提出了割圆术:“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣".这可视为中国古代极限思想的佳作.割圆术可以视为将一个圆内接正n边形等分成n个等腰三角形(如图所示)，当n变得很大时，等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想，可得到sin 的近似值为（    ）A．0.035 B．0.026 C．0.018 D．0.033【答案】A【解析】将一个单位圆分成180个扇形，则每个扇形的圆心角度数均为，由这180个扇形对应的等腰三角形的面积之和近似于单位圆的面积，能求出的近似值．【详解】解：将一个单位圆分成180个扇形，则每个扇形的圆心角度数均为，这180个扇形对应的等腰三角形的面积之和近似于单位圆的面积，，．故选：．8．函数的部分图象大致为（    ）A． B．C． D．【答案】B【分析】根据图象，知函数存在奇偶性，先判断函数的奇偶性，然后根据结合函数值的正负，可得出答案.【详解】函数，定义域为，，所以函数为奇函数，则排除AD项；当时，，，所以有，所以，B项符合条件.故选：B.9．已知函数，则下面结论错误的是（    ）A．当时，的取值范围是B．在上单调递减C．的图像关于直线对称D．的图像可由函数的图像向右平移个单位得到【答案】D【分析】先应用辅助角公式化简，再分别根据值域判断A选项，根据单调性判断B选项，根据对称轴判断C选项，根据平移判断D选项. 【详解】,当,,,的取值范围是,A正确;当,,单调递减,B选项正确;当时, ,的图像关于直线对称,C选项正确;由函数的图像向右平移个单位得到,D选项错误.故选:D10．已知双曲线的右焦点为，以为圆心，实轴长为半径的圆与双曲线的一条渐近线相交于两点，当面积最大时，双曲线的离心率为（   ）A． B． C． D．【答案】B【分析】根据点到直线的距离求出的高，由勾股定理得出，当面积最大时，求出关系式，此时可求离心率.【详解】设双曲线的一条渐近线为，为的中点，可得，右焦点为，所以到渐近线的距离为，实轴长为半径,可知，，根据基本不等式，当且仅当时取到等号，所以面积最大时，此时双曲线的离心率.故选: B.11．定义在 上的函数 满足，则不等式 的解集为（　　）A．  B． C．  D． 【答案】D【分析】构造新函数，利用导数说明其单调性，将变形为，利用函数的单调性即可求解.【详解】令 ，则，由于,故,故在单调递增，而 ，由，得 ，∴ ，即 ,∴不等式的解集为,故选：D．12．如图，四边形为正方形，四边形为矩形，且平面与平面互相垂直.若多面体 的体积为，则该多面体外接球表面积的最小值为A． B． C． D．【答案】B【分析】根据题意，设出正方形边长和矩形的高，根据体积公式，求得等量关系；再找到球心，求得半径，利用导数求函数的最小值，则问题得解.【详解】根据题意，连接交于点，过作//交于点，交于，连接.因为四边形是正方形，故可得，又因为平面平面，且交线为，又平面，故平面，不妨设，故可得多面体的体积；则，解得；又容易知多面体外接球的球心在四边形外心的垂线上，且为的中点，设外接球半径为，则；将代入可得，不妨令，则，则，容易知是关于的单调增函数，且当时，，故可得在上单调递减，在单调递减.故.则外接球表面积的最小值.故选：B.【点睛】本题考查棱锥体积的计算、面面垂直的性质、外接球表面积的计算、利用导数求函数的最值，属压轴题. 二、填空题13．在三棱锥内任取一点P，使得的概率是___________.【答案】【分析】求出时，三棱锥的高，过此时的点作平行于底面的截面，要使，则点在三棱锥中，根据体积之比即可得出答案.【详解】解：设点三棱锥的高为，三棱锥的高为，则，若，则，所以，过此时的点作平行于底面的截面如图所示，则点到平面的距离为，故，要使，则点在三棱锥中，所以使得的概率是.故答案为：.14．设，若，则______．【答案】【分析】结合已知条件，利用指对互化和对数的运算即可求解.【详解】因为，，所以，即，从而，故.故答案为：.15．在锐角中，，，若在上的投影长等于的外接圆半径R，则R=______.【答案】2【分析】根据正弦定理和投影长求出，结合得到，利用正弦定理求出答案.【详解】由题意得，，，即，即，因为，所以，故，故.故答案为：216．已知抛物线，焦点为，准线与x轴的交点为，过点的直线与抛物线交于、两点，且满足，则______.【答案】/【分析】联立直线和抛物线方程，由韦达定理以及弦长公式得出，再由抛物线的定义以及余弦定理得出，进而得出，最后由得出答案.【详解】根据对称性，不妨设由题意知，则可设直线的方程为.由，可得①所以.所以.因为，所以在中，由余弦定理得因此，得，代入①得.解得，因此 故答案为：   三、解答题17．已知等比数列的公比，前项和为．若，且是与的等差中项.(1)求；(2)设数列满足，，数列的前项和为.求．【答案】(1)(2) 【分析】（1）根据题意，利用等比数列的通项公式列出方程求得的值，进而求得数列的通项公式；（2）根据题意，利用，求得，得到，结合等比数列的求和公式，即可求解.【详解】（1）解：由，得，又由是，的等差中项，可得，即，则， 即，可得，解得或，因为，所以，将代入，可得，所以，即.（2）解：因为数列满足，，可得，，所以当时，，又因为也满足上式，所以，则，所以 .18．新能源汽车是指除汽油、柴油发动机之外的所有其他能源汽车，被认为能减少空气污染和缓解能源短缺的压力．在当今提倡全球环保的前提下，新能源汽车越来越受到消费者的青睐，新能源汽车产业也必将成为未来汽车产业发展的导向与目标．某车企统计了近期购车的车主性别与购车种类的情况，其中购车的男性占近期购车车主总人数的60%．现有如下表格： 购置新能源汽车（辆）购置传统燃油汽车（辆）总计男性60女性   总计    (1)若女性购置新能源汽车人数为所有购车总人数的25%，男性购置传统燃油汽车人数为所有购车总人数的10%，试完成上面的列联表，并判断能否有95%的把握认为是否购置新能源汽车与性别有关；(2)若，，在该车企近期统计的男性购车车主中，求购置新能源汽车的人数大于购置传统燃油汽车人数的2倍的概率．参考公式及数据：，其中．0.150.050.0100.0050.0012.0723.8416.6357.87910.828【答案】(1)填表见解析；有95%的把握认为是否购置新能源汽车与性别有关(2) 【分析】（1）由题意补充列联表，计算卡方后判断（2）由古典概型求解【详解】（1）列联表如下： 购置新能源汽车（辆）购置传统燃油汽车（辆）总计男性501060女性251540总计7525100 因为，所以有95%的把握认为是否购置新能源汽车与性别有关．（2）根据题意可知，因为，，所以基本事件分别为，，，，，，，，，，，，，，共14种，设购置新能源汽车的人数大于购置传统燃油汽车人数的2倍为事件，则，满足题意的事件有，，，，，，，，，，共10个，所求的概率．19．如图，在三棱锥中，和均为边长为2的等边三角形．(1)证明：．(2)若与平面所成的角为，求三棱锥的体积．【答案】(1)证明见解析(2) 【分析】（1）取的中点，连接，，证出，，由线面垂直的判定定理和性质定理即可得到证明.（2）由（1）知平面平面，由此可得线面角为，进而求得，的长，然后由棱锥体积公式计算可得答案.【详解】（1）证明：取的中点，连接，．因为和均为等边三角形，所以，．因为，平面，所以平面．又平面，所以．（2）由（1）知平面，又平面，所以平面平面，平面平面，故过作平面的垂线，垂足为，则一定在直线上，因为与平面所成的角为，所以．由题意知，所以，所以，所以．故三棱锥的体积．20．如图，已知椭圆的左、右顶点分别为A，B，点C是椭圆上异于A，B的动点，过原点O平行于AC的直线与椭圆交于点M，N，AC的中点为点D，直线OD与椭圆交于点P，Q，点P，C，M在x轴的上方．  (1)当时，求；(2)求的最大值．【答案】(1)－(2)10 【分析】（1）设，根据题意求得，得到，进而得到，方法1、由直线的方程为，联立方程组，分别求得的坐标，得到向量和，结合向量的夹角公式，即可求解；方法2、由，求得，结合，即可求解；方法3、由，结合，即可求解.（2）设点，得到，设直线的方程为，联立方程组求得，同理得到，方法1、求得，令，利用二次函数的图象与性质，求得，结合，即可求解；方法2、求得，利用基本不等式求得，进而求得的最大值.【详解】（1）解：设，因为，且，可得，又因为，解得或（舍去），因为点在轴上方，则，可得，即点的坐标为，由点为的中点，所以点的坐标为，所以，方法1  由于直线过原点且与直线平行，则直线的方程为，因为点在的上方，可得，由，解得，则，所以，则，由，解得，则，所以，则，则；方法2  由于直线过原点且与直线平行，则，因为，可得，则，因为，所以，可得，则.方法3  由于直线过原点且与直线平行，则，因为，则.（2）解：设点，由，可得，则,可得，又由直线的斜率一定存在且不为零，故可设其方程为，由，解得，则，因为，可得，同理可得，方法1  由题可得，令，则，可得，当时，即时，取等号，即又因为，所以的最大值为.方法2  由题可知，所以，当且仅当时，等号成立，又因为，所以的最大值为.  【点睛】方法技巧：圆锥曲线中的最值问题是高考中的热点问题，常涉及不等式、函数的值域问题，综合性比较强，解法灵活多样，但主要有两种方法：（1）几何转化代数法：若题目的条件和结论能明显体现几何特征和意义，则考虑利用圆锥曲线的定义、图形、几何性质来解决；（2）函数取值法：若题目的条件和结论的几何特征不明显，则可以建立目标函数，再求这个函数的最值（或值域），常用方法：（1）配方法；（2）基本不等式法；（3）单调性法；（4）三角换元法；（5）平面向量；（6）导数法等，要特别注意自变量的取值范围.21．已知，，(1)若与在处的切线重合，分别求，的值.(2)若，恒成立，求的取值范围.【答案】(1)，(2) 【分析】（1）求出函数的导函数，依题意可得且，即可得到方程组，解得即可；（2）依题意可得对恒成立，令，求出函数的导函数，由可得，从而求出的值，再验证即可.【详解】（1）解：因为，，所以.，，因为且，即且，解得，.（2）解：因为对恒成立，.对恒成立，即对恒成立，令，因为，所以是的最小值点，且是的极值点，即，因为在上单调递增，且，所以，下面检验：当时，对恒成立，因为，所以当时，当时，所以在上单调递减，在上单调递增.所以，符合题意，所以.22．在直角坐标系中，圆的参数方程为(参数)，以为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为.（1）求的极坐标方程；（2）若射线与圆的交点为，与直线的交点为，求的取值范围.【答案】（1）；（2）.【详解】试题分析：（1）圆C的参数方程消去参数φ，能求出圆C的普通方程，再由x=ρcosθ，y=ρsinθ，能求出圆C的极坐标方程．（2）设P（ρ1，θ1），则有ρ1=cosθ1，Q（ρ2，θ1），则，=ρ1ρ2，结合tanθ1＞0，能求出的范围．试题解析：（1）圆的普通方程是，又，所以圆的极坐标方程是.    （2）设，则有 ，设，且直线的方程是，则有所以因为，所以.23．已知函数f（x）＝2|x＋1|＋|x－3|．(1)求不等式f（x）>10的解集；(2)若函数的最小值为M，正数a，b，c满足a＋b＋c＝M，证明．【答案】(1)(2)证明见解析 【分析】（1）分段讨论去绝对值即可求解；（2）利用绝对值不等式可求得，再利用基本不等式即可证明.【详解】（1）当时，由，解得，此时；当时，由，解得，此时；当时，由，解得，此时．综上所述，不等式的解集为．（2）证明：因为，所以M＝8，所以a＋b＋c＝8．因为，，，当且仅当时，等号成立，所以，故．