备战2024高考一轮复习数学（理） 第二章 函数的概念及基本初等函数(Ⅰ) 第九节 函数模型及其应用课件PPT

这是一份备战2024高考一轮复习数学（理） 第二章 函数的概念及基本初等函数(Ⅰ) 第九节 函数模型及其应用课件PPT，共38页。PPT课件主要包含了答案B等内容，欢迎下载使用。
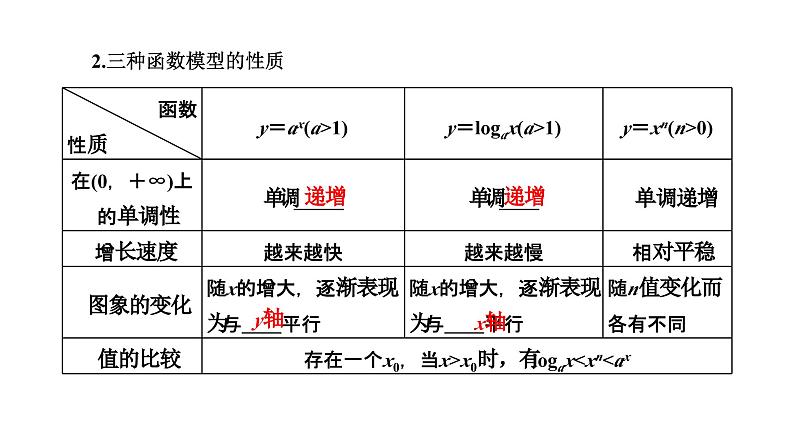
2.三种函数模型的性质
(1)“直线上升”是匀速增长，其增长量固定不变；“指数增长”先慢后快，其增长量成倍增加，常用“指数爆炸”来形容；“对数增长”先快后慢，其增长速度缓慢．(2)充分理解题意，并熟练掌握几种常见函数的图象和性质是解题的关键．(3)易忽视实际问题中自变量的取值范围，需合理确定函数的定义域，必须验证数学结果对实际问题的合理性．
1．已知甲、乙两种商品在过去一段时间内的价格走势如图所示．假设某商人持有资金120万元，他可以在t1至t4的任意时刻买卖这两种商品，且买卖能够立即成交(其他费用忽略不计)．如果他在t4时刻卖出所有商品，那么他将获得的最大利润是(　 )A．40万元 B．60万元 C．80万元 D．120万元解析：当甲商品的价格为6元时，该商人全部买入甲商品，可以买120÷6＝20(万份)，在t2时刻全部卖出，此时获利20×2＝40(万元)；当乙商品的价格为4元时，该商人买入乙商品，可以买(120＋40)÷4＝40(万份)，在t4时刻全部卖出，此时获利40×2＝80(万元)．故该商人共获利40＋80＝120(万元)．答案：D　
3．已知f(x)＝x2，g(x)＝2x，h(x)＝lg2x，当x∈(4，＋∞)时，对三个函数的增长速度进行比较，下列选项中正确的是(　 )A．f(x)>g(x)>h(x) B．g(x)>f(x)>h(x)C．g(x)>h(x)>f(x) D．f(x)>h(x)>g(x)解析：在同一平面直角坐标系内，根据函数图象变化趋势，当x∈(4，＋∞)时，增长速度由大到小依次g(x)>f(x)>h(x)．答案：B　
2．某小型服装厂生产一种风衣，日销售量x(单位：件)与单价P(单位：元)之间的关系为P＝160－2x，生产x件所需成本为C(单位：元)，其中C＝500＋30x，若要求每天获利不少于1 300元，则日销量x的取值范围是(　 )A．{x|20≤x≤30，x∈N*} B．{x|20≤x≤45，x∈N*}C．{x|15≤x≤30，x∈N*} D．{x|15≤x≤45，x∈N*}解析：由题意日销量x件时，利润是y＝(160－2x)x－(500＋30x)＝－2x2＋130x－500，－2x2＋130x－500≥1 300，(x－20)(x－45)≤0,20≤x≤45.故选B.答案：B　
[一“点”就过]求解已知函数模型解决实际问题的关键(1)认清所给函数模型，弄清哪些量为待定系数．(2)根据已知利用待定系数法，确定模型中的待定系数．(3)利用该函数模型，借助函数的性质、导数等求解实际问题，并进行检验.
基础点(二)　利用函数图象刻画实际问题　[题点全训]1．(2022·肇庆高三三模)某工厂从2013年开始，近八年以来生产某种产品的情况是：前四年年产量的增长速度越来越慢，后四年年产量的增长速度保持不变，则该厂这种产品的年产量y与时间t的函数图象可能是(　 )解析：由题意可得，图象的几何特征应为从左向右看每个点的切线斜率应逐渐减小，然后斜率变为一个固定的值，符合此特征的只有选项B中的图象，故选B.
2．已知正方形ABCD的边长为4，动点P从点B开始沿折线BCDA向A点运动．设点P运动的路程为x，△ABP的面积为S，则函数S＝f(x)的图象是(　 )解析：依题意知，当0≤x≤4时，f(x)＝2x；当4