




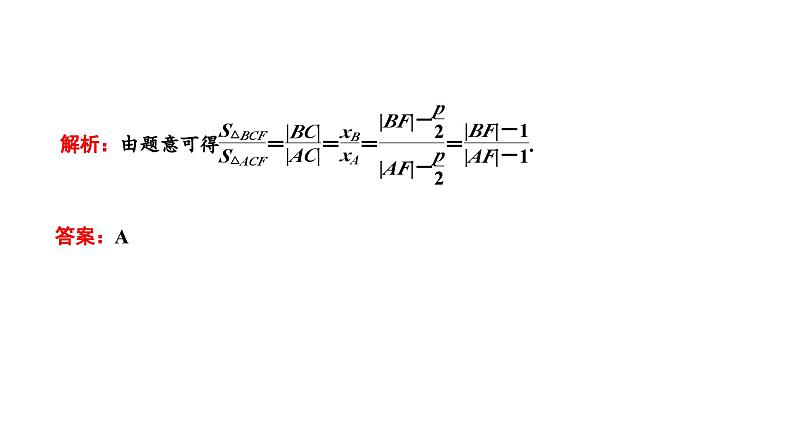


备战2024高考一轮复习数学(理) 第九章 解析几何 习题课4——“解析几何”问题常用的解题技能课件PPT
展开
这是一份备战2024高考一轮复习数学(理) 第九章 解析几何 习题课4——“解析几何”问题常用的解题技能课件PPT,共56页。PPT课件主要包含了答案D等内容,欢迎下载使用。
[反思领悟]本题巧妙运用椭圆和双曲线的定义建立|AF1|,|AF2|的等量关系,从而快速求出双曲线实半轴长a的值,进而求出双曲线的离心率,大大降低了运算量.
方法(二) 设而不求,金蝉脱壳设而不求是解析几何解题的基本手段,是比较特殊的一种思想方法,其实质是整体结构意义上的变式和整体思想的应用.设而不求的灵魂是通过科学的手段使运算量最大限度地减少,通过设出相应的参数,利用题设条件加以巧妙转化,以参数为过渡,设而不求.
[反思领悟](1)本题设出A,B两点的坐标,却不求出A,B两点的坐标,巧妙地表达出直线AB的斜率,通过将直线AB的斜率“算两次”建立几何量之间的关系,从而快速解决问题.(2)在运用圆锥曲线问题中的设而不求方法技巧时,需要做到:①凡是不必直接计算就能更简洁地解决问题的,都尽可能实施“设而不求”;②“设而不求”不可避免地要设参、消参,而设参的原则是宜少不宜多.
[反思领悟]要求△APF的周长的最小值,其实就是转化为求解三角形三边长之和,根据已知条件与双曲线定义加以转化为已知边的长度问题与已知量的等价条件来分析,根据直线与双曲线的位置关系,通过数形结合确定点P的位置,通过求解点P的坐标进而利用三角形的面积公式来处理.
方法(四) 妙借向量,无中生有平面向量是衔接代数与几何的纽带,沟通“数”与“形”,融数、形于一体,是数形结合的典范,具有几何形式与代数形式的双重身份,是数学知识的一个交汇点和联系多项知识的媒介.妙借向量,可以有效提升圆锥曲线的解题方向与运算效率,达到良好效果.
[反思领悟]本题通过相关向量坐标的确定,结合∠BFC=90°,巧妙借助平面向量的坐标运算来转化圆锥曲线中的相关问题,从形入手转化为相应数的形式,简化运算.
[反思领悟]1.四边形或多个图形面积的关系的转化分析图形的底和高中是否存在“同底”或“等高”的特点(尤其是有平行条件的时候),可将面积的关系转化,降低计算量.特殊地,对角线互相垂直的四边形,面积=对角线长度乘积的一半.2.面积的最值或取值范围问题一般都是利用面积公式表示面积,然后将面积转化为某个变量的一个函数,再求解函数的最值(一般处理方法有换元,基本不等式,建立函数模型,利用二次函数、三角函数的有界性求最值或利用导数法求最值,构造函数求导等等),在算面积的过程中,优先选择长度为定值的线段参与运算,灵活使用割补法计算面积,尽可能降低计算量.
[反思领悟]解题过程中要善于发现“同构”形式,在解题中清晰展示“同构”,进而以“同理可得”简化运算.
相关课件
这是一份备战2024高考一轮复习数学(理) 第三章 导数及其应用 习题课1——“函数与导数”问题常用的解题技能课件PPT,共34页。
这是一份备战2024高考一轮复习数学(理) 第九章 解析几何 习题课3——圆锥曲线中的证明、存在性问题课件PPT,共17页。
这是一份备战2024高考一轮复习数学(理) 第九章 解析几何 习题课2——圆锥曲线中的定点、定值问题课件PPT,共18页。









