备战2024高考一轮复习数学（理） 第七章 不等式、推理与证明、程序框图 第四节 合情推理与演绎推理课件PPT

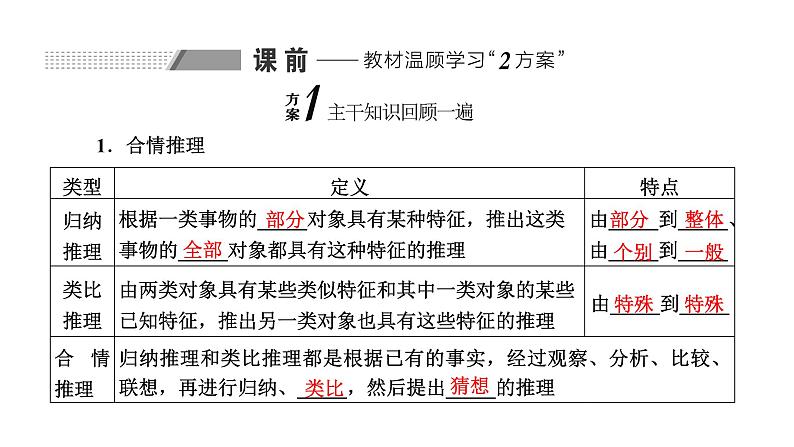
这是一份备战2024高考一轮复习数学（理） 第七章 不等式、推理与证明、程序框图 第四节 合情推理与演绎推理课件PPT，共42页。PPT课件主要包含了合情推理，答案C，答案A等内容，欢迎下载使用。
2．演绎推理(1)定义：从一般性的原理出发，推出某个特殊情况下的结论，我们把这种推理称为演绎推理．简言之，演绎推理是由一般到_____的推理．(2)“三段论”是演绎推理的一般模式，包括：①大前提——已知的一般原理；②小前提——所研究的特殊情况；③结论——根据一般原理，对特殊情况做出的判断．
(1)合情推理包括归纳推理和类比推理，其结论是猜想，不一定正确，若要确定其正确性，则需要证明．(2)在进行类比推理时，要从本质上去类比，只从一点表面现象去类比，就会犯机械类比的错误．(3)应用三段论解决问题时，要明确什么是大前提、小前提，如果前提与推理形式是正确的，结论必定是正确的．若大前提或小前提错误，尽管推理形式是正确的，但所得结论是错误的．
[一“点”就过] 破解归纳推理的思维步骤
3．过正三角形的外接圆的圆心且平行于一边的直线分正三角形两部分的面积比为4∶5，类比此性质：过正四面体的外接球的球心且平行于一个面的平面分正四面体两部分的体积比为________．解析：在平面内，过正三角形外接圆圆心平行于一边的直线截得高的长度比为2∶1，所以分正三角形两部分面积比为22∶[(2＋1)2－22]＝4∶5，所以在空间内，过正四面体外接球球心且平行于一个平面截得高的长度比为3∶1，所以分正四面体两部分体积比为33∶[(3＋1)3－33]＝27∶37.答案：27∶37
[一“点”就过] 类比推理应用的类型及解题策略
[解析]　(1)若甲预测正确，则乙、丙预测错误，即①甲的成绩比乙高；②丙的成绩不是最高的；③丙的成绩比乙低．由①②③可得甲、乙、丙成绩由高到低的顺序为甲、乙、丙，A正确．(2)若乙预测正确，则甲、丙预测错误，即①乙的成绩比甲高；②丙的成绩最高；③丙的成绩比乙低．由上可知②③相矛盾，故此情况不成立．(3)若丙预测正确，则甲、乙预测错误，即①乙的成绩比甲高；②丙的成绩不是最高的；③丙的成绩比乙高．由①③得成绩由高到低的顺序为丙、乙、甲，与②相矛盾，此情况不成立．故选A.[答案]　A
[方法技巧](1)演绎推理是从一般到特殊的推理，其一般形式是三段论，应用三段论解决问题时，应当首先明确什么是大前提和小前提，如果大前提是显然的，则可以省略；(2)在推理论证过程中，一些稍复杂一点的证明题常常要由几个三段论才能完成．　　
解析：若甲未获奖，则乙、丙、丁三位同学获奖，此时甲、乙、丙说的都错了，与题设矛盾，所以甲一定获奖了；若丙未获奖，则甲、乙、丁三位同学获奖，此时甲、丙、丁说的都对，与题设矛盾，所以丙也一定获奖了，由此可知乙、丁只有一个获奖，不可能同时获奖，故选C.答案：C　
解析：由题得：这个数列各项的值分别为1,1,3,1,5,3,7,1,9,5,11,3，…所以a24＋a25＝3＋25＝28.又因为a5＝5，a10＝5，a20＝5，a40＝5，…，即项的值为5时，下角码是首项为5，公比为2的等比数列．所以第8个5是该数列的第5×28－1＝640项．答案：28　640
2．(体现数学应用)我们在求高次方程或超越方程的近似解时常用二分法求解，在实际生活中还有三分法．比如借助天平鉴别假币，有三枚形状大小完全相同的硬币，其中有一假币(质量较轻)，把两枚硬币放在天平的两端，若天平平衡，则剩余一枚为假币，若天平不平衡，较轻的一端放的硬币为假币．现有27枚这样的硬币，其中有一枚是假币(质量较轻)，如果只有一台天平，那么一定能找到这枚假币所需要使用天平的最少次数为(　 )A．2 B．3 C．4 D．5
解析：第一步，将27枚硬币分为三组，每组9枚，任取两组分别放于天平左右两端，若天平平衡，则假币在第三组中；若天平不平衡，假币在较轻的那一组中．第二步，把较轻的9枚硬币再分成三组，每组3枚，任取两组分别放于天平左右两端，若天平平衡，则假币在第三组；若天平不平衡，则假币在较轻的一组．第三步，再将假币所在的一组分成三组，每组1枚，任取其中两组放于天平左右两端，若天平平衡，则假币是剩下的一枚；若天平不平衡，则较轻的盘中所放的为假币．因此，一定能找到假币最少需使用3次天平．故选B.答案：B　
解析：当a>1时，y＝ax为增函数；当0