备战2024高考一轮复习数学（理） 第七章 不等式、推理与证明、程序框图 第五节 直接证明与间接证明、数学归纳法课件PPT

这是一份备战2024高考一轮复习数学（理） 第七章 不等式、推理与证明、程序框图 第五节 直接证明与间接证明、数学归纳法课件PPT，共35页。PPT课件主要包含了推理论证，证明的结论，充分条件，不成立，原命题成立，n＝k＋1，答案等边三角形等内容，欢迎下载使用。
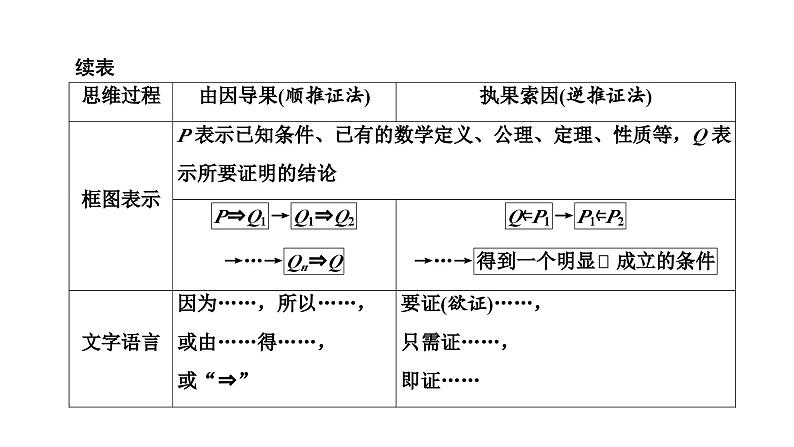
1．直接证明——综合法、分析法
2．间接证明间接证明是不同于直接证明的又一类证明方法，反证法是一种常用的间接证明方法．(1)反证法的定义：假设原命题_______ (即在原命题的条件下，结论不成立)，经过正确的推理，最后得出矛盾，因此说明假设错误，从而证明了____________的证明方法．(2)用反证法证明的一般步骤：①反设——假设命题的结论不成立；②归谬——根据假设进行推理，直到推出矛盾为止；③结论——断言假设不成立，从而肯定原命题的结论成立．
从n0开始的所有正整数n
(1)分析法是执果索因，实际上是寻找使结论成立的充分条件；综合法是由因导果，就是寻找已知的必要条件．(2)综合法和分析法都是直接证明的方法，反证法是间接证明的方法．(3)用反证法证题时，首先否定结论，否定结论就是找出结论的反面的情况，然后推出矛盾，矛盾可以与已知、公理、定理、事实或者假设等相矛盾．(4)推证n＝k＋1时，一定要用上n＝k时的假设，否则就不是数学归纳法．
解析：根据反证法的定义，假设是对原命题结论的否定，故假设三个内角都大于60°.答案：B　
[一“点”就过]综合法的证题思路(1)综合法是“由因导果”的证明方法，它是一种从已知到未知(从题设到结论)的逻辑推理方法，即从题设中的已知条件或已证的真实判断(命题)出发，经过一系列中间推理，最后导出所要求证结论的真实性．(2)综合法的逻辑依据是三段论式的演绎推理．
[一“点”就过]分析法的证题思路先从结论入手，由此逐步推出保证此结论成立的充分条件，而当这些判断恰恰都是已证的命题(定义、公理、定理、法则、公式等)或要证命题的已知条件时命题得证．
[方法技巧]用反证法证明命题的基本步骤(1)反设，设要证明的结论的反面成立．(2)归谬，从反设入手，通过推理得出与已知条件或公理、定理矛盾．(3)否定反设，得出原命题结论成立．　　
[方法技巧]1．应用数学归纳法时需注意以下几点：(1)明确初始值n0并验证当n＝n0时式子成立．(2)由n＝k证明n＝k＋1时，弄清左边增加的项，且明确变形目标．(3)掌握恒等变形常用的方法：①因式分解；②添拆项；③配方法．2．用数学归纳法证明与n有关的不等式，在归纳假设使用后可运用比较法、综合法、分析法、放缩法等来加以证明，充分应用基本不等式、不等式的性质等放缩技巧，使问题得以简化．　　
[方法技巧](1)利用数学归纳法可以探索与正整数n有关的未知问题、存在性问题，其基本模式是“归纳—猜想—证明”，即先由合情推理发现结论，然后经逻辑推理论证结论的正确性．(2)“归纳—猜想—证明”的基本步骤是“试验—归纳—猜想—证明”．高中阶段与数列结合的问题是最常见的问题．　　
“课时验收评价” 见“课时验收评价” （四十三） (单击进入电子文档)