





备战2024高考一轮复习数学(理) 第三章 导数及其应用 第一节 导数的概念及运算、定积分课件PPT
展开
这是一份备战2024高考一轮复习数学(理) 第三章 导数及其应用 第一节 导数的概念及运算、定积分课件PPT,共46页。
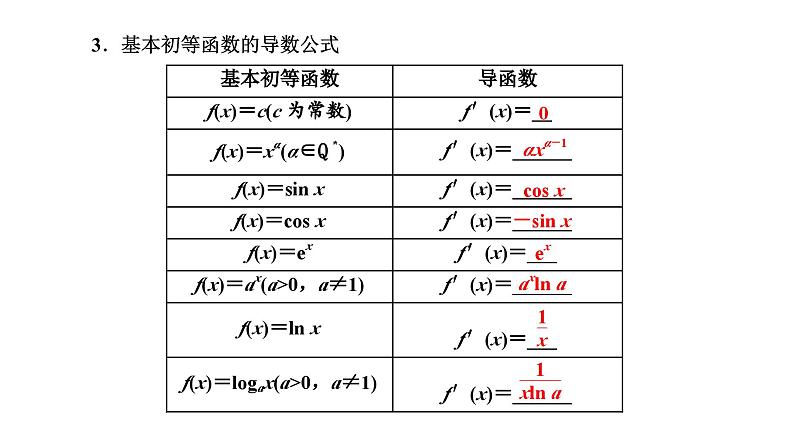
3.基本初等函数的导数公式
(1)f′(x0)代表函数f(x)在x=x0处的导数值;(f(x0))′是函数值f(x0)的导数,且(f(x0))′=0.(2)奇函数的导数是偶函数,偶函数的导数是奇函数.周期函数的导数还是周期函数.(4)曲线的切线与曲线的公共点的个数不一定只有一个,而直线与二次曲线相切只有一个公共点.(5)函数y=f(x)的导数f′(x)反映了函数f(x)的瞬时变化趋势,其正负号反映了变化的方向,其大小|f′(x)|反映了变化的快慢,|f′(x)|越大,曲线在这点处的切线越“陡峭”.(6)在复合函数求导中要分清每一步求导是哪个变量对哪个变量的求导,不能混淆.
1.下列函数中满足f(x)=f′(x)的是( )A.f(x)=3+x B.f(x)=-xC.f(x)=ln x D.f(x)=0解析:若f(x)=0,则f′(x)=0,从而有f(x)=f′(x).故选D.答案:D
答案:D5.曲线y=(ax+1)ex在点(0,1)处的切线的斜率为-2,则a=________.解析:∵y′=(ax+a+1)ex,∴当x=0时,y′=a+1,∴a+1=-2,解得a=-3.答案:-3
2.已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+ln x,则f′(1)=( )A.-e B.-1 C.1 D.e
解:(1)y′=(cs x)′-(sin x)′=-sin x-cs x.(2)∵y=(x+1)(x+2)(x+3)=(x2+3x+2)(x+3)=x3+6x2+11x+6,∴y′=3x2+12x+11.
[一“点”就过](1)求导之前,应利用代数运算、三角恒等式等对函数进行化简,然后求导,尽量避免不必要的商的求导,这样可以减少运算量,提高运算速度,减少差错.(2)①若函数为根式形式,可先化为分数指数幂,再求导.②复合函数求导,应由外到内逐层求导,必要时可进行换元.
基础点(二) 求曲线在某点处的切线方程 [题点全训]1.曲线y=ex-1+x2在x=1处的切线方程为( )A.y=2x+1 B.y=2xC.y=3x-1 D.y=3x解析:对函数y=ex-1+x2求导得y′=ex-1+2x,故当x=1时,斜率k=e1-1+2=3,又切线过点(1,2),故切线方程为y-2=3(x-1),即y=3x-1.答案:C
[一“点”就过]正确选用求定积分的4个常用方法
层级二/ 重难点——逐一精研(补欠缺)重难点(一) 求曲线过某点的切线方程 [典例] 若经过点P(2,8)作曲线y=x3的切线,则切线方程为( )A.12x-y-16=0B.3x-y+2=0C.12x-y+16=0或3x-y-2=0D.12x-y-16=0或3x-y+2=0
过点的切线方程的求解方法设切点为P(x0,y0),则斜率k=f′(x0),过切点的切线方程为y-y0=f′(x0)(x-x0),又因为切线方程过点A(m,n),所以n-y0=f′(x0)(m-x0),然后解出x0的值.(x0有几个值,就有几条切线)[提醒] 在做此类题目时要分清题目提供的点在曲线上还是在曲线外.
重难点(二) 求切点坐标或参数 [典例] (1)已知曲线y=2ex-1在x0处的切线方程为2ex-y+m=0,则( )A.m=-1 B.m=-1-eC.m=1 D.m=e(2)函数f(x)=ln x+ax的图象上存在与直线2x-y=0平行的切线,则实数a的取值范围是________.[解析] (1)因为y=2ex-1,所以y′=2ex,所以曲线y=2ex-1在x0处的切线的斜率为k=y′|x=x0=2ex0,又因为切线方程为2ex-y+m=0,即y=2ex+m,得k=2e,
所以2ex0=2e,解得x0=1,所以当x=x0=1时,y=2ex0-1=2e-1,即切点为(1,2e-1),将其代入切线方程得2e×1-(2e-1)+m=0,得m=-1.
求切点、参数问题的方法通常根据曲线、切线、切点的三个关系列出关于参数的方程(组)并解出参数,注意以下几点:切点处的导数是切线的斜率;切点在切线上;切点在曲线上.
2.曲线y=sin x+2x+1在点P处的切线方程是3x-y+1=0,则切点P的坐标是________.解析:由函数y=sin x+2x+1,则y′=cs x+2,设切点P的坐标为(x0,y0),则斜率k=y′|x=x0=cs x0+2=3,所以cs x0=1,解得x0=2kπ(k∈Z),当k=0时,切点为(0,1),此时切线方程为3x-y+1=0;当k≠0,切点为(2kπ,4kπ+1)(k∈Z),不满足题意.综上可得,切点为(0,1).答案:(0,1)
重难点(三) 公切线问题 [典例] 已知函数f(x)=x2-2m,g(x)=3ln x-x,若y=f(x)与y=g(x)在公共点处的切线相同,则m=( )A.-3 B.1 C.2 D.5
确定两曲线的公切线问题,切点是切线的核心,解决这类问题的关键是设出切点的坐标,用好相切的特征,即若两个函数的图象有相同的切线,则需根据函数与切线在切点处的函数值相等以及两函数在切点处的导函数的函数值也相等,构建方程(组)加以求解.
层级三/ 细微点——优化完善(扫盲点)1.(忽略f′(x)的意义)如图所示为函数y=f(x),y=g(x)的导函数的图象,那么y=f(x),y=g(x)的图象可能是( )解析:由y=f′(x)的图象知,y=f′(x)在(0,+∞)上单调递减,说明函数y=f(x)的切线的斜率在(0,+∞)上也单调递减,故可排除A、C.又由图象知y=f′(x)与y=g′(x)的图象在x=x0处相交,说明y=f(x)与y=g(x)的图象在x=x0处的切线的斜率相同,故可排除B.故选D.答案:D
3.(不理解瞬时变化率的意义)已知曲线f(x)=2x2+1在点M(x0,f(x0))处的瞬时变化率为-8,则点M的坐标为________.解析:∵f(x)=2x2+1,∴f′(x)=4x,令4x0=-8,则x0=-2,∴f(x0)=9,∴点M的坐标是(-2,9).答案:(-2,9)
4.(借助数学文化)我国魏晋时期的科学家刘徽创立了“割圆术”,实施“以直代曲”的近似计算,用正n边形进行“内外夹逼”的办法求出了圆周率π的精度较高的近似值,这是我国最优秀的传统科学文化之一.借用“以直代曲”的近似计算方法,在切点附近,可以用函数图象的切线近似代替在切点附近的曲线来近似计算.设f(x)=ex2,则f′(x)=________,其在点(0,1)处的切线方程为________.解析:∵f(x)=ex2,故f′(x)=(x2)′e x2=2xex2,则f′(0)=0.故曲线y=f(x)在点(0,1)处的切线方程为y=1.答案:2xex2 y=1
6.(强化开放思维)请写出与曲线f(x)=x3+1在点(0,1)处具有相同切线的一个函数(非常数函数)的解析式为g(x)=____________.解析:f′(x)=3x2,f′(0)=0,曲线f(x)=x3+1在点(0,1)处的切线方程为y=1,所有在点(0,1)处的切线方程为y=1的函数都是正确答案.答案:x2+1或-x2+1或cs x等(答案不唯一)
“课时验收评价”见“课时验收评价(十四)” (单击进入电子文档)
相关课件
这是一份2024版新教材高考数学全程一轮总复习第三章导数及其应用第一节导数的概念及其意义导数的运算课件,共44页。PPT课件主要包含了必备知识·夯实双基,关键能力·题型突破,f′x0,切线的斜率,nxn-1,cosx,-sinx,axlna,cf′x,答案C等内容,欢迎下载使用。
这是一份备战2024年高考总复习一轮(数学)第3章 导数及其应用 第1节 导数的概念及运算课件PPT,共34页。PPT课件主要包含了内容索引,强基础固本增分,研考点精准突破,xx0,提示不一定,考向1求切线的方程,答案D等内容,欢迎下载使用。
这是一份2024版高考数学一轮复习教材基础练第三章导数及其应用第一节导数的概念及其意义导数的运算教学课件,共32页。PPT课件主要包含了教材知识萃取,导数的运算,方法技巧,导数运算的技巧,教材素材变式,求切线方程的方法,方法总结等内容,欢迎下载使用。