备战2024高考一轮复习数学（理） 第一章 集合与常用逻辑用语 第三节 简单的逻辑联结词、全称量词与存在量词课件PPT

这是一份备战2024高考一轮复习数学（理） 第一章 集合与常用逻辑用语 第三节 简单的逻辑联结词、全称量词与存在量词课件PPT，共28页。PPT课件主要包含了∀x∈M綈px等内容，欢迎下载使用。

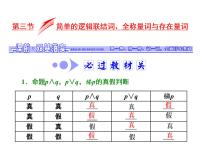
1．简单的逻辑联结词(1)命题中的且、或、非叫做逻辑联结词．(2)命题p∧q、p∨q、綈p的真假判断
(3)含有逻辑联结词的命题真假判断口诀①p∨q→见真即真，p∧q→见假即假，p与綈p→真假相反．②“p∨q”的否定是“(綈p)∧(綈q)”，“p∧q”的否定是“(綈p)∨(綈q)”．
2．全称量词和存在量词
3．全称(特称)命题及含一个量词的命题的否定
∃x0∈M，綈p(x0)
1．逻辑联结词“或”“且”“非”对应集合运算中的“并”“交”“补”，可借助集合运算处理含逻辑联结词的命题．2．含有一个量词命题的否定规律是“改变量词，否定结论”．3．命题p与p的否定的真假性相反．
1．命题“方程x2－1＝0的解是x＝±1”中使用逻辑联结词的情况是(　 )A．没有使用逻辑联结词 B．使用了逻辑联结词“或”C．使用了逻辑联结词“且” D．使用了逻辑联结词“非”答案：B　2．若命题“p∧q”为假，且“綈p”为假，则(　 )A．“p∨q”为假 B．q假C．q真 D．不能判断q的真假答案：B
3．命题“∃x<0，使x2－3x＋1≥0”的否定是(　 )A．∃x<0，使x2－3x＋1<0B．∃x≥0，使x2－3x＋1<0C．∀x<0，使x2－3x＋1<0D．∀x≥0，使x2－3x＋1<0答案：C4．下列命题中的假命题是(　 )A．∃x0∈R，lg x0＝1 B．∃x0∈R，sin x0＝0C．∀x∈R，x3>0 D．∀x∈R,2x>0解析：当x0＝10时，lg x0＝1，故A是真命题；当x0＝0时，sin x0＝0，故B是真命题；当x＝－1时，x3<0，故C是假命题；由指数函数的值域知D是真命题．答案：C　
2．已知命题p：∃x∈R，cs x>1，则(　 )A．綈p：∃x∈R，cs x≤1B．綈p：∀x∈R，cs x≤1C．綈p：∃x∈R，cs x<1D．綈p：∀x∈R，cs x<1解析：根据含有一个量词的否定，可知命题p：∃x∈R，cs x>1的否定是綈p：∀x∈R，cs x≤1.答案：B　3．已知命题p：∃x0∈R，lg2(3x0＋1)≤0，则(　 )A．p是假命题；綈p：∀x∈R，lg2(3x＋1)≤0B．p是假命题；綈p：∀x∈R，lg2(3x＋1)>0C．p是真命题；綈p：∀x∈R，lg2(3x＋1)≤0D．p是真命题；綈p：∀x∈R，lg2(3x＋1)>0解析：∵3x>0，∴3x＋1>1，则lg2(3x＋1)>0，∴p是假命题，綈p：∀x∈R，lg2(3x＋1)>0.故选B.答案：B　
[一“点”就过]1．全称命题与特称命题真假判断的方法要判断全称命题“∀x∈M，p(x)”是真命题，需要对集合M中的每一个元素x，证明p(x)成立；要判断特称命题是真命题，只要在限定集合内找到一个x＝x0，使p(x0)成立即可．2．全称命题与特称命题的进行否定的步骤
层级二/ 重难点——逐一精研(补欠缺)重难点(一)　含有逻辑联结词的命题及其真假判断[典例]　(1)已知命题p：∀x>0，ln(x＋1)>0；命题q：若a>b，则a2>b2.下列命题为真命题的是(　 )A．p∧q　　　　　　　B．p∧(綈q)C．(綈p)∧q D．(綈p)∧(綈q)
A．p∧(綈q) B．(綈p)∧qC．p∧q D．(綈p)∨q
[解析]　(1)当x>0时，x＋1>1，因此ln(x＋1)>0，即p为真命题；取a＝1，b＝－2，这时满足a>b，显然a2>b2不成立，因此q为假命题．由复合命题的真假性，知B为真命题．
[方法技巧]　判断含有逻辑联结词命题真假的步骤
[针对训练]1．(2023·惠州调研)已知命题p，q，则“綈p为假命题”是“p∧q是真命题”的(　 )A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件解析：充分性：若綈p为假命题，则p为真命题，由于不知道q的真假性，所以推不出p∧q是真命题．必要性：p∧q是真命题，则p，q均为真命题，则綈p为假命题．所以“綈p为假命题”是“p∧q是真命题”的必要不充分条件．答案：B　
2．已知命题p：“若x2－x>0，则x>1”；命题q：“若x，y∈R，x2＋y2＝0，则xy＝0”．下列命题是真命题的是(　 )A．p∨(綈q) B．p∨qC．p∧q D．(綈p)∧(綈q)解析：若x2－x>0，则x>1或x<0，故p是假命题；若x，y∈R，x2＋y2＝0，则x＝0，y＝0，xy＝0，故q是真命题．则p∨q是真命题．答案：B　
根据命题的真假求参数范围的步骤(1)求出当命题p，q为真命题时所含参数的取值范围；(2)根据复合命题的真假判断命题p，q的真假性；(3)根据命题p，q的真假情况，利用集合的交集和补集的运算，求解参数的取值范围．　　
[针对训练]1．(变条件)若本例将条件“p或q为假命题”变为“p且q为真命题”，其他条件不变，则实数m的取值范围为________．
2．(变条件)若本例将条件“p或q为假命题”变为“p且q为假，p或q为真”，其他条件不变，则实数m的取值范围为________．
层级三/ 细微点——优化完善(扫盲点)1．(不对命题完全否定致误)已知命题p：∃x≥0，ex<1且sin x>1，则綈p为(　 )A．∃x<0，ex<1且sin x>1B．∃x<0，ex≥1或sin x≤1C．∃x≥0，ex<1或sin x>1D．∀x≥0，ex≥1或sin x≤1解析：命题p：∃x≥0，ex<1且sin x>1，为特称命题，所以綈p：∀x≥0，ex≥1或sin x≤1，故选D.答案：D　
2．(链接生活实际)短道速滑队6名队员(含赛前系列赛积分最靠前的甲乙丙三名队员在内)进行短道速滑赛选拔，记“甲得第一名”为p，“乙得第二名”为q，“丙得第三名”为r，若p∨q是真命题，p∧q是假命题，(綈q)∧r是真命题，则选拔赛的结果为(　 )A．甲得第一名，乙得第二名，丙得第三名B．甲得第二名，乙得第一名，丙得第三名C．甲得第一名，乙得第三名，丙得第二名D．甲得第一名，乙没得第二名，丙得第三名解析：若p∨q是真命题，p∧q是假命题，则p和q一真一假；若(綈q)∧r是真命题，则q是假命题，r是真命题；综上可知，p真q假r真，故“甲得第一名、乙没得第二名、丙得第三名”．故选D.答案：D　
A．p∧q B．p∨(綈q)C．(綈p)∨q D．(綈p)∧(綈q)
4．(混淆否命题与命题的否定)命题“所有奇数的立方都是奇数”的否定是______________________．答案：存在一个奇数，它的立方不是奇数
“课时验收评价”见“课时验收评价(三)” (单击进入电子文档)