【暑假提升】北师大版数学八年级（八升九）暑假-专题第02讲《矩形的性质与判定》预习讲学案

这是一份【暑假提升】北师大版数学八年级（八升九）暑假-专题第02讲《矩形的性质与判定》预习讲学案，文件包含暑假提升北师大版数学八年级八升九暑假-专题第02讲《矩形的性质与判定》预习讲学案解析版docx、暑假提升北师大版数学八年级八升九暑假-专题第02讲《矩形的性质与判定》预习讲学案原卷版docx等2份学案配套教学资源，其中学案共35页， 欢迎下载使用。

第02讲 矩形的性质与判定
【学习目标】
1．理解矩形的概念，知道它们之间的关系以及它们与平行四边形的关系；
2．掌握矩形的性质与判定并能运用这些性质与判定进行有关的证明和计算．
【基础知识】
一．矩形的判定
（1）矩形的判定：
①矩形的定义：有一个角是直角的平行四边形是矩形；
②有三个角是直角的四边形是矩形；
③对角线相等的平行四边形是矩形（或“对角线互相平分且相等的四边形是矩形”）
（2）①证明一个四边形是矩形，若题设条件与这个四边形的对角线有关，通常证这个四边形的对角线相等．
②题设中出现多个直角或垂直时，常采用“三个角是直角的四边形是矩形”来判定矩形．
二．直角三角形斜边上的中线
（1）性质：在直角三角形中，斜边上的中线等于斜边的一半．（即直角三角形的外心位于斜边的中点）
（2）定理：一个三角形，如果一边上的中线等于这条边的一半，那么这个三角形是以这条边为斜边的直角三角形．
该定理可以用来判定直角三角形．
三．矩形的性质
（1）矩形的定义：有一个角是直角的平行四边形是矩形．
（2）矩形的性质
①平行四边形的性质矩形都具有；
②角：矩形的四个角都是直角；
③边：邻边垂直；
④对角线：矩形的对角线相等；
⑤矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点．
（3）由矩形的性质，可以得到直角三角形的一个重要性质，直角三角形斜边上的中线等于斜边的一半．
四．矩形的判定与性质
（1）关于矩形，应从平行四边形的内角的变化上认识其特殊性：一个内角是直角的平行四边形，进一步研究其特有的性质：是轴对称图形、内角都是直角、对角线相等．同时平行四边形的性质矩形也都具有．
在处理许多几何问题中，若能灵活运用矩形的这些性质，则可以简捷地解决与角、线段等有关的问题．
（2）下面的结论对于证题也是有用的：①△OAB、△OBC都是等腰三角形；②∠OAB＝∠OBA，∠OCB＝∠OBC；③点O到三个顶点的距离都相等．

【考点剖析】
一．矩形的判定（共4小题）
1．（2021秋•天府新区期末）已知：如图，在△ABC中，AB＝AC，AD是∠BAC的平分线，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E．
求证：四边形ADCE为矩形；

【分析】根据三个角是直角是四边形是矩形即可证明；
【解答】证明：∵AB＝AC，AD是∠BAC的平分线，
∴AD⊥BC，∠BAD＝∠CAD．
∴∠ADC＝90°，
∵AN为△ABC的外角∠CAM的平分线，
∴∠MAN＝∠CAN．
∴∠DAE＝90°，
∵CE⊥AN，
∴∠AEC＝90°．
∴四边形ADCE为矩形．
【点评】本题考查矩形的判定、等腰三角形的性质、角平分线的定义等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
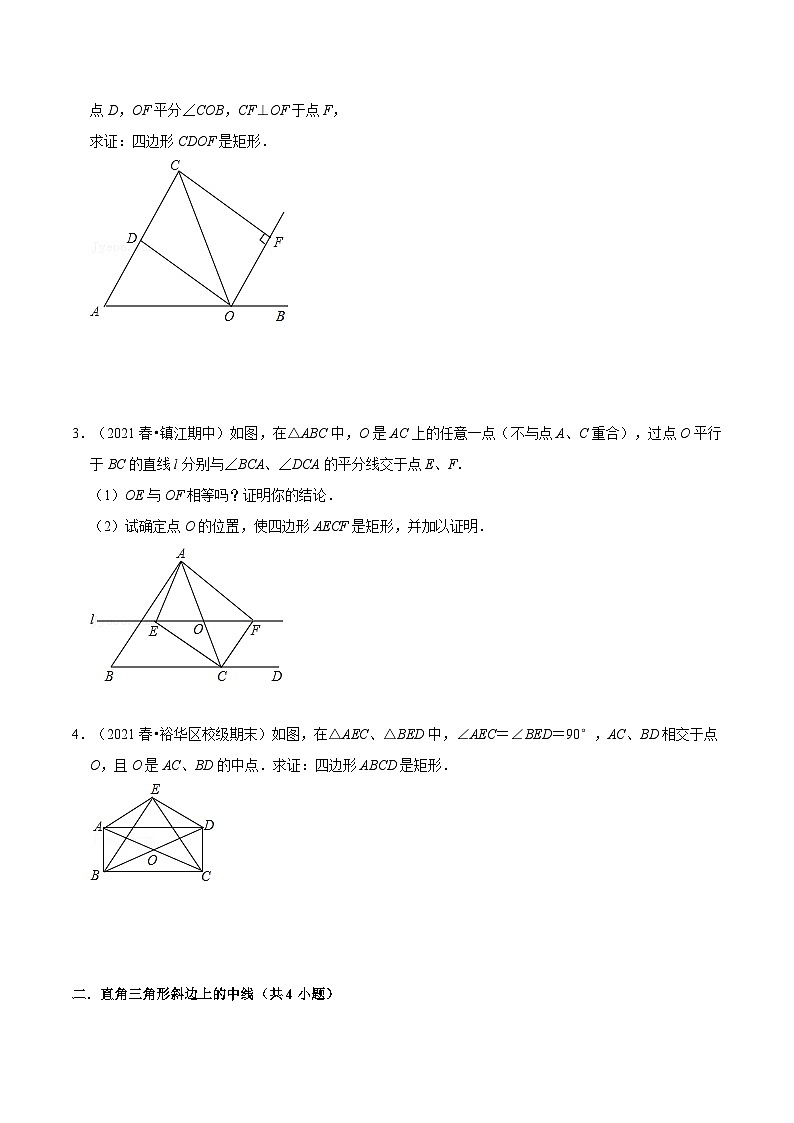
2．（2022春•思明区校级期中）如图所示，点O是线段AB上的一点，OA＝OC，OD平分∠AOC交AC于点D，OF平分∠COB，CF⊥OF于点F，
求证：四边形CDOF是矩形．

【分析】利用角平分线的性质、平角的定义可以求得∠DOF＝90°；由等腰三角形的“三合一”的性质可推知OD⊥AC，即∠CDO＝90°；根据已知条件“CF⊥OF”知∠CFO＝90°；则三个角都是直角的四边形是矩形；
【解答】证明：∵OD平分∠AOC，OF平分∠COB（已知），
∴∠AOC＝2∠COD，∠COB＝2∠COF，
∵∠AOC+∠BOC＝180°，
∴2∠COD+2∠COF＝180°，
∴∠COD+∠COF＝90°，
∴∠DOF＝90°；
∵OA＝OC，OD平分∠AOC（已知），
∴OD⊥AC，AD＝DC（等腰三角形的“三合一”的性质），
∴∠CDO＝90°，
∵CF⊥OF，
∴∠CFO＝90°
∴四边形CDOF是矩形；

【点评】本题考查了矩形的判定、角平分线的定义、等腰三角形的性质等知识，熟练掌握矩形的判定是解题的关键．
3．（2021春•镇江期中）如图，在△ABC中，O是AC上的任意一点（不与点A、C重合），过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F．
（1）OE与OF相等吗？证明你的结论．
（2）试确定点O的位置，使四边形AECF是矩形，并加以证明．

【分析】（1）根据平行线性质和角平分线定义推出∠OEC＝∠OCE，∠OFC＝∠OCF，根据等腰三角形的判定推出OE＝OC，OF＝OC即可；
（2）根据平行四边形的判定得出平行四边形AECF，根据对角线相等的平行四边形是矩形推出即可；
【解答】（1）解：相等；理由是：∵直线l∥BC，
∴∠OEC＝∠ECB，
∵CE平分∠ACB，
∴∠OCE＝∠BCE，
∴∠OEC＝∠OCE，
∴OE＝OC，
同理OF＝OC，
∴OE＝OF．

（2）解：O在AC的中点上时，四边形AECF是矩形，
理由是：∵OA＝OC，OE＝OF，
∴四边形AECF是平行四边形，
∵OE＝OF＝OC＝OA，
∴AC＝EF，
∴平行四边形AECF是矩形．
【点评】本题综合考查了平行四边形的性质和判定，矩形的判定，平行线的性质，角平分线定义等知识点的应用，题型较好，综合性比较强，难度也适中．
4．（2021春•裕华区校级期末）如图，在△AEC、△BED中，∠AEC＝∠BED＝90°，AC、BD相交于点O，且O是AC、BD的中点．求证：四边形ABCD是矩形．

【分析】连接EO，首先根据O为BD和AC的中点，在Rt△AEC中EO＝AC，在Rt△EBD中，EO＝BD，进而得到AC＝BD，再根据对角线相等的平行四边形是矩形可证出结论．
【解答】证明：连接EO，
∵O是AC、BD的中点，
∴AO＝CO，BO＝DO，
在Rt△EBD中，
∵O为BD中点，
∴EO＝BD，
在Rt△AEC中，∵O为AC中点，
∴EO＝AC，
∴AC＝BD，
又∵四边形ABCD是平行四边形，
∴平行四边形ABCD是矩形．

【点评】此题主要考查了矩形的判定，关键是掌握直角三角形斜边上的中线等于斜边的一半．
二．直角三角形斜边上的中线（共4小题）
5．（2022春•广丰区校级期中）如图，BD、CE是△ABC不同边上的高，点G、F分别是BC、DE的中点，试证明GF⊥DE．

【分析】连接EG、FG，根据直角三角形斜边上的中线等于斜边的一半可得DG＝EG＝BC，再根据等腰三角形三线合一的性质证明即可．
【解答】证明：如图，连接EG、DG，
∵BD、CE分别是△ABC的AC、AB边上的高，点G是BC的中点，
∴DG＝EG＝BC，
∵点F是DE的中点，
∴GF⊥DE．

【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形三线合一的性质，熟记性质并作出辅助线构造出等腰三角形是解题的关键．
6．（2022春•新邵县期中）如图，△ABC中，∠ACB＝90°，D是AB中点，过点B作直线CD的垂线，垂足为E．求证：∠EBC＝∠A．

【分析】根据直角三角形斜边上的中线等于斜边的一半得到CD＝BD，由等腰三角形的性质得到∠ABC＝∠ECB，根据余角的性质即可得到结论．
【解答】解：∵∠ACB＝90°，D是AB中点，
∴CD＝BD，
∴∠ABC＝∠ECB，
∵BE⊥CE，
∴∠E＝90°，
∴∠ECB+∠CBE＝∠ABC+∠A＝90°，
∴∠EBC＝∠A．
【点评】本题考查了直角三角形斜边上的中线等于斜边的一半，等腰三角形的性质，熟记直角三角形的性质是解题的关键．
7．（2021秋•镇海区校级期中）如图，在四边形ABCD中，∠BAD＝∠BCD＝90°，BC＝6，CD＝AC＝8，M、N分别是对角线BD、AC的中点，连结AM．
（1）求AM的长；
（2）求证：MN⊥AC；
（3）求MN的长．

【分析】（1）连接CM，根据勾股定理可得BD＝10，根据直角三角形斜边上的中线等于斜边的一半可得AM＝CM＝BM＝DM＝BD；
（2）根据等腰三角形三线合一的性质证明；
（3）利用勾股定理列式计算即可得解．
【解答】（1）解：如图，连接CM，

∵∠BAD＝∠BCD＝90°，M是BD的中点，
∴AM＝CM＝BM＝DM＝BD，
∵BC＝6，CD＝8，
∴BD＝＝10，
∴AM＝5；

（2）证明：∵∠BAD＝∠BCD＝90°，M是BD的中点，
∴AM＝CM＝BD，
∵N是AC的中点，
∴MN⊥AC；

（3）解：∵AC＝8，N是AC的中点，
∴AN＝×8＝4，
∴MN＝＝＝3．
【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形三线合一的性质，勾股定理，熟记性质与定理并作辅助线构造出等腰三角形是解题的关键．
8．（2021春•来宾月考）如图．△ABC中，∠C＝2∠B，D是BC上一点，且AD⊥AB，点E是BD的中点，连接AE．
（1）求证：BD＝2AC；
（2）若AE＝6.5，AD＝5，那么△ABE的周长是多少？

【分析】（1）根据直角三角形的性质得到EA＝BD＝EB，根据等腰三角形的性质和三角形的外角的性质证明；
（2）根据直角三角形的性质分别求出BC和BE，根据勾股定理求出AB，根据三角形的周长公式计算．
【解答】（1）证明：∵AD⊥AB，
∴∠BAD＝90°，又点E是BD的中点，
∴EA＝BD＝EB，
∴∠EAB＝∠EBA，
∴∠AEC＝2∠B，又∠C＝2∠B，
∴∠AEC＝∠C，
∴AE＝AC，
∴BD＝2AC；
（2）解：∵∠BAD＝90°，点E是BD的中点，
∴BD＝2AE＝13，EA＝EB＝6.5，
由勾股定理得，AB＝＝＝12，
∴△ABE的周长＝AB+AE+BE＝12+6.5+6.5＝25．
【点评】本题考查的是直角三角形的性质，勾股定理的应用，在直角三角形中，斜边上的中线等于斜边的一半．
三．矩形的性质（共4小题）
9．（2022•长清区二模）已知：如图，在矩形ABCD中，点M、N在边AD上，且AM＝DN，求证：BN＝CM．

【分析】由矩形的性质可得出BA＝CD、∠A＝∠D，由AM＝DN可得出AN＝DM，进而即可证出△ABN≌△DCM（SAS），根据全等三角形的性质可证出BN＝CM．
【解答】证明：∵四边形ABCD为矩形，
∴BA＝CD，∠A＝∠D．
∵AM＝DN，
∴AN＝DM．
在△ABN和△DCM中，，
∴△ABN≌△DCM（SAS），
∴BN＝CM．
【点评】本题考查了矩形的性质以及全等三角形的判定与性质，利用全等三角形的判定定理SAS证出△ABN≌△DCM是解题的关键．
10．（2021春•邳州市期中）已知：如图，矩形ABCD的对角线AC、BD相交于点O，且AC＝2AB．求证：△AOB是等边三角形．

【分析】根据矩形的性质可知AO＝BO＝CO＝DO，进而可得AB＝AO+BO，即可证明其为等边三角形；或者利用2AB＝AC，得∠ACB＝30°，∠BAC＝60°，结合AB＝AO证明其为等边三角形．
【解答】解：∵∠ABC＝90°，AC＝2AB，
∴∠ACB＝30°，∠BAC＝60°，
∵四边形ABCD为矩形，
∴AO＝CO，
∴AB＝AO＝CO，
∴△AOB是等边三角形．
【点评】本题考查矩形的性质，熟练掌握矩形对角线互相平分且相等的性质是解题关键．
11．（2021春•建平县期末）把一张长方形（对边平行）纸条按如图所示折叠．判断∠1与∠2相等吗？说明理由．

【分析】由平行线的性质可得∠1＝∠CBA'，由折叠的性质可得∠CBA'＝∠2，即可求解．
【解答】解：∠1＝∠2，理由如下：
∵四边形ABCD是矩形，
∴CF∥BD，
∴∠1＝∠CBA'，
∵将长方形折叠，
∴∠CBA'＝∠2，
∴∠1＝∠2．
【点评】本题考查了矩形的性质，折叠的性质，平行线的性质，灵活运用这些性质解决问题是解题的关键．
12．（2021春•柳南区校级期末）如图，矩形ABCD的对角线AC、BD相交于点O，点E、F在AC上，AE＝CF．
（1）求证：四边形BEDF是平行四边形；
（2）若AD＝2，∠AOB＝120°，求AB的长．

【分析】（1）根据平行四边形的判定即可求出答案．
（2）根据矩形的性质以及含30度角的直角三角形的性质即可求出答案．
【解答】解：（1）在矩形ABCD中，
∴OA＝OB＝OC＝OD，
∵AE＝CF，
∴OE＝OF，
∴四边形BEDF是平行四边形．
（2）由（1）可知：OA＝OB，
∵∠AOB＝120°，
∴∠DBA＝30°，
∵AD＝2，
∴AB＝AD＝6．
【点评】本题考查矩形，解题的关键是熟练运用矩形的性质以及平行四边形的判定，本题属于基础题型．
四．矩形的判定与性质（共4小题）
13．（2022•盐池县二模）如图所示，点O是菱形ABCD对角线的交点，CE∥BD，EB∥AC，连接OE，交BC于F
（1）求证：OE＝CB；
（2）如果OC：OB＝1：2，OE＝2，求菱形ABCD的面积．

【分析】（1）由CE∥BD、EB∥AC可得出四边形OBEC为平行四边形，由菱形的性质可得出∠BOC＝90°，进而可得出四边形OBEC为矩形，根据矩形的性质即可证出OE＝CB；
（2）设OC＝x，则OB＝2x，利用勾股定理可得出BC＝x，结合BC＝OE＝2，可求出x的值，进而可得出OC、OB的值，再利用菱形的面积公式即可求出结论．
【解答】（1）证明：∵CE∥BD，EB∥AC，
∴四边形OBEC为平行四边形．
∵四边形ABCD为菱形，
∴AC⊥BD，
∴∠BOC＝90°，
∴四边形OBEC为矩形，
∴OE＝CB．
（2）解：设OC＝x，则OB＝2x，
∴BC＝＝x．
∵BC＝OE＝2，
∴x＝2，
∴OC＝2，OB＝4，
∴S菱形ABCD＝AC•BD＝2OC•OB＝16．

【点评】本题考查了矩形的判定与性质、勾股定理以及菱形的性质，解题的关键是：（1）证出四边形OBEC为矩形；（2）利用勾股定理结合OE的长度，求出OB、OC的值．
14．（2021春•黄山期末）如图，在平行四边形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使CF＝BE，连接DF．
（1）求证：四边形ADFE是矩形；
（2）连接OF，若AD＝6，EC＝4，∠ABF＝60°，求OF的长度．

【分析】（1）由在平行四边形性质得到AB∥DC且AB＝DC，由平行线的性质得到∠ABE＝∠DCF，根据三角形的判定可证得△ABE≌△DCF，由全等三角形的性质得到AE＝DF，∠AEB＝∠DFC＝90°，可得AE∥DF，根据矩形的判定即可得到结论；
（2）由矩形的性质得到EF＝AD＝6，进而求得BE＝CF＝2，BF＝8，由∠ABE＝60°可求得AB＝2BE＝4，由勾股定理可求得DF＝AE＝2，BD＝2，由平行四边形性质得OB＝OD，由直角三角形斜边的中线等于斜边的一半即可得到结论．
【解答】（1）证明：∵在平行四边形ABCD中，
∴AB∥DC且AB＝DC，
∴∠ABE＝∠DCF，
在△ABE和△DCF中，，
∴△ABE≌△DCF（SAS），
∴AE＝DF，∠AEB＝∠DFC＝90°，
∴AE∥DF，
∴四边形ADFE是矩形；

（2）解：由（1）知：四边形ADFE是矩形，
∴EF＝AD＝6，
∵EC＝4，
∴BE＝CF＝2，
∴BF＝8，
Rt△ABE中，∠ABE＝60°，
∴AB＝2BE＝4，
∴DF＝AE＝，
∴BD＝＝2，
∵四边形ABCD是平行四边形，
∴OB＝OD，
∴OF＝BD＝．
【点评】本题考查了平行四边形的性质，矩形的判定和性质，勾股定理，直角三角形斜边上的中线性质等知识；正确的识别图形是解题的关键．
15．（2021春•无为市期末）如图，▱ABCD的对角线AC，BD相交于点O，△OAB是等边三角形．
（1）求证：▱ABCD为矩形；
（2）若AB＝4，求▱ABCD的面积．

【分析】（1）根据题意可求OA＝OB＝DO，∠AOB＝60°，可得∠BAD＝90°，即结论可得
（2）根据勾股定理可求AD的长，即可求▱ABCD的面积．
【解答】解（1）∵△AOB为等边三角形∴∠BAO＝60°＝∠AOB，OA＝OB
∵四边形ABCD是平行四边形
∴OB＝OD，
∴OA＝OD
∴∠OAD＝30°，
∴∠BAD＝30°+60°＝90°
∴平行四边形ABCD为矩形；
（2）在Rt△ABC中，∠ACB＝30°，
∴AB＝4，BC＝AB＝4
∴▱ABCD的面积＝4×4＝16
【点评】本题考查了矩形的性质和判定，等边三角形的性质，灵活运用这些性质解决问题是本题的关键．
16．（2021•八步区模拟）如图，在▱ABCD中，过点D作DE⊥AB于点E，点F在边CD上，CF＝AE，连接AF，BF．
（1）求证：四边形BFDE是矩形；
（2）已知∠DAB＝60°，AF是∠DAB的平分线，若AD＝3，求DC的长度．

【分析】（1）由题意可证四边形DFBE是平行四边形，且DE⊥AB，可得结论
（2）根据直角三角形的边角关系可求DE的长度，则可得BF的长度，即可求CD的长度．
【解答】证明（1）∵四边形ABCD是平行四边形
∴DC∥AB，DC＝AB
∵CF＝AE
∴DF＝BE且DC∥AB
∴四边形DFBE是平行四边形
又∵DE⊥AB
∴四边形DFBE是矩形；
（2）∵∠DAB＝60°，AD＝3，DE⊥AB
∴AE＝，DE＝AE＝
∵四边形DFBE是矩形
∴BF＝DE＝
∵AF平分∠DAB
∴∠FAB＝∠DAB＝30°，且BF⊥AB
∴AB＝BF＝
∴CD＝
【点评】本题考查了矩形的判定和性质，平行四边形的性质，熟练运用这些性质解决问题是本题的关键．
【过关检测】
一．选择题（共3小题）
1．（2022春•綦江区期中）矩形具有而菱形不具有的性质是（　　）
A．两组对边分别相等 B．对角线互相平分
C．对角线相等 D．对角线互相垂直
【分析】根据矩形的性质和菱形的性质即可解决问题．
【解答】解：矩形的性质是：①矩形的四个角都是直角，②矩形的对边相等且互相平行，③矩形对角线相等且互相平分；
菱形的性质是：①菱形的四条边都相等，菱形的对边互相平行；②菱形的对角相等，③菱形的对角线互相平分且垂直，并且每条对角线平分一组对角，
所以矩形具有而菱形不具有的性质是对角线相等，
故选：C．
【点评】本题考查了矩形的性质和菱形的性质，能熟记知识点是解此题的关键．
2．（2022春•溆浦县期中）已知矩形ABCD的周长为16，AB＝5，则BC等于（　　）
A．3 B．5 C．6 D．11
【分析】根据矩形的周长公式即可得到结论．
【解答】解：∵矩形ABCD的周长为16，
∴BC＝×（16﹣2×5）＝3，
故选A．
【点评】本题考查了矩形的性质，熟练掌握矩形的周长公式是解题的关键．
3．（2022春•东城区期中）如图，矩形OABC的顶点B的坐标为（2，3），则AC长为（　　）

A． B． C．5 D．4
【分析】由两点距离公式可求OB的长，由矩形的性质可得AC＝OB，即可求即解．
【解答】解：如图，连接OB，

∵点B的坐标为（2，3），
∴OB＝＝，
∵∵四边形ABCO是矩形，
∴AC＝OB＝，
故选：A．
【点评】本题考查了矩形的性质，两点距离公式，掌握矩形的性质是解题的关键．
二．填空题（共7小题）
4．（2022春•大丰区期中）已知矩形ABCD中，若AC＝8，则BD＝　8　．
【分析】根据矩形的对角线相等即可解决问题．
【解答】解：∵四边形ABCD是矩形，
∴BD＝AC＝8．
故答案为：8．
【点评】本题考查了矩形的对角线相等的性质，比较简单，熟记性质是解题的关键．
5．（2022•前进区一模）如图，已知四边形ABCD为平行四边形，对角线AC与BD交于点O，试添加一个条件 　AC＝BD　，使▱ABCD为矩形．

【分析】根据对角线相等的平行四边形是矩形可添加的条件是AC＝BD．
【解答】解：∵AC＝BD，四边形ABCD为平行四边形，
∴四边形ABCD为矩形．
故答案为：AC＝BD．
【点评】本题考查矩形的判定，熟练掌握矩形的判定方法是解决本题的关键．
6．（2022春•蓝山县期中）直角三角形斜边上的中线与高的长分别是6cm、5cm，则它的面积是　30　 cm2．
【分析】根据直角三角形斜边上的中线等于斜边的一半求出斜边，再利用三角形的面积公式列式计算即可得解．
【解答】解：∵直角三角形斜边上的中线长是6cm，
∴斜边长＝2×6＝12cm，
∵直角三角形斜边上的高的长是5cm，
∴直角三角形的面积＝×12×5＝30（cm2）．
故答案为：30．
【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，三角形的面积，熟记性质并求出斜边的长是解题的关键．
7．（2022春•盐都区期中）如图，在矩形ABCD中，AB＝3，对角线AC的长为5，作AC的垂直平分线交BC于点M，连接AM，则△ABM的周长为 　7　．

【分析】由勾股定理可求BC的长，由线段垂直平分线的性质可得AM＝CM，可求解．
【解答】解：∵四边形ABCD是矩形，
∴∠B＝90°，
∴BC＝＝＝4，
∵AC的垂直平分线交BC于点M，
∴AM＝CM，
∴△ABM的周长＝AB+BM+AM＝AB+BC＝7，
故答案为：7．
【点评】本题考查了矩形的性质，线段垂直平分线的性质；熟练掌握矩形的性质是解决问题的关键．
8．（2022春•西城区校级期中）小明在探究“四边形的不稳定性”活动中，将四根木条用钉子钉成一个矩形框架ABCD，如图所示．扭动矩形框架，观察矩形ABCD的变化，下列判断：
①四边形ABCD由矩形变为平行四边形
②A、C两点之间的距离不变；
③四边形ABCD的面积不变；
④四边形ABCD的周长不变
正确的是　①④　（填序号）

【分析】根据四边形的不稳定性和矩形的性质以及矩形和平行四边形之间的关系进行判断即可确定正确的答案．
【解答】解：①四边形ABCD由矩形变为平行四边形，正确；
②A、C两点之间的距离会发生变化，故原命题错误；
③四边形ABCD由矩形变为平行四边形后底边不变，高逐渐的减小，故原命题错误；
④四边形ABCD的周长不变，正确，
正确的有①④，
故答案为：①④．
【点评】考查了矩形的性质以及矩形的判定的知识，解题的关键是了解矩形与平行四边形之间的关系，难度不大．
9．（2022•长春模拟）如图所示，四边形ABCD为矩形，AE⊥EG，已知∠1＝25°，则∠2＝　115°　

【分析】由矩形的性质可得AD∥BC，可得∠DFE＝∠2，由三角形的外角性质可求∠2的度数．
【解答】解：∵四边形ABCD是矩形
∴AD∥BC
∴∠DFE＝∠2
∵∠DFE＝∠1+∠E＝115°
∴∠2＝115°
故答案为：115°
【点评】本题考查了矩形的性质，三角形外角性质，熟练运用矩形的性质是本题的关键．
10．（2022春•宁津县期中）工人师傅常常通过测量平行四边形零件的对角线是否相等来检验零件是否为矩形，请问工人师傅此种检验方法依据的道理是　对角线相等的平行四边形是矩形　．
【分析】根据矩形的判定定理（对角线相等的平行四边形是矩形）得到矩形ABCD可得到答案．
【解答】解：∵四边形ABCD是平行四边形，AC＝BD，
∴平行四边形ABCD是矩形，
故答案为：对角线相等的平行四边形是矩形．

【点评】本题主要考查对矩形的性质和判定的理解和掌握，能熟练地运用矩形的性质解决实际问题是解此题的关键．
三．解答题（共6小题）
11．（2021•历城区二模）如图，矩形ABCD中，E、F分别为边AD和BC上的点，BE＝DF，求证：DE＝BF．

【分析】先利用四边形ABCD是矩形，得出AB＝CD，AD＝BC，∠A＝∠D＝90°，然后证明△ABE≌△CDF即可．
【解答】证明：∵四边形ABCD是矩形，
∴AB＝CD，AD＝BC，∠A＝∠C＝90°，
在Rt△ABE和Rt△CDF中，
，
∴Rt△ABE≌Rt△CDF（HL），
∴AE＝CF，
∴DE＝BF．
【点评】本题考查矩形的性质以及直角三角形全等的判定，关键是对知识的综合运用．
12．（2021•福建模拟）如图，在矩形ABCD中，BF＝CE，求证：AE＝DF．

【分析】欲证明AE＝DF，只要证明△ABE≌△DCF即可．
【解答】证明：∵四边形ABCD是矩形，
∴AB＝DC，
∠B＝∠C＝90°，
∵BF＝CE，
∴BE＝CF，
在△ABE和△DCF中，
，
∴△ABE≌△DCF，
∴AE＝DF．
【点评】本题考查矩形的性质，全等三角形的判定和性质等知识，解题的关键是熟练掌握矩形的性质，正确寻找全等三角形解决问题，属于中考常考题型．
13．（2021秋•金安区校级月考）已知：如图，在矩形ABCD中，AC，BD交于点E．
（1）作EF垂直BC于点F，求证：点F是线段BC的2等分点；
（2）连接DF交AC于点G，作CH垂直BC于点H，求证：点H是线段BC的3等分点；
（3）你能在图中作出线段BC的一个4等分点吗？

【分析】（1）由矩形的性质可知AE＝EC，由平行线分线段成比例定理可知BF＝FC；
（2）先证明△EFG∽△CDG，从而可得到EG：GC＝1：2，故此CG：AC＝1：3，然后由平行线分线段成比例定理可求得CH：CB＝1：3；
（3）过点E作EP⊥DC，连接FP交AC于点Q，过点Q作QM⊥BC，垂足为M则点M为BC的一个四等分点．
【解答】解：（1）∵四边形ABCD是矩形，
∴点E为AC的中点．
∴AE＝EC．
∵EF⊥BC，AB⊥BC，
∴EF∥AB．
∴CF：FB＝CE：EA＝1．
∴CF＝FB．
∴点F是BC的中点．
（2）∵AE＝EC，BF＝FC，
∴EF是△BCD的中位线．
∴EF＝．
∵EF⊥BC，DC⊥BC，
∴△EFG∽△CDG．
∴．
∴．
∵GH∥AB，
∴．
∴点H是BC的三等分点．
（3）如图所示：过点E作EP⊥DC于P，连接FP交CE于Q，过Q做QM⊥BC，M为BC的四等分点．

【点评】本题主要考查的是矩形的性质、平行线分线段成比例定理、相似三角形的性质可判定，由△EFG∽△CDG求得QC＝2EG，从而得到AC＝3CG是解题的关键．
14．（2021春•中山区期末）在△ABC中，∠ACB＝90°，CD⊥AB于点D，∠ACD＝3∠BCD，E是AB的中点，求∠ECD的度数．

【分析】先求出∠BCD和∠ACD，再根据直角三角形两锐角互余求出∠B，根据直角三角形斜边上的中线等于斜边的一半可得CE＝BE，根据等边对等角可得∠BCE＝∠B，再求出∠ECD＝45°．
【解答】解：∵∠ACB＝90°，∠ACD＝3∠BCD，
∴∠BCD＝90°×＝22.5°，
∠ACD＝90°×＝67.5°，
∵CD⊥AB，
∴∠B＝90°﹣22.5°＝67.5°，
∵E是AB的中点，∠ACB＝90°，
∴CE＝BE，
∴∠BCE＝∠B＝67.5°，
∴∠ECD＝∠BCE﹣∠BCD＝67.5°﹣22.5°＝45°．
【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形的性质，熟记性质并准确识图，理清图中各角度之间的关系是解题的关键．
15．（2021秋•榆阳区校级月考）长方形ABCD的长与宽分别是6和3，直接写出下列各图中A，B，C，D各个顶点的坐标．

【分析】由矩形的性质可得AB＝CD＝6，BC＝AD＝3，AB∥CD，AD∥BC，即可求解．
【解答】解：∵四边形ABCD是矩形，
∴AB＝CD＝6，BC＝AD＝3，AB∥CD，AD∥BC，
∴点C（﹣2，0），点D（4，0），点A（4，3），点B（﹣2，3）．
【点评】本题考查了矩形的性质，坐标与图形性质，掌握矩形的性质是解题的关键．
16．（2020秋•柳南区校级期末）如图，矩形ABCD，AB＝6，BC＝4，过对角线BD中点O的直线分别交AB、CD边于点E，F．
（1）求证：四边形DEBF是平行四边形；
（2）当四边形DEBF是菱形时，求菱形的边长．

【分析】（1）根据平行四边形ABCD的性质，判定△BOE≌△DOF（ASA），得出四边形BEDF的对角线互相平分，进而得出结论；
（2）在Rt△ADE中，由勾股定理得出方程，解方程求出DF的长即可求得菱形的边长．
【解答】（1）证明：∵四边形ABCD是矩形，O是BD的中点，
∴∠A＝90°，AD＝BC＝4，AB∥DC，OB＝OD，
∴∠OBE＝∠ODF，
∴△BOE≌△DOF（ASA），
∴EO＝FO，
∴四边形BEDF是平行四边形；
（2）解：当四边形BEDF是菱形时，BD⊥EF，
设BE＝x，则 DE＝x，AE＝6﹣x，
在Rt△ADE中，DE2＝AD2+AE2，
∴x2＝42+（6﹣x）2，
解得：x＝，
∴菱形的边长为．
【点评】本题主要考查了矩形的性质，菱形的性质、勾股定理、全等三角形的判定与性质，熟练掌握矩形的性质和勾股定理，证明三角形全等是解决问的关键．