9初中数学.全等与几何变换.第09讲

这是一份9初中数学.全等与几何变换.第09讲，文件包含初中数学全等与几何变换第09讲教师版doc、初中数学全等与几何变换第09讲学生版doc等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。
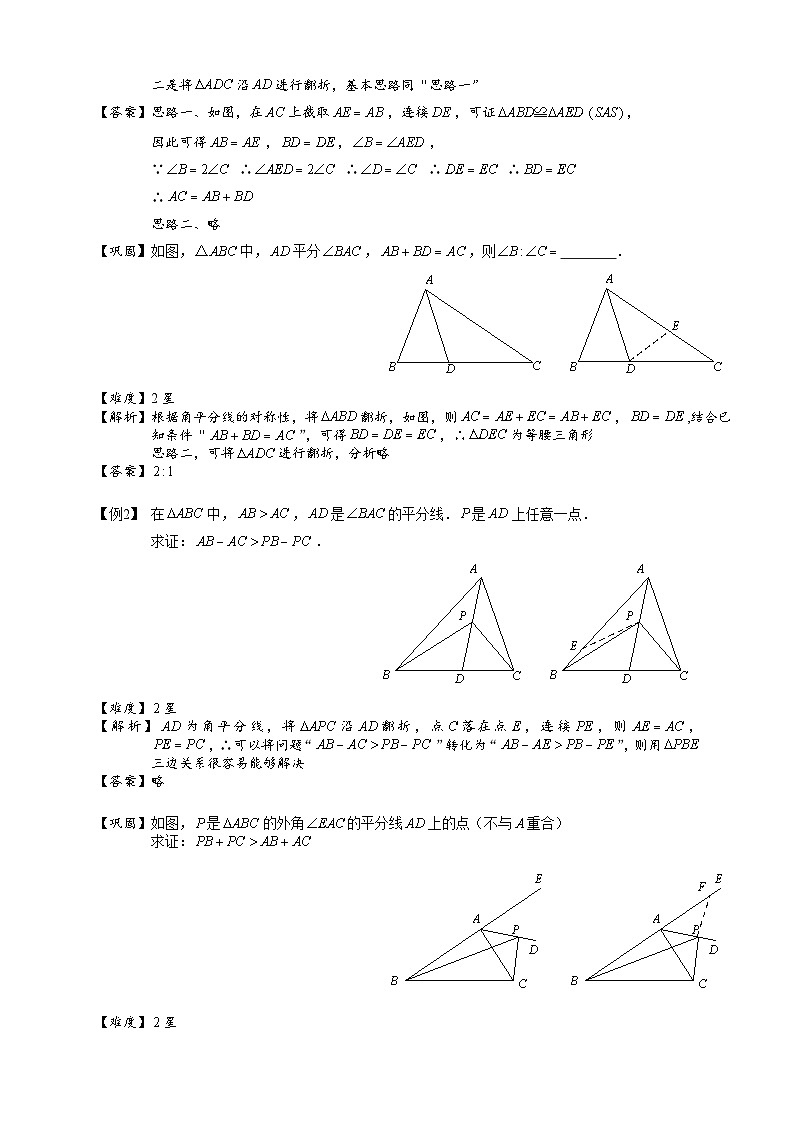
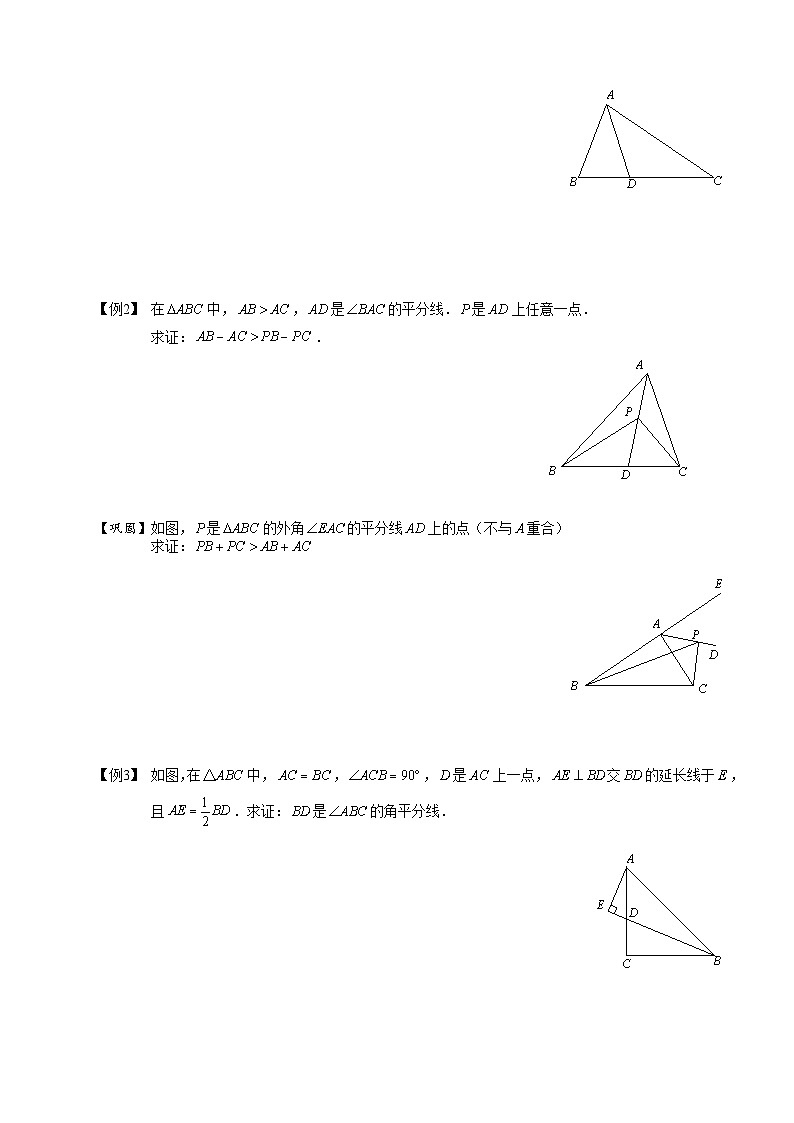
       内容基本要求略高要求较高要求轴对称了解图形的轴对称，理解对应点所连的线段被对称轴垂直平分性质；了解物体的镜面对称能按要求作出简单平面图形经过一次或两次轴对称后的图形；掌握简单图形之间的轴对称关系，并能指出对称轴；掌握基本图形（等腰三角形、矩形、菱形、等腰梯形、正多边形、圆）的轴对称性及相关性质。能运用轴对称进行图案设计旋转了解图形的旋转，理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质；会识别中心对称图形能按要求作出简单平面图形旋转后的图形，能依据旋转前、后的图形，指出旋转中心和旋转角能运用旋转的知识解决简单问题；平移了解图形平移，理解平移中对应点连线平行（或在同一条直线上）且相等的性质能按要求作出简单平面图形平移后的图形；能依据平移前后的图形，指出平移的方向和距离能运用平移的知识解决简单的计算问题； 模块一  全等三角形与轴对称 ☞角平分线类 “角”是轴对称图形，对称轴为角平分线所在的直线。因此在遇见与角平分线有关问题的时候，可以有下面几个基本解题思路：①平分角；②角平分线上点到角两边的距离相等；③沿角平分线进行翻折。 【例1】         如图，在中，，为的平分线．求证：．    【巩固】如图，中，平分，，则        ．    【例2】         在中，，是的平分线．是上任意一点．求证：． 【巩固】如图，是的外角的平分线上的点（不与重合）求证：  【例3】         如图，在中，，，是上一点，交的延长线于，且．求证：是的角平分线．   ☞垂直平分线类垂直平分线：“垂直平分线上点到线段两个端点的距离相等”，主要是转化线段之间的关系，尤其是在轴对称有关作图中，应用更为广泛 【例4】         如图，的两边、的垂直平分线分别交于、，若,则的度数是         【巩固】如图中，平分，且平分，于，于. ⑴说明的理由；⑵如果，，求，的长.    ☞构造等腰三角形类构造等腰三角形类的主要方法有两种：①是将直角三角形沿着某一直角边翻折；②是截取等长线段 【例5】         如图，在中，，于，且，那么的度数是_______  【巩固】如图，在中，于，．求证：．    ☞构造等边三角形类构造等边三角形类的方式主要有两种：①直接以某一线段长为边，直接构造等边三角形；②作等腰三角形，然后利用题目给出的特殊角，如，证明此等腰三角形为等边三角形 【例6】         如图，在中，，是外的一点，且，．求证：．    【巩固】如图，已知，且．求证：是等腰三角形．       模块二  全等三角形与旋转 ☞全等三角形与旋转的性质一般涉及到旋转有关问题时，都会用到:旋转前后，图形对应全等，由此转化线段与角的对应关系 【例7】         如图，将绕点按逆时针方向旋转至，使点恰好落在边上，已知， ，则的长是________【巩固】如图，将绕着点按顺时针方向旋转，点落在点位置，点落在点位置，若，则 【例8】         如图，在上，在上，且，，则的长等于（   ）A.              B.            C.            D. ☞倍长中线类倍长中线是我们耳熟能详的一种辅助线的作法，其实此作法最主要是通过旋转的方式，构造出一对“8”字型全等三角形，从而转化线段与角的数量关系 【例9】         如图，已知为边的中点，，则（    ）A．大于B．小于C．等于D．与的大小关系无法确定  【巩固】在后面的学习中，我们会学习到与直角三角形斜边上有关的性质：“直角三角形斜边上的中线等于斜边的一半”，用数学语言改编如下：已知：在中，，为斜边的中点，证明:    【例10】     在《四边形》这一章中，我们会学习到中位线的概念以及性质中位线的概念：三角形两边中点的连线，我们称之为三角形的中位线中位线的性质：三角形的中位线平行于第三边，且等于第三边的一半用数学语言改编如下：如图，在中，为的中点，为的中点证明：，【巩固】两个全等的含、角的三角板和三角板，如图所示放置，、、三点在一条直线上，连结，取的中点，连结、，试判断的形状，并说明理由．   ☞一般等腰三角形旋转 一般等腰三角形旋转的问题主要有：①通过对等腰三角形旋转，构造全等三角形；②通过对一般三角形旋转构造等腰三角形 【例11】     如图，中，，,将绕点逆时针旋转到如图所示位置求证：，   【巩固】如图，是边长为1的正三角形，是顶角为的等腰三角形，以为顶点作一个的，点分别在上，则的周长是      ．     ☞等腰直角三角形旋转 等腰直角三角形旋转有关问题要充分考虑到：“边相等”“角相等”，还有斜边上的中线，这条特殊的线段，尤其是涉及到斜边中点的时候，基本上都会连接这条中线 【例12】     已知：三角形中，，，为的中点．（1）如图，分别是上的点，且，求证：为等腰直角三角形．（2）若分别为延长线上的点，仍有，其他条件不变，那么，是否仍为等腰直角三角形？证明你的结论．         【巩固】如图，在中，＝，＝，为上任意一点，且⊥于，⊥于，为的中点，试判断是什么形状的三角形，并证明你的结论．     ☞等边三角形旋转 【例13】     复习“全等三角形”的知识时，老师布置了一道作业题：“如图①，已知中，，是内任意一点，将绕点顺时针旋转至，使，连接、，则。”小亮是个爱动脑筋的同学，他通过对图①的分析，证明了，从而得，之后，他将点移到等腰三角形之外，原题中其他条件不变，发现“”仍然成立，请你就图②给出证明。    【巩固】如图，已知四边形中，，，证明：． ☞三垂直全等及三垂直的变形【例14】     在中，，，直线经过点，且于，于．⑴当直线绕点旋转到图①的位置时，求证：；    ⑵当直线绕点旋转到图②的位置时，求证：；      ⑶当直线绕点旋转到图③的位置时，试问：、、有怎样的等量关系？请写出这个等量关系，并加以证明．        【巩固】如图，在等腰中，，为上一点，，，那么等于（    ）A．     B．     C．      D．【巩固】如图，是经过顶点的一条直线，，、分别是直线上两点，且．（1）若直线经过的内部，且、在直线上，请解决下面两个问题：①如图①，若，，则        ；        （填“”、“”、“”）；②如图②，若，请添加一个关于与关系的条件        ，使①中的两个结论仍然成立，并证明这两个结论． （2）如图③，若直线经过的外部，，请提出、、三条线段数量关系的合理猜想（不要求证明）．      模块三  全等三角形与平移平移的基本思路是通过平移，将有关系但又不在一起的量集中起来，且对应边平行且相等 【例15】     如图所示，两条长度为的线段和相交于点，且，求证：．   【巩固】如图所示，在的边上取两点、，且．求证：．                         点是四边形的边的中点，，证明：                          如图，在中，，是外的一点，且，．求证：．    1．通过本堂课你学会了                                                   ．2．掌握的不太好的部分                                                   ．3．老师点评：①                                                         ．     ②                                                         ．             ③                                                         ．1．   如图，是的角平分线， ， ,判断的度数并说明理由。答：=              证明：