高中数学人教A版（2019）必修第二册《第九章 统计》单元测试 （含解析）

这是一份高中数学人教A版（2019）必修第二册《第九章 统计》单元测试 （含解析），共17页。
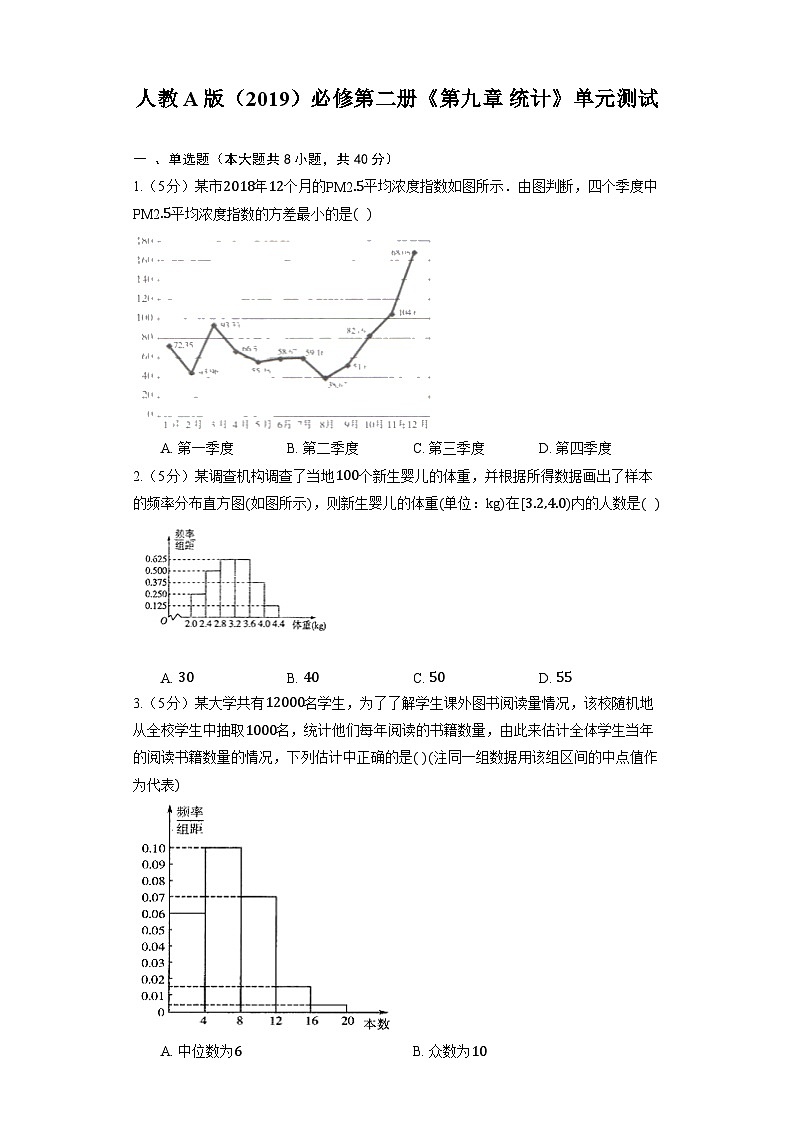
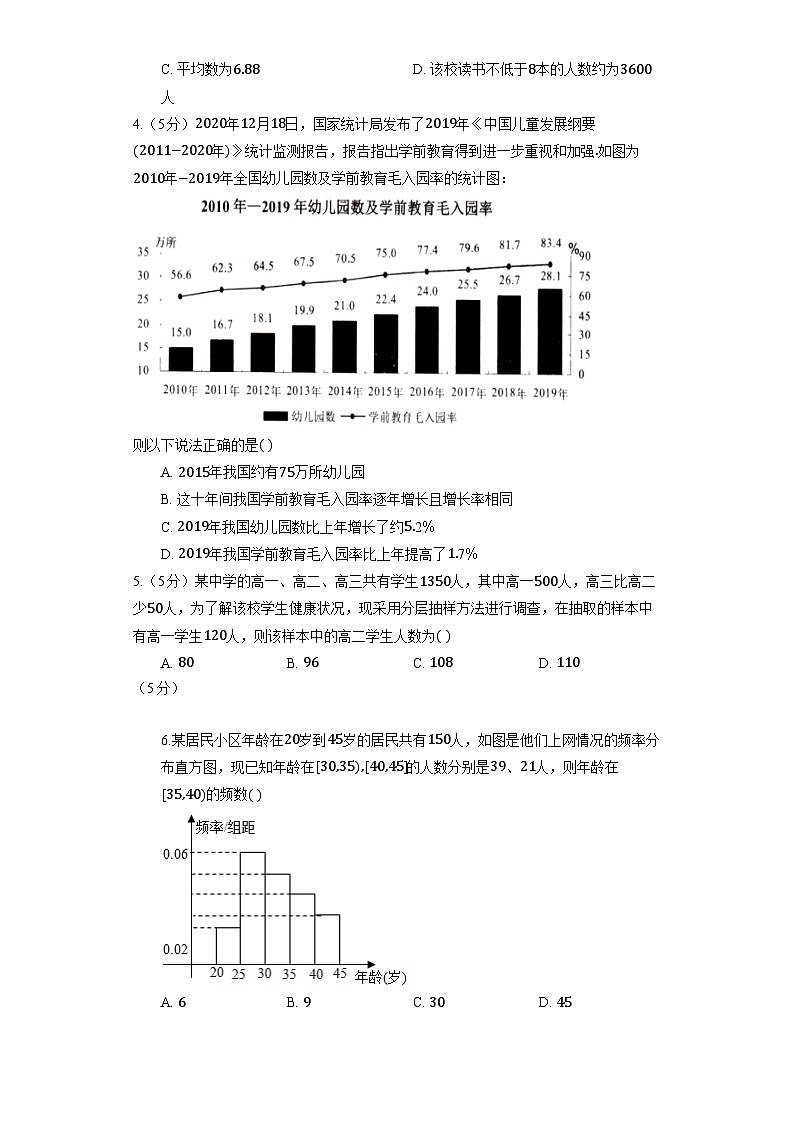
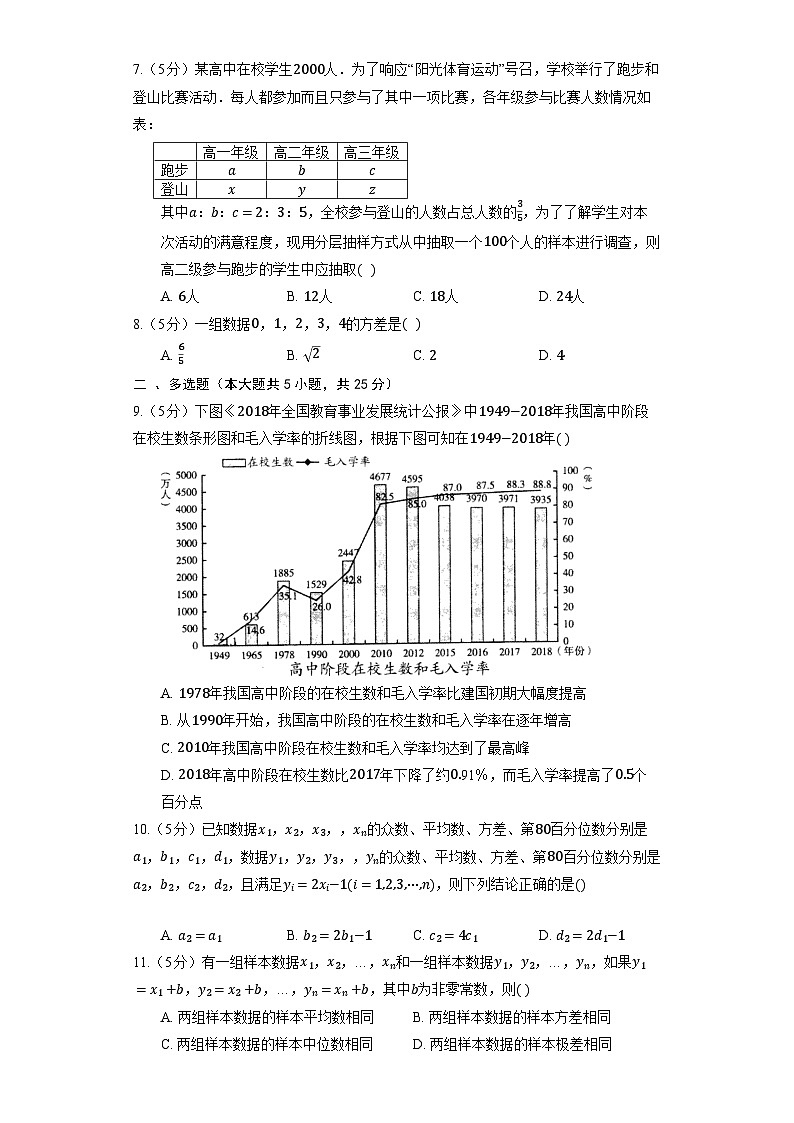
 人教A版（2019）必修第二册《第九章 统计》单元测试  一 、单选题（本大题共8小题，共40分）1.（5分）某市年个月的平均浓度指数如图所示．由图判断，四个季度中平均浓度指数的方差最小的是A. 第一季度 B. 第二季度 C. 第三季度 D. 第四季度2.（5分）某调查机构调查了当地个新生婴儿的体重，并根据所得数据画出了样本的频率分布直方图如图所示，则新生婴儿的体重单位：在内的人数是    A.  B.  C.  D. 3.（5分）某大学共有名学生，为了了解学生课外图书阅读量情况，该校随机地从全校学生中抽取名，统计他们每年阅读的书籍数量，由此来估计全体学生当年的阅读书籍数量的情况，下列估计中正确的是注同一组数据用该组区间的中点值作为代表A. 中位数为 B. 众数为C. 平均数为 D. 该校读书不低于本的人数约为人4.（5分）年月日，国家统计局发布了年《中国儿童发展纲要年》统计监测报告，报告指出学前教育得到进一步重视和加强如图为年年全国幼儿园数及学前教育毛入园率的统计图：  则以下说法正确的是A. 年我国约有万所幼儿园B. 这十年间我国学前教育毛入园率逐年增长且增长率相同C. 年我国幼儿园数比上年增长了约D. 年我国学前教育毛入园率比上年提高了5.（5分）某中学的高一、高二、高三共有学生人，其中高一人，高三比高二少人，为了解该校学生健康状况，现采用分层抽样方法进行调查，在抽取的样本中有高一学生人，则该样本中的高二学生人数为A.  B.  C.  D. （5分）  6.某居民小区年龄在岁到岁的居民共有人，如图是他们上网情况的频率分布直方图，现已知年龄在的人数分别是、人，则年龄在的频数A.  B.  C.  D. 7.（5分）某高中在校学生人．为了响应“阳光体育运动”号召，学校举行了跑步和登山比赛活动．每人都参加而且只参与了其中一项比赛，各年级参与比赛人数情况如表： 高一年级高二年级高三年级跑步登山其中：：：：，全校参与登山的人数占总人数的，为了了解学生对本次活动的满意程度，现用分层抽样方式从中抽取一个个人的样本进行调查，则高二级参与跑步的学生中应抽取A. 人 B. 人 C. 人 D. 人8.（5分）一组数据，，，，的方差是A.  B.  C.  D. 二 、多选题（本大题共5小题，共25分）9.（5分）下图《年全国教育事业发展统计公报》中年我国高中阶段在校生数条形图和毛入学率的折线图，根据下图可知在年A. 年我国高中阶段的在校生数和毛入学率比建国初期大幅度提高B. 从年开始，我国高中阶段的在校生数和毛入学率在逐年增高C. 年我国高中阶段在校生数和毛入学率均达到了最高峰D. 年高中阶段在校生数比年下降了约，而毛入学率提高了个百分点10.（5分）已知数据，，，，的众数、平均数、方差、第百分位数分别是，，，，数据，，，，的众数、平均数、方差、第百分位数分别是，，，，且满足，则下列结论正确的是  A.  B.  C.  D. 11.（5分）有一组样本数据，，…，和一组样本数据，，…，，如果，，…，，其中为非零常数，则A. 两组样本数据的样本平均数相同 B. 两组样本数据的样本方差相同C. 两组样本数据的样本中位数相同 D. 两组样本数据的样本极差相同12.（5分）如图，海水养殖厂进行某水产品的新旧网箱养殖方法产量对比，收获时各随机抽取了个网箱，测量各箱水产品产量单位：，其频率分布直方图如图 根据频率分布直方图，下列说法正确的是A. 新网箱产量的方差的估计值高于旧网箱产量的方差的估计值B. 新网箱产量中位数的估计值高于旧网箱产量中位数的估计值C. 新网箱产量平均数的估计值高于旧网箱产量平均数的估计值D. 新网箱频率最高组的总产量的估计值接近旧网箱频率最高组总产量估计值的两倍13.（5分）设一组样本的统计数据为：，，…，，其中，，，…，已知该样本的统计数据的平均数为，方差为，设函数，则下列说法正确的是A. 设，则，，…，，的平均数为B. 设，则，，…，的方差为C. 当时，函数有最小值D. …三 、填空题（本大题共5小题，共25分）14.（5分）已知某校甲、乙、丙三个年级的学生志愿者人数分别为，，现采用分层抽样的方法从中抽取名同学去某敬老院参加献爱心活动．应从甲乙丙三个年级的学生志愿者中分别抽取________人.15.（5分）要从1000个（其中白球有50个）球中抽取100个进行抽样分析，如果用分层抽样的方法对球进行抽样，则应抽取白球的个数是____．16.（5分）某校有500名学生，其中O型血的有200人，A型血的人有125人，B型血的有125人，AB型血的有50人，为了研究血型与色弱的关系，要从中抽取一个20人的样本，按分层抽样，O型血应抽取的人数为____人．17.（5分）某单位普通职工和行政人员共人．为了解他们在“学习强国”平台上的学习情况，现用分层抽样的方法从所有职员中抽取容量为的样本．已知从普通职工中抽取的人数为，则该单位行政人员的人数为___.18.（5分）已知某样本数据频率分布直方图共有个小长方形，若中间一个小长方形的面积等于其他个小长方形面积和的，则中间一个小长方形的面积为______．四 、解答题（本大题共5小题，共60分）19.（12分）如图所示的是甲、乙两人在一次射击比赛中中靶的情况击中靶中心的圆面为环，靶中各数字表示该数字所在圆环被击中时所得的环数，每人射击了次. 请用列表法将甲、乙两人的射击成绩统计出来； 请用学过的统计知识，对甲、乙两人这次的射击情况进行比较.20.（12分）某校从高一新生开学摸底测试成绩中随机抽取人的成绩，按成绩分组并得各组频数如下单位：分：，；，；，；，；，；，．成绩分组频数频率频率组距                  合计   列出频率分布表； 画出频率分布直方图； 估计本次考试成绩的中位数精确到．21.（12分）莞草编织的莞席曾是东莞人的骄傲，早在诗经就有”上莞下箅，乃安斯寝“近年来莞草生长环境恶劣，为保护东莞草编织这一非物质文化遗产，东莞市非遗保护中心在沙田镇设立莞草种植基地，以保障莞草的生长．某科研所为进一步改良莞草，对莞草的生长高度进行研究，在基地随机抽取了株莞草，测量其生长高度单位：，并绘制成频率分布直方图．如图所示．   Ⅰ求样本中生长高度在以上含的株数；Ⅱ由频率分布直方图估算该基地莞草株高的平均数和方差；Ⅲ现从该样本中某株高度依次是：，，，，，的莞草中任取株，求这两株高度和不少于的概率．22.（12分）某研究机构为了了解某校学生在暑假使用手机的情况，在该校随机抽取了名学生其中男、女生人数之比为：进行问卷调查．进行统计后将这名学生按男、女分为两组，再将每组学生在暑假每天使用手机的时间单位：分钟分为组，得到如图所示的频率分布直方图所抽取的学生在暑假每天使用手机的时间均不超过分钟  求出女生组频率分布直方图中的值； 求女、男生的第百分位数精确到； 求抽取的名学生中在暑假每天使用手机时间不少于分钟的学生人数．23.（12分）为了解某小区月用电量情况，通过抽样，获得了户居民月用电量单位：度，将数据按照，，，分成六组，制成了如图所示的频率分布直方图． Ⅰ求频率分布直方图中的值； Ⅱ已知该小区有户居民，估计该小区月用电量不低于度的户数，并说明理由； Ⅲ估计该小区的居民月用电量的值，并说明理由．
答案和解析1.【答案】B;【解析】解：根据题意，根据图中数据知，第一季度的数据是，，；  第二季度的数据是，，；  第三季度的数据是，，；  第四季度的数据是，，；  观察得出第二季度的数据波动性最小，所以第二季度的平均浓度指数方差最小；  故选：． 根据题意，结合表中的数据，分析表中个季度中数据的波动大小，结合方差的意义分析可得答案． 该题考查折线图的分析，涉及方差的意义，属于基础题． 2.【答案】B;【解析】解：在频率分步直方图中小长方形的面积为频率． 在的频率为，频数为， 在的频率为，频数为． 则新生婴儿的体重在内大约有 人． 故选：． 新生婴儿的体重在的分为，两部分．在频率分步直方图中小长方形的面积为频率，用长乘以宽，得到频率，用频率乘总体个数，分别得到这两个范围中的个体数．再相加可得答案． 该题考查频率分步直方图，考查频率分步直方图中小长方形的面积等于频率，考查频率，频数和样本容量之间的关系． 3.【答案】C;【解析】解：由频率分布直方图知，，， 所以中位数在内，可设为，则，解得，所以中位数是，选项错误； 最高的小矩形是所以众数是，选项错误； 计算平均数为，选项正确； 因为低于的频率为，所以不低于的频率为， 所以该校读书不低于本的人数约为人，选项错误． 故选： 根据频率分布直方图，即可求出中位数、众数、平均数，计算对应的频率和频数． 此题主要考查了利用频率分布直方图求中位数、众数、平均数，计算对应的频率和频数的应用问题，是基础题． 4.【答案】C;【解析】解：对于，由统计图可知，年我国约有万所幼儿园，故选项错误； 对于，这十年间我国学前教育毛入园率逐年增长，但是增长率不相同，故选项错误； 对于，年我国约有万所幼儿园，年我国约有万所幼儿园， 所以增长了，故选项正确； 对于，年入园率为，年入园率为， 所以增长了，故选项错误． 故选： 根据统计图中的数据信息，对四个选项逐一分析判断即可． 此题主要考查了统计图的理解和应用，解答该题的关键是正确读取统计图中的数据信息，考查了逻辑推理能力与识图能力，属于基础题． 5.【答案】C;【解析】 此题主要考查分层抽样的应用，根据比例关系是解决本题的关键，属于基础题． 由题意可求出高一、高二、高三的人数分别为：，，，即可得出该样本中的高二学生人数．  解：设该校高二共有学生人， 则，解得， 所以高一、高二、高三的人数分别为：，，， 因为， 所以样本中高二学生人数为：， 故选   6.【答案】C;【解析】解：根据频率分布直方图得； 该居民小区年龄在内的频率为 ， 所以，该年龄段的人数是 人； 所以，年龄在的频数为  故选： 根据频率和为，求出年龄在内的频率以及频数，即可求出年龄在的频数． 此题主要考查了频率分布直方图的应用问题，也考查了频率的应用问题，是基础题目． 7.【答案】B;【解析】解：根据题意可知样本中参与跑步的人数为人，所以高二级参与跑步的学生中应抽取的人数为人． 故选：． 先求得参与跑步的总人数，再乘以抽样比例，得出样本中参与跑步的人数． 这道题主要考查了分成抽样，分层抽样又称按比例抽样，是高考中常见的题型，同时考查了分析问题、解决问题的能力，属于基础题． 8.【答案】C;【解析】解：设随机变量的取值为，，，，， 则， 所以． 故选：． 先计算出平均数，然后代入方差的公式即可． 该题考查了平均数和方差的计算，属于基础题． 9.【答案】AD;【解析】 此题主要考查了条形统计图和折线统计图信息的获取，考查了读图能力和分析能力，属于基础题. 根据我国高中阶段在校生数条形图和毛入学率的折线图，进行逐项分析，即可得出答案.  解：根据条形图和折线图可知，年我国高中阶段的在校生数和毛入学率比建国初期大幅度提高，故正确； 根据条形图可知，我国高中阶段的在校生数在年后有下降趋势，故错误； 根据条形图和折线图可知，年我国高中阶段在校生数达到了最高峰，而我国高中阶段的毛入学率还在上升趋势，故错误； 据图分析，年高中阶段在校生数比年下降了  ，而毛入学率提高了，故正确. 故选 10.【答案】BCD;【解析】 此题主要考查数字特征， 考查处理前后数据的平均数、众数、百分位数及方差之间的关系，属于基础题. 解：因为，，，的众数、平均数、方差、第百分位数分别是，，，， 所以数据，，的众数、平均数、方差、第百分位数分别是，，，， 所以，，，，的众数、平均数、方差、第百分位数分别是，，，，   11.【答案】BD;【解析】解：对于，设数据，，…，的平均数为，则数据，，…，的平均数为，两组数据的平均数不相同，错误； 对于，设数据，，…，的方差为，则数据，，…，的方差也为，两组数据的方差相同，正确； 对于，设数据，，…，的中位数是，则数据，，…，的中位数是，两组数据的中位数不相同，错误； 对于，因为…，，为非零常数，所以数据的极差为，数据的极差为， 所以两组样本数据的极差相同，正确． 故选： 直接利用平均数、中位数、方差、极差的定义判断即可． 此题主要考查了命题真假的判断问题，也考查了平均数、中位数、方差、极差的定义应用问题，是基础题． 12.【答案】BCD;【解析】 此题主要考查命题真假的判断，考查频率分布直方图的性质等基础知识，考查运算求解能力，是基础题． 利用频率分布直方图的性质结合选项进行计算，得出正确结论．  解：由新旧网箱养殖方法产量的频率分布直方图，知：  在中，新网箱产量的方差的估计值低于旧网箱产量的方差的估计值，故错误；  在中，新网箱产量中位数的估计值为，高于旧网箱产量中位数的估计值，故正确； 在中，新网箱产量平均数的估计值高于旧网箱产量平均数的估计值，故正确；  在中，旧网箱频率最高组总产量估计值为， 新网箱频率最高组的总产量的估计值为， 所以新网箱频率最高组的总产量的估计值接近旧网箱频率最高组总产量估计值的两倍，故正确．  故选： 13.【答案】AC;【解析】解：对于，，，，的平均数， ，，，的平均数为： ，故正确； 对于，，，，的方差， ，，…，的平均数为： ……， 方差为：，故错误； 对于，， ，， ， 当时，函数有最小值，故正确； 对于，由上知，，，， …，故错误． 故选： 、选项直接计算平均数和方差即可判断；选项先化简得到，再结合得到，即判断；的最小值即可判断选项． 本题考命题真假的判断，考查平均数、方差的定义和性质等基础知识，考查运算求解能力，是中档题． 14.【答案】；；;【解析】 此题主要考查了分层抽样法，属于基础题. 利用分层抽样的性质能求出应从甲、乙、丙三个年级的学生志愿意者中分别抽取得人，人，人．  解：由已知得甲、乙、丙三个年级的学生志愿者人数之比为：：：：，由于采用分层抽样的方法从中抽取名同学，应从甲、乙、丙三个年级的学生志愿意者中分别抽取得人，人，人． 故答案为；； 15.【答案】5;【解析】解：白球所占的比例为501000=120，采用按颜色分层抽样的方法抽取100个，应抽取白球的个数为5个． 故答案为：5． 16.【答案】8;【解析】解：根据题意知用分层抽样方法抽样． ∵20500=250， ∴O型血应抽取的人数为200×250=8，故O型血抽8人． 故答案为：8． 17.【答案】;【解析】 此题主要考查分层抽样的应用，属于基础题.  解：由题意得，该单位行政人员和普通职工人数之比为， 根矩分层抽样的规则，该单位行政人员的人数为 故答案为 18.【答案】0.2;【解析】解：设频率直方图中间的面积为，则，所以． 故答案为：． 有频率分布直方图的总面积为总概率，可以求出． 该题考查频率直方图，属于基础题． 19.【答案】解：（1）甲、乙两人的射击成绩统计表如下：环数678910甲命中次数00222乙命中次数01032（2）=×（8×2+9×2+10×2）=9（环）， =×（7×1+9×3+10×2）=9（环）， S2甲=×[（8-9）2×2+（9-9）2×2+（10-9）2×2]=， S2乙=×[（7-9）2+（9-9）2×3+（10-9）2×2]=1， 因为甲=，S2甲＜S2乙， 所以甲与乙的平均成绩相同，但甲的发挥比乙稳定．;【解析】 由已知数据能作出甲、乙两人的射击成绩统计表． 分别求出甲、乙两人这次的射击的平均数和方差，得到甲与乙的平均成绩相同，但甲的发挥比乙稳定． 此题主要考查统计表、平均数、方差等基础知识，考查运算求解能力，是基础题． 20.【答案】解：（1）由题意列出频率分布表如下：成绩分组频数频率频率/组距[40，50）40.040.004[50，60）60.060.006[60，70）200.20.02[70，80）300.30.03[80，90）240.240.024[90，100]160.160.016合计10010.1（2）画出频率分布直方图，如下：  （3）由频率分布直方图得： [40，70）的频率为：0.04+0.06+0.2=0.3，[70，80）的频率为0.3， ∴估计本次考试成绩的中位数为： 70+≈76.7．;【解析】 由题意能列出频率分布表．  由频率分布表能画出频率分布直方图．  由频率分布直方图得：的频率为：，的频率为，由此能估计本次考试成绩的中位数． 该题考查频率分布表频率分布直方图、考试成绩的中位数的求法，考查频率分布直方图的性质等基础知识，考查运算求解能力，考查数形结合思想，是基础题． 21.【答案】本题满分为分 解：Ⅰ由频率分布直方图可知，样本中生长高度在以上含的频率为 ， 所以样本中生长高度在以上含的株数为：；分 Ⅱ由频率分布直方图可估计： 分 分 该基地莞草株高的平均数为，方差为；分 Ⅲ设两株高度和不少于的事件为， 记高度依次为，，，，，， 分别为，，，，，，则两株高度和共有种结果，如下：   其中包含了共个结果， 所以分 故这两株高度和不少于的概率为分;【解析】 Ⅰ由频率分布直方图可求样本中生长高度在以上含的频率，进而可求株数；  Ⅱ频率分布直方图各个小矩形的面积乘底边中点的横坐标之和可求平均数，利用方差公式即可得解；  Ⅲ设两株高度和不少于的事件为，记高度依次为，，，，，，分别为，，，，，，则两株高度和共有种结果，分析可得包含了个结果，即可计算得解． 该题考查频率分直方图的应用，考查概率的求法，考查数据处理论证能力、运算求解能力，考查数形结合思想、函数与方程思想，属于中档题． 22.【答案】解：， 设女、男生的第百分位数分别为，， 由图知： ，， 女生的第百分位数分别约为分钟； ， ，男生的第百分位数分别为分钟． 名学生中男、女生人数分别为，， 即抽取的名学生中每天使用手机时间不少于分钟的学生人数为;【解析】此题主要考查由频率分布直方图求频率，频数、中位数，属于基础题． 根据频率之和为列出方程求解即可； 第百分位数即中位数，根据由频率直方图求中位数的方法求解即可； 由频率直方图计算每天使用手机时间不少于分钟的学生的频率，即可得出学生人数．   23.【答案】解：（Ⅰ）由频率分布直方图可得：（0.0024+0.0036+0.0060+x+0.0024+0.0012）×50=1， 解得：x=0.0044． （Ⅱ）由频率分布直方图可得，100户居民7月用电量不低于200度的频率为（0.0044+0.0024+0.0012）×50=0.4， 由此可以估计该小区有1000户居民7月用电量不低于200度的户数为1000×0.4=400． （Ⅲ）由频率分布直方图可得，7月用电量低于250度的频率为0.82，7月用电量低于300度的频率为0.94， 所以85%分位数一定位于区间（250.300）内， 由250+50×=262.5． 由此估计该小区85%的居民7月用电量约为262.5度．;【解析】 Ⅰ由概率统计相关知识，各组频率和为，列出方程求出的值；  Ⅱ由频率分布直方图可得户居民月用电量不低于度的频率为，由此得解．  Ⅲ由频率分布直方图可得分位数一定位于区间内，由此得解． 该题考查了利用频率分布直方图求频率、频数的应用问题，是基础题目．