初中2.9 有理数的乘方完美版ppt课件

这是一份初中2.9 有理数的乘方完美版ppt课件，共31页。PPT课件主要包含了学习目标，情境导入，探究新知，随堂练习，课堂小结等内容，欢迎下载使用。
1.在现实背景中，理解有理数乘方的意义2.理解并掌握有理数的乘方、幂、底数、指数的概 念及意义3.能够正确进行有理数的乘方运算.
国际象棋起源于印度。棋盘上共有8行8列构成64个格子。
传说国王要奖赏国际象棋的发明者：他的大宰相西萨·班·达伊尔，国王问他有什么要求，这位聪明的大宰相的胃口并不是太大，他跪在国王面前说：
“皇帝陛下，请在棋盘的第1个格子里放上1颗麦粒，在棋盘的第2个格子里放上2颗麦粒，在棋盘的第3个格子里放上4颗麦粒，在棋盘的第4个格子里放上8颗麦粒，以此类推，每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍，直到第64个格子。请都赏给你的仆人吧！”
没过一会儿，他的粮管就来报告了，“国王，不对呀！我们的整个国家的粮库的粮食都才能摆到30格，如果满足他这个要求，我们国家要全国不吃不喝种两千多年哪！”
国王听了很不以为然，说：“爱卿，你的要求并不多呀，我一定满足你的要求！”
纸对折1次后变成了几层？
按照刚才折纸的规律，将一张足够长的纸连续20次，应该是多少层？
请同学猜想：对折10次有几层？怎样列算式表示？
2×2×2×2×2×2×2×2×2×2
一直对折下去，你们知道会发生什么吗？
一张厚度为0.1毫米的纸张折叠27次后，它的高度相当于1.5个珠穆朗玛峰！继续折叠30次后有10万多米高，有12个珠穆朗玛峰高！
这样写起来很麻烦，既浪费时间又浪费空间，有没有一种简单的记法呢？
珠穆朗玛峰，海拔高度是8844米．如果我们把一张足够大的厚度为0．1毫米的纸，连续对折30次，那么它的厚度就能超过珠穆朗玛峰。
2×2×2……2×2×2×2×2×2×2
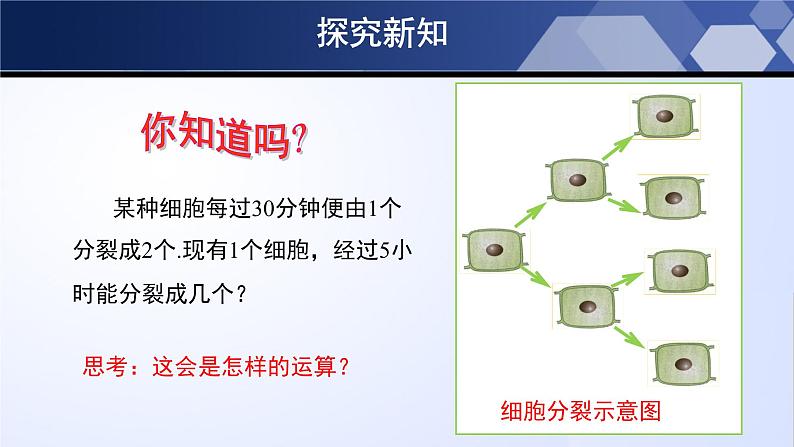
某种细胞每过30分钟便由1个分裂成2个.现有1个细胞，经过5小时能分裂成几个？
思考：这会是怎样的运算？
思考：分裂5小时会有多少个细胞？
这个细胞分裂一次可得多少个细胞?分裂两次呢?分裂三次呢?四次呢？ 那么, 3小时共分裂了多少次?有多少个细胞？
一次得：2个；两次得：2×2个;三次得：2×2×2个;四次得：2×2×2×2个；六次得：2×2×2×2×2×2个.
请比较细胞分裂四次后的个数式子：2×2×2×2和细胞分裂六次后的个数式子： 2×2×2×2×2×2.
1. 这两个式子有什么相同点?
它们都是乘法; 并且它们各自的因数都相同.
2. 同学们想一想：这样的运算能像平方、立方 那样简写吗？
这样的运算我们可以像平方和立方那样简写：
2×2×2×2 =
2×2×2×2×2 =
2×2×2×2×2×2×2×2×2×2 =
如果把2换成3呢？
3×3×3×3 =
3×3×3×3×3 =
3×3×3×3×3×3×3×3×3×3 =
你发现这种简写的规律了吗？
求n个相同因数的积的运算，叫做乘方.
读法：an可以读作a的n次方，也可读作a的n次幂.
注意：1.一个数可以看作这个数本身的一次方，例如8就是81，通常指数为1时省略不写.2.一般地，在an中，a取任意有理数，n取正整数。3.乘方是一种运算，幂是乘方运算的结果。
练一练：(-2)4 ， -24，它们一样吗？说说它们的意义与读法.
思考:它们的底数分别是什么?相同么?
(-2)4的底数是-2 ，-24的底数是2，它们的底数是不相同的．
(-2)4 =(-2)×(-2)×(-2)×(-2) =16，表示4个(-2)相乘，读作 ．
-24 =-2×2×2×2=-16 ，表示4个2相乘的相反数，读作 或 ．
“2的4次方的相反数”
练一练：计算下列各数 ， 它们一样吗？说说它们的意义.
思考:它们的底数分别是什么?
它们的底数是不相同的．
，表示2的平方再除以3．
的底数是 ， 的底数是2．
例：计算：
注意：1.当底数是负数或分数时一定要用括号把底数括起来.2.先根据乘方的性质，确定符号，再根据乘方的意义，把乘方转化为乘法来计算．注意当底数是带分数时，需先化为假分数，当底数是小数时，需先化为分数，再进行乘方计算．
想一想 ：一个正数的乘方，结果一定是正数吗？
结论：正数的任何次幂都是正数.
一个负数的乘方，结果一定是负数吗？
负数的偶次幂是正数；负数的奇次幂是负数.
0的乘方，结果会是什么样？
0的任意正整数次幂都是0.
正数的任何次幂都是正数.负数的偶次幂是正数；负数的奇次幂是负数.0的任何正整数次幂都是0.
乘方运算的步骤：先确定符号、再求值.
乘方运算的符号法则：
1.a3表示（　　） A. 3a　　 B. a＋a＋a　　C. a·a·a D. a＋32.（－3）4表示（　　）A.4乘（－3）的积 B.4个（－3）连乘的积C.3个（－4）连乘的积 D.4个（－3）相加的和
3.对于－32与（－3）2，下列说法正确的是（　　）A.读法相同，底数不同，结果不同B.读法不同，底数不同，结果相同C.读法相同，底数相同，结果不同D.读法不同，底数不同，结果不同
4.（－3）2计算的结果是（　　） A.－6 B.6 C.－9 D.9
5.下列各数中，最小的是（　　） A.－3 B.|－2| C.（－3）2 D.2×103
6.下列各组数中,互为相反数的是( ) A.-23与(-2)3 B.｜-22｜与-(-22) C.-34与(-3)4 D.102与210
7.下列等式成立的是（　　） A.（－3）2＝－32 B.－23＝（－2）3 C. 23＝（－2）3 D.32＝－32
8.（-2）10的底数是___，指数是 ____，读作______________9. x m 表示____个___相乘,指数是___,底数是__,读作__________ .
10.立方等于它本身的数是 .
(3)-0.24; (4)-(-4)3.
原式=-（2×2×2×2）
解：原式=10×10×10×10
原式=-（0.2×0.2×0.2×0.2）
原式=-（-4）×（-4）×（-4）
11.计算： (1)104; (2)-24;
12.计算：(1)-(-3)3；
解：(1)-(-3)3＝-(-33)＝33＝3×3×3＝27.
13.已知| b-2 |与 (a+1)2 互为相反数，求ab 的值.
∴ b=2, a= -1，
求n个相同因数的积的运算叫做乘方，乘方的结果叫做幂.
2. 1的任何次幂是1；0的任何正整数次幂都是0.
1.正数的任何正整数次幂都是正数；负数的奇次幂是负数，负数的偶次幂是正数.