初中数学北师大版七年级上册2.1 有理数试讲课课件ppt

这是一份初中数学北师大版七年级上册2.1 有理数试讲课课件ppt，共42页。PPT课件主要包含了本章知识架构，知识专题，五相反数，六绝对值，七有理数的大小比较，科学记数法，科学记数法的概念，a与n的取法，绝对值，相反数等内容，欢迎下载使用。

一．正数与负数：正数：大于 0 的数叫做正数．正数前面的“＋”可以省略．负数： “－”号的数叫做负数．负数前面的“－”不可以省略． 正负号具有相反的意义，在任何一个数前面加上“－”就变成这个数的相反数
二．有理数的概念（1）整数和分数统称为有理数．（2）整数包括正整数、0、负整数．（3）分数包括正分数、负分数，（4）分数都可以化为有限小数或无限循环小数的形式，有限小数或无限循环小数都可以化为分数的形式.所以有限小数和无限循环小数都属于分数．
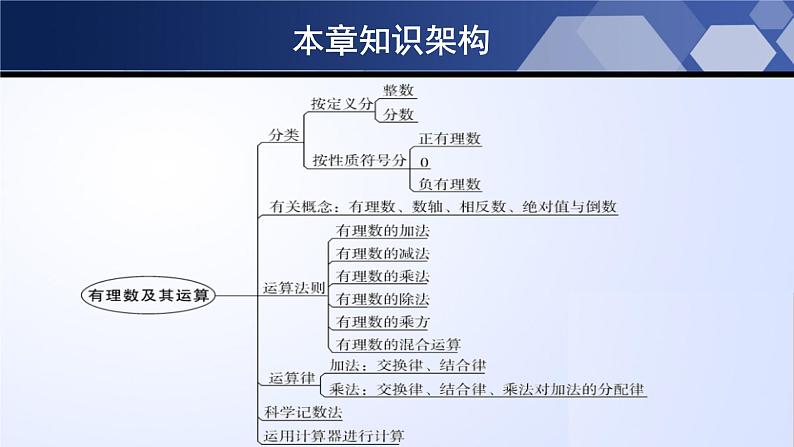
三．有理数的分类按有理数的定义进行分类：按有理数的性质符号进行分类：
注意： （1）正整数是指既是正数，又是整数的数；负整数是指既是负数，又是整数的数；正分数是指既是正数， 又是分数的数；负分数是指既是负数，又是分数的数． （2）非负数是指正数和 0；非正数是指负数和 0；非负整数是非负的整数，即正整数和 0． （3） 既不是正数，也不是负数，但它是整数． （4）任何有限小数和无限循环小数都是分数，都是有理数．
（5）无限不循环小数不能转化成分数，不是有理数，是我们以后要学的无理数，例如圆周率 π、 、自然对数的底数 e、0.1010010001……（每2个1之间0的个数逐次加1）等都不是有理数，而是无理数．因此分数只是小数的一部分，分数和小数是两个不同的概念．（6）把一些数放在一起，就组成了一个集合，简称数集．所有的有理数组成的数集叫做有理数集；所有的整数组成的数集叫做整数集；所有的正数组成的数集叫做正数集；所有的负数组成的数集叫做负数集．
四.数轴1.规定了原点、正方向和单位长度的直线叫做数轴，如图所示．2.数轴的三要素：原点、正方向和单位长度．三者缺一不可．3.数轴的画法：（1）画一条水平直线；（2）在这条直线上的适当位置取一点作为原点；
（3）规定直线 上向右的方向为正方向，用箭头表示出来；（4）选取适当的长度作为单位长度，用细短线画出，并对应地标注各数，同时要注意同一数轴的单位长度要一致．4.任何一个有理数都可以用数轴上的一个点来表示．0用原点表示，正有理数用原点右边的点表示（在数轴上要画出实心的小圆点），负有理数用原点左边的点表示．数轴上两个点表示的数，右边的总比左边的大．正数大于 0，负数小于 0，正数大于负数．
1. 定义：如果两个数只有符号不同，那么称其中一个数为另一个数的相反数．特别地，0的相反数是0．要点诠释：（1）“只”字是说仅仅是符号不同，其它部分完全相同．（2）“0的相反数是0”是相反数定义的一部分，不能漏掉．（3）相反数是成对出现的，单独一个数不能说是相反数．（4）求一个数的相反数，只要在它的前面添上“-”号即可．
2.性质：（1）互为相反数的两数的点分别位于原点的两旁，且与原点的距离相等（这两个点关于原点对称）．（2）互为相反数的两数和为0．
1．定义：在数轴上，一个数所对应的点与原点的距离叫做这个数的绝对值，例如+2的绝对值等于2，记作|+2|=2；-3的绝对值等于3，记作|-3|=3．2．性质：（1）0除外，绝对值为一正数的数有两个，它们互为相反数．（2）互为相反数的两个数（0除外）的绝对值相等.（3）绝对值具有非负性，即任何一个数的绝对值总是正数或0
要点诠释：（1）绝对值的代数意义：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．即对于任何有理数a都有：
（2）绝对值的几何意义：一个数的绝对值就是表示这个数的点到原点的距离，离原点的距离越远，绝对值越大；离原点的距离越近，绝对值越小．（3）一个有理数是由符号和绝对值两个方面来确定的．
1．数轴法：在数轴上表示出这两个有理数，左边的数总比右边的数小． 如：a与b在数轴上的位置如图所示，则a＜b．
2．法则比较法：两个数比较大小，按数的性质符号分类，情况如下：
要点诠释：利用绝对值比较两个负数的大小的步骤：（1）分别计算两数的绝对值；（2）比较绝对值的大小：（3）判定两数的大小．
在a×10n形式中，n的值是原数整数位数减1，a则是将原数保留一位整数得来的．
一个大于10的数可以表示成a×10n的形式，其中1≤a<10，n是正整数，这种记数方法叫做科学记数法．
九. 有理数的加法(1)有理数加法法则：①同号两数________，取相同的符号，并把______相加. ②异号两数相加，绝对值相等时和为____；绝对值不等时，取绝对值_______的数的符号，并用较大的绝对值______较小的绝对值. ③一个数同0相加，仍得这个数. (2)相关运算律加法交换律：a+b=b+a；加法结合律：(a+b)+c=a+(b+c).
十. 有理数的减法(1)有理数减法法则：减去一个数，等于加上这个数的________，即a-b=a+(-b). (2)方法指引：①在进行减法运算时，首先弄清减数的符号； ②将有理数转化为加法时，要同时改变两个符号：一是_______(减号变加号)； 二是减数的__________(减数变相反数). 【注意】：在有理数减法运算时，被减数与减数的位置不能随意交换，因为减法没有交换律.
十一. 有理数的加减混合运算(1)有理数加减混合运算的方法：有理数的加减混合运算可以统一成_______运算. (2)方法指引：①在一个式子里，有加法也有减法，根据有理数减法法则，把减法都转化成_______，并写成省略括号的和的形式. ②转化成省略括号的代数和的形式，就可以应用加法的运算律，使计算简化.
十二. 有理数的乘法(1)有理数乘法法则：两数相乘，同号得_____，异号得_____，并把绝对值_______. (2)任何数同零相乘，积仍为_____. (3)多个有理数相乘的法则：①几个不等于0的数相乘，积的符号由________的个数决定，当负因数有______个时，积为负；当负因数有_______个时，积为正. ②几个数相乘，有一个因数为0，积就为______.
(4)方法指引：①运用乘法法则，先确定_______，再把绝对值_________. ②多个因数相乘，看0因数和积的符号当先，这样做使运算既准确又简单.
十三. 有理数的除法有理数的除法运算，通常有两种方法：(1)利用有理数的除法法则，即：两个有理数相除，同号得_____，异号得____，并把绝对值_______；0除以任何非0的数都得0. 注意：0不能做除数. (2)将有理数的除法运算转化为乘法运算：除以一个数等于乘这个数的_______.
十四. 有理数的乘方(1)有理数乘方的定义：求n个相同因数积的运算，叫做________. 乘方的结果叫做_____，在an中，a叫做______，n叫做_____. an读作__________. (将an看作是a的n次方的结果时，也可以读作a的n次幂. )(2)乘方的法则：正数的任何次幂都是______；负数的奇次幂是______，负数的偶次幂是______；0的任何正整数次幂都是_____. (3)方法指引：有理数的乘方运算与有理数的加减乘除运算一样，首先要确定幂的符号，然后再计算幂的绝对值.
十五. 有理数的混合运算(1)有理数混合运算顺序：先算________，再算_____，最后算______；同级运算，应按_________的顺序进行计算；如果有括号，要先算____________. (2)进行有理数的混合运算时，注意各个运算律的运用，使运算过程得到简化.
1.下列各组量中，具有相反意义的量是（ ）A．节约汽油 10 升和浪费粮食 10kg B．向东走 8km 和向北走8km C．收入 300 元和支出 100 元 D．身高 180cm 和身高 90cm
2.我国古代《九章算术》中注有“今两算得失相反，要令正负以名之”．意思是现在有两数，若其意义相反，则分别叫做正数与负数．如果你向东走 10 步记作＋10 步，那么向西走 9 步 记 作 （ ）A．＋9 步 B．－9 步 C．＋1 步 D．－19 步
3.（1）如果零上 5℃记作＋5℃，那么零下 3℃记作 ．（2）某仓库运进面粉 7.5t 记作＋7.5t，那么运出面粉 3.8t 应记作 ．（3） 东、西为两个相反方向，如果－4m 表示一个物体向西运动 4m，那么物体向东运动 2m 应记作（）A．＋2m B．－2m C．＋4m D．－4m（4）如果某蓄水池的水位比标准水位高 2 米记作＋2 米，那么比标准水位低 0.8 米应记作 ；恰好等于标准水位应记作 ．
4.把下列各数填入相应的集合中：
5．下列各图中，是数轴的是（ ）
6．指出数轴上 A、B、C、D、E 各点分别表示的有理数，并用“＜”将它们连接起来．
7. 如图，表示互为相反数的两个数的点是________．
8. 判断下列说法是否正确： （1）－3是相反数 ； （2）+3是相反数； （3）3是－3的相反数； （4）－3与+3互为相反数.
10. 化简下列各数： －(－68) ，－(＋0.75)， , －(＋3.8) 68，－0.75， ，－3.8
9. 如果a=- a，那么表示a 的点在数轴上的什么位置？ 原点
11. 写出下列各式的值，并回答问题．
12.请用科学记数法表示下表中的数据：
13. 计算：（1）-23+（-3）×｜-4｜-（-4）2+（-2）；
解：（1）原式=-8+（-3）×4-16-2 =-8-12-16-2 =-38.
（2）-14-［2-（-3）2］÷ ；
（3） ×（-36）；
（4）（-1）3-［2-（-3）2］÷ .
（4）原式=（-1）-（2-9）×（-2） =（-1）-（-7）×（-2） =（-1）-14 =-15.
13.滴滴打车是一种网上约车方式，更方便人们出行，小明国庆节第一天下午营运全是在安庆某大道南北走向的公路上进行的，向北记作“+”，向南记作“-”. 他这天下午行车情况如下：（单位：千米，每次行车都有乘客）-10，+5，-2，+8，-6，-4，+7， +8. 请回答：
（1）小明将最后一名乘客送到目的地时，小明在下午出车的出发地的什么方向？距下午出车的出发地多远？
解：（1）-10+5-2+8-6-4+7+8=6（千米）.答：小明在下午出车的出发地的正北方向，距下午出车的出发地6千米.
（2）若小明的出租车每千米耗油0.06升，每升汽油6.5元，这八次出车共耗油费多少元？
（2）（10+5+2+8+6+4+7+8）×0.06×6.5=50×0.06×6.5=19.5（元）.答：这八次出车共耗油费19.5元.