初中数学华师大版八年级上册1 平方根教案设计

11.1平方根与立方根

——平方根

三维教学目标

知识与技能：

1、了解算术平方根的概念、会用根号表示一个数的平方根与算术平方根.

2、进一步明确平方与开平方是互为逆运算.

3、会利用开方运算求某些非负数的平方根与算术平方根.

4、会用计算器求某些非负数的算术平方根.

过程与方法：

1、让学生经历概念形成过程，提高学生学习兴趣.

2、.鼓励学生进行探索和交流，培养他们的创新意识和合作精神.

情感态度与价值观：

1、培养学生在学习中互相帮助、相互合作的团队精神.

2、培养学生认真仔细的学习态度，以及思维的严谨性.

教学重点：会利用开方运算求某些非负数的平方根与算术平方根.

教学难点：如何理解是非负数及被开方数是非负数.

课堂导入

知识回顾：1、什么是平方根？求36、1.44、的平方根.

2、  任何数都有平方根吗？为什么？

教学过程

一、探索归纳

填一填：

1、  正数有_____个平方根，它们互为相反数.

2、  ___和____都是64 的平方根

3、  ____和____都是1.44的平方根

4、  0的算术平方根呢？

概括：

1、算术平方根定义以及表示.

我们把正数a的正的平方根叫做a的算术平方根，0的算术平方根为0.

记作： 读作：根号a.

所以64的算术平方根表示为

2、平方根的表示法

正数a的平方根表示为

所以64的平方根表示为

3、开平方运算

二、举例应用

例2将下列各数开平方：

（1）49；       （2）

解（1） 因为7＝49，所以＝7，因此49的平方根为±7；

（2）因为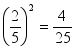，所以，因此的平方根为±.

如果遇到一些比较大的数求它的算术平方根，可借助计算器.

例3用计算器求下列各数的算术平方根：

（1） 529；（2）44.81（精确到0.01）．

解（1） 在计算器上依次键入

，

显示结果为23，所以529的算术平方根为

＝23．

（2） 在计算器上依次键入

，

显示结果为      ，要求精确到0.01，所以44.81的算术平方根为

        ．

三、课堂练习

1、见课本练习（略）.

2、的算术平方根是______.

（-4）2的算术平方根是        .

3、 若有意义，则a能取的最小整数为______.

4、 用计算器计算：

（1）；（2）；（3）（精确到0.01）．

5、 下列说法正确吗?为什么?如果不正确，那么请你写出正确答案．

（1） 0.09的算术平方根是0.3；

（2）＝±5

答案：

2、2，4  3、0  4、（略） 5、（1）正确；（2）、不正确，＝5．

四、课堂小结：

1、算术平方根与平方根的意义与表示方法.

2、式子中被开方数应该满足的条件.

3、用计算器求一个非负数的算术平方根的按键顺序.

课堂作业

1、的平方根是______.

2、（-2）2的算术平方根是        .

3、求下列各数的平方根及算术平方根

4、若，求x+y的值.

答案：

1、±3 因为=9，9的平方根为±3.

2、2因为（-2）2 =4，所以4的算术平方根为2.

3、  ， ；，，

4、根据题意得：x+1=0

              x-y=0   ,解得x=-1,y=-1  x+y=-2

教学反思

1、对平方根、算术平方根的意义与表示方法不理解

学生把误认为a的平方根;或者把误认为a的算术平方根，为避免出现错误，要彻底弄清楚：正数a有两个平方根，表示为.有一个算术平方根表示为

2、审题不认真忽略“”

在求一个数的平方根时，如果这个数本身带有根号，会忽略这个数本身的根号而出错.