华师大版八年级上册11.2 实数教案

11.2 实数

三维教学目标

知识与技能：

1、  了解无理数、实数的概念，以及实数的两种分类。

2、  能判断一个数是有理数还是无理数。

3、  了解实数与数轴上的点一一对应的关系。

过程与方法：

1、  通过亲身探索，认识到实数和数轴上的点一一对应的关系，体会数形结合的思想。

2、  鼓励从定义和性质两方面对实数进行分类，体会分类讨论的思想方法。

情感态度与价值观：

1、  让学生经历数系扩张的过程，进一步体验数系的发展源于实际，又作用于实际的辩证关系。培养学生的数感与估数能力。

2、  培养学生严谨治学的学习态度，刻苦学习的精神。

教学重点：无理数、实数的概念及实数的分类；实数与数轴上的点一一对应的关系。

教学难点：对实数与数轴上的点一一对应关系的理解。

课堂导入

首先我们来进行一个数学活动。

1.做一做：、(1)用计算器求；(2)利用平方关系验算所得结果。

这里，我们用计算器求得=1.414213562，再用计算器计算1.414213562的平方，结果是1.999999999，并不是2，只是接近2。这就是说，我们求得的的值，只是一个近似值。

2.如果用计算机计算，结果如何呢？

阅读课本第15页的计算结果，在数学上已经证明，没有一个有理数的平方等于2，也就是说，不是有理数．那么，是怎样的数呢？

教学过程

一、探索归纳

1、回顾有理数的概念

（1）有理数的分类。

（2）随意写几个数，将其化为小数，看一看结果，由此可得什么结论。

2、无理数、实数概念

无限不循环小数叫做无理数．有理数和无理数统称为实数。

计算结果是无限不循环小数，所以不是有理数．类似地，、圆周率π等也都不是有理数，它们都是无限不循环小数。

3、实数的分类

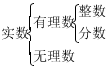
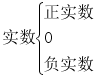
（1）从定义分                   （2）从正、负分

二、试一试

1、按计算器显示的结果，想象在数轴上的位置。

2、在数轴上，你能找到表示的点吗？

三、反思提高

1、将所有有理数都标在数轴上，那么数轴被填满了吗？

2、若再将所有无理数都标在数轴上，数轴被填满了吗？

归纳：数轴上的任一点表示的数，不是有理数，就是无理数。数学上可以说明，数轴上的任一点必定表示一个实数；反过来，每一个实数也都可以用数轴上的点来表示。换句话说，实数与数轴上的点一一对应。

四、举例应用

例1、在下列各数中，哪些是有理数？哪些是无理数？

3.14,,π,,,,,,0.20200200020002...

解：有理数是：

无理数是：

五、课堂练习

1.下列各数中：

－，，3.14159,π,,－,0,0.,,,2.121122111222…

其中有理数有___________________________________.

无理数有_______________________________________.

2.判断正误

（1）有理数包括整数、分数和零（    ）

（2）无理数都是开方开不尽的数（    ）

3、在数轴上找到表示的点。

六、课堂小结

1、什么是无理数？实数？

2、实数如何分类？

3、实数与数轴上的点有什么关系？

课堂作业

1、下列各数，哪些是有理数，哪些是无理数？

2、下列各数哪些是正实数、负有理数？

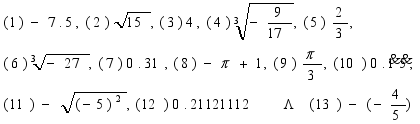
3、  在数轴上找到表示的点。

答案：

1、有理数有：；无理数有：

2、正实数有（2），（3），（5），（7），（9），（10），（12）（13）

负有理数有（1），（6），（11）

3、在数轴上做一长为2个单位长度，宽为1个单位长度的长方形，它的对角线的长为，然后借助圆规，以原点为圆心，长为半径作弧，找到这一点。

教学反思

1、“无理数是无限小数”和“无限小数是无理数”这两种说法对吗？

第一种说法正确，第二种说法错误。因为无理数是指无限的不循环小数，所以无理数是无限小数；但无限小数中有循环和不循环小数两种，其中一种是有理数，所以无限小数是无理数错误。

2、有理数和无理数的区别

有理数总可以用有限小数和循环小数来表示，无理数只能用无限不循环小数来表示。