人教版初中数学七年级上册 1.1 正数和负数 课件+教案+导学案+分层练习（含教师+学生版）

这是一份人教版初中数学七年级上册 1.1 正数和负数 课件+教案+导学案+分层作业（含教师学生版），文件包含11正数和负数教学课件pptx、11正数和负数分层作业解析版docx、11正数和负数教学设计docx、11正数和负数导学案docx、11正数和负数分层作业原卷版docx等5份课件配套教学资源，其中PPT共39页， 欢迎下载使用。

1.1 正数和负数
人教版数学七年级上册
1.了解正数与负数是从实际需要中产生的.（抽象能力）2.理解正数、负数及0的意义，掌握正数、负数的表示方法.（抽象能力）3.会用正数、负数表示具有相反意义的量.（抽象能力、应用意识）
中国最北端位于黑龙江省的漠河县.下图为漠河县4月16日~4月22日的天气预报：
图中这些数字表示什么意义？
（1）天气预报北京冬季里某一天的温度为－3℃ ~ 3℃，它的确切含义是什么？这一天北京的温差是多少？（2）某年，我国花生产量比上一年增长1.8%，油菜籽产量比上一年增长－2.7%.“增长－2.7%”表示什么意思？
自学任务一：阅读本章引言中的几个问题，说一说，这些数都表示什么实际意义？
（3）夏新同学通过捡、卖废品，既保护了环境，又积攒了零花钱．下表是他某个月的部分收支情况： 收支情况表 ____年___月
自学任务一：阅读本章引言中的几个问题，说一说，这些数都表示什么实际意义？
本章引言中，表示温度、产量增长率、收支情况时，既要用到数3，1.8%，3.5等，还要用到数-3，-2.7%，-4.5，-1.2等，它们实际意义分别是：零下3摄氏度，减少2.7%，支出4.5元，亏空1.2元.
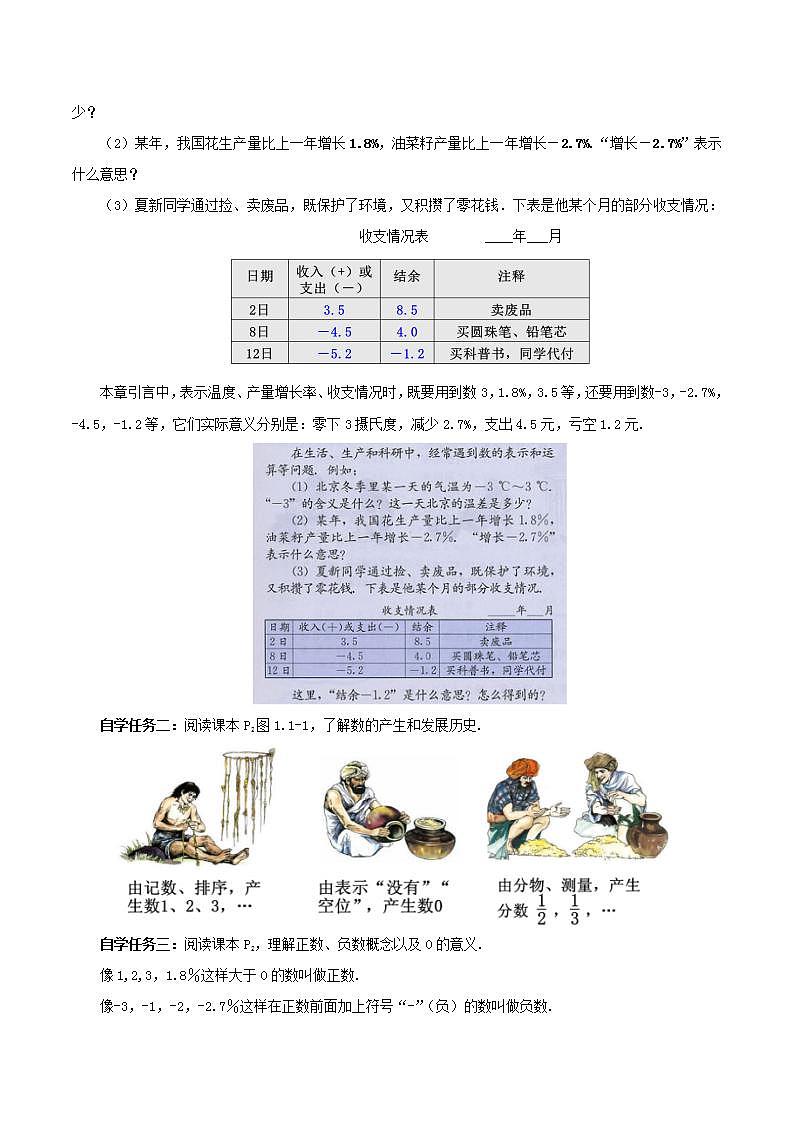
自学任务二：阅读课本P2图1.1-1，了解数的产生和发展历史.
自学任务三：阅读课本P2，理解正数、负数概念以及0的意义.
像1,2,3，1.8％这样大于0的数叫做正数.
像-3，-1，-2，-2.7％这样在正数前面加上符号“-”（负）的数叫做负数.
一个数前面的“+”“-”号叫做它的符号.有时，我们为了明确表达意义，在正数前面也加上“+”（正）号，如+3，+1.8％，+0.5，….不过一般情况下我们省略“+”不写.
小于0的数叫做负数.
0既不是正数，也不是负数.
自学任务四：根据实际生活的需要，人们引进了负数，观察下面两幅图说说这些负数表示的实际意义.再结合你的生活实际，试举例身边的负数.
电梯楼层按钮
商场楼层示意图
 
正数
负数
【点睛】这类题型解题要点是认清负数的特征：从定义中我们发现负数的前面必须有负号“-”；同时还要特别注意从正负数的定义可知：“0既不是正数，也不是负数”.
 
 
 
 
-21，-π，-35%
A
例2.（1）一个月内，小明体重增加2kg，小华体重减少1kg，小强体重无变化，写出他们这个月的体重增长值；
解：规定体重增加记为“+”，体重减少记为“-”，则：这个月小明体重增长2kg，小华体重增长-1kg，小强体重增长0kg.
解：规定增长记为“+”，减少记为“-”，则：六个国家2001年商品出口总额的增长率：美国 -6.4%， 德国 1.3%，法国 -2.4%， 英国 -3.5%，意大利 0.2%， 中国 7.5%.
（2）某年下列国家的商品进出口总额比上年的变化情况是： 美国减少6.4%， 德国增长1.3%，法国减少2.4%， 英国减少3.5%，意大利增长0.2%，中国增长7.5%.写出这些国家2001年商品进出口总额的增长率.
相反
你能从例题的解答过程中，总结一下如何用正数、负数表示实际问题中具有相反意义的量吗？
①先找出表示具有相反意义的量的词.如“增加”和“减少”、“零上”和“零下”、“上升”和“下降”、“盈利”和“亏损”、“收入”和“支出”等.②选定一方用正数表示，那么另一方就用负数表示.
从上面的例题中看到增长－1就是减少1，那么增长－6.4%是什么意思呢？什么情况下增长率是0？减少－1又是什么意思呢？
深入思考
1.2010年我国全年平均降水量比上年增加108.7mm，2009年比上年减少81.5mm，2008年比上年增加53.5mm. 用正数和负数表示这三年我国全年平均降水量比上年的增长量.
解：这三年我国全年平均降水量比上年的增长量分别是： 2010年 108.7mm，2009年 -81.5mm，2008年 53.5mm.
2.如果把一个物体向右移动1m记作移动+1m，那么这个物体又移动了-1m是什么意思？如何描述这时物体的位置？
解：这个物体又移动了-1m表示物体又向左移动1m；此时物体回到原来的位置.
海平面
珠穆朗玛峰
吐鲁番盆地
高度看作0
探究一：下图是吐鲁番盆地的示意图，你能用语言表述它与海平面的高度关系吗？它的含义是什么？
记为+8844.43米
记为－155米
探究二：下面的正数和负数的含义是什么？你能再举一些用正数、负数表示数量的实际例子吗？
探究三：0只表示没有吗?
1.空罐中的金币数量;2.温度中的0℃;3.海平面的高度;4.标准水位;5.身高比较的基准; ……
0是正负数的分界点.它不再简简单单的只表示没有，它具有丰富的意义，如
0可以用来表示基准，一般地，高于基准的量用正数表示，低于基准的量用负数表示
例3.下列说法正确的是（ ）A.0是负数B.不是正数的数一定是负数C.海拔0m表示没有高度D.非负数是指正数和0
D
1.下列语句正确的是 （ ） A.0℃表示没有温度 B.0表示什么也没有 C.0是非正数 D.0既可以看作是正数又可以看作是负数
2.你能举出实际生活中0表示的实际意义吗？请举两例.

解：答案不唯一，如：收支为0元，表示收入和支出平衡；水位变化0m，表示水位不上升也不下降.
C
例4.一次体育课，老师对七年级女生进行了仰卧起坐的测试，以做36个为标准，超过的次数用正数表示，不足的次数用负数表示，第一小组8人的成绩如下：2，－3，4，0，1，－1，－5，0.（1）这8名同学实际各做了多少次仰卧起坐？ （2）这个小组的达标率是多少？
解：（1）这8名同学实际做仰卧起坐的次数分别为：38，33，40，36，37，35，31，36．（2）因为有5人达标，所以达标率为：5÷8=0.625=62.5%．
某个体儿童服装店老板以每件32元的价格购进30件连衣裙，针对不同的顾客，30件连衣裙的售价不完全相同，若以40元为标准价，将超过的钱数记为正，不足的钱数记为负，则记录结果如表所示：
（1）在销售过程中①最低售价为每件______元;②最高获利为每件______元.（2）该服装店在售完这30件连衣裙后，赚了多少钱？
解：①40-6=34元，②40+5-32=13元，（2）5×4+2×9+1×3﹣2×5﹣3×4﹣6×5+（40﹣32）×30＝229元，答：该服装店在售完这30件连衣裙后，赚了229元．
例5.某饮料公司生产的一种瓶装饮料，外包装上印有“(600±30)mL”的字样，那么(600±30)mL表示什么意思?质检员抽查了5瓶该产品，饮料的容量分别为603mL，611mL，588mL，568mL，628mL，抽查的5瓶饮料的容量是否合格?
解:(600±30)mL表示合格产品的容量范围在(600-30)mL到(600+30)mL之间(即在570mL~630mL之间),因此抽查的5瓶饮料中容量为603mL，611mL，588 mL，628mL的合格,容量为568mL的不合格.
1.如图是加工零件的尺寸要求，现有下列直径尺寸的产品(图中长度单位:mm) ,其中不合格的是( )A.φ45.02 B.φ44.9C.φ44.98 D.φ45.01
B
2.一商品的标准价格是120元，但随着季节的变化，商品的价格可浮动±10%. (1)±10%的含义是__________________________________;(2)该商品的最高价格是________，最低价格是_______.
最多比标准价格上涨10%或下降10%
108元
132元
例6.【数形结合思想】如果一个物体向左移动5m,记作-5m,那么:(1)这个物体第二次移动+5m是什么意思?这时物体离它两次移动前的位置有多远?(2)如果第二次移动+7m,那么是什么意思?这时物体在它两次移动前的什么位置?
解:(1)表示这个物体第二次向右移动5m,这时物体回到了出发点，即在它两次移动前的位置上.(2)表示这个物体第二次向右移动71m,这时物体在出发点的右边2m处，即在它两次移动前的右边2m处.
例6.【数形结合思想】如果一个物体向左移动5m,记作-5m,那么:(1)这个物体第二次移动+5m是什么意思?这时物体离它两次移动前的位置有多远?(2)如果第二次移动+7m,那么是什么意思?这时物体在它两次移动前的什么位置?
文具店、书店和玩具店依次位状元成才于一条东西走向的大街上，文具店在书店西边20m处，玩具店在书店东边100m处.小明从书店沿街向东走了40m，接着又向东走了-60m，此时小明在( )A.文具店 B.玩具店C.文具店西边40m处 D.玩具店西边60m处
A
例7.观察下面一列数:-1，+2，-3，+4，-5，+6，-7，+8，-9，… (1)这一列数中的第101个数是_____，第1000个数是________.(2)在前1000个数中,正数和负数分别有多少个?(3)2033是否在这列数中?若在，说出它是第几个数;若不在,请说明理由.
-101
+1000
例7.观察下面一列数:-1，+2，-3，+4，-5，+6，-7，+8，-9，… (1)这一列数中的第101个数是_____，第1000个数是________.(2)在前1000个数中,正数和负数分别有多少个?(3)2033是否在这列数中?若在，说出它是第几个数;若不在,请说明理由.
-101
+1000
(2)因为正数和负数是间隔交替出现，所以前1000个数中，正数和负数各有500个.(3)2033不在这列数中.理由:根据这列数的排列规律，奇数前面的符号都是“-”号,所以2033不在这列数中.
将一串数按下列规律排列,回答后面的问题:(1)在A处的数是正数还是负数?(2)负数排在A，B，C，D中的什么位置?(3)第2043个数是正数还是负数?排在对应于A，B，C，D中的什么位置?
解:(1)正数.(2)负数排在B，D的位置.(3)因为2043÷4=510……3，所以第2043个数是负数，排在对应于D的位置.
概念
正数和负数表示实际问题中的具有相反意义的量.
在具体的问题情境中明了正数和负数代表的实际意义.
正数和负数的定义
0的意义不仅是表示“没有”，还是正数和负数的分界.
正数、0、负数