

2023年浙江省台州市中考数学试卷(含答案解析)
展开2023年浙江省台州市中考数学试卷
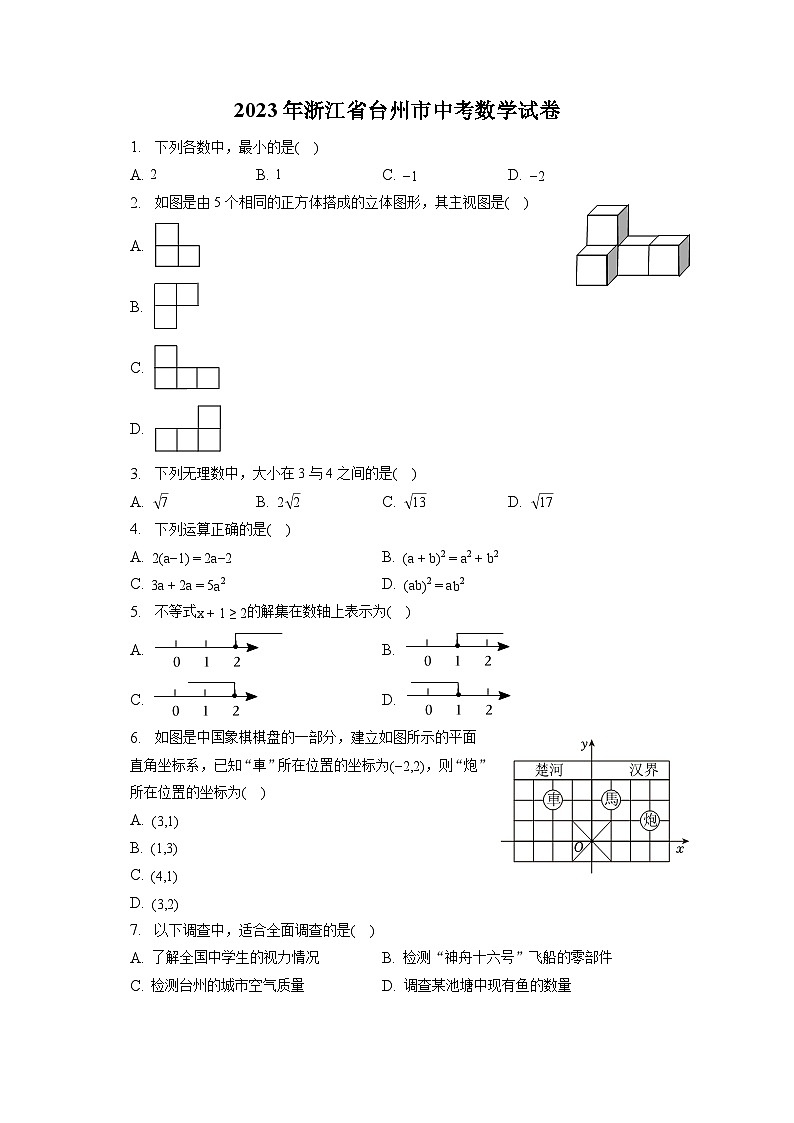
1. 下列各数中,最小的是( )
A. 2 B. 1 C. −1 D. −2
2. 如图是由5个相同的正方体搭成的立体图形,其主视图是( )
A.
B.
C.
D.
3. 下列无理数中,大小在3与4之间的是( )
A. 7 B. 2 2 C. 13 D. 17
4. 下列运算正确的是( )
A. 2(a−1)=2a−2 B. (a+b)2=a2+b2
C. 3a+2a=5a2 D. (ab)2=ab2
5. 不等式x+1≥2的解集在数轴上表示为( )
A. B.
C. D.
6. 如图是中国象棋棋盘的一部分,建立如图所示的平面直角坐标系,已知“車”所在位置的坐标为(−2,2),则“炮”所在位置的坐标为( )
A. (3,1)
B. (1,3)
C. (4,1)
D. (3,2)
7. 以下调查中,适合全面调查的是( )
A. 了解全国中学生的视力情况 B. 检测“神舟十六号”飞船的零部件
C. 检测台州的城市空气质量 D. 调查某池塘中现有鱼的数量
8. 如图,⊙O的圆心O与正方形的中心重合,已知⊙O的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点距离的最小值为( )
A. 2
B. 2
C. 4+2 2
D. 4−2 2
9. 如图,锐角三角形ABC中,AB=AC,点D,E分别在边AB,AC上,连接BE,CD.下列命题中,假命题是( )
A. 若CD=BE,则∠DCB=∠EBC
B. 若∠DCB=∠EBC,则CD=BE
C. 若BD=CE,则∠DCB=∠EBC
D. 若∠DCB=∠EBC,则BD=CE
10. 抛物线y=ax2−a(a≠0)与直线y=kx交于A(x1,y1),B(x2,y2)两点,若x1+x2<0,则直线y=ax+k一定经过( )
A. 第一、二象限 B. 第二、三象限 C. 第三、四象限 D. 第一、四象限
11. 因式分解:x2−3x=______ .
12. 一个不透明的口袋中有5个除颜色外完全相同的小球,其中2个红球,3个白球.随机摸出一个小球,摸出红球的概率是______ .
13. 用一张等宽的纸条折成如图所示的图案,若∠1=20∘,则∠2的度数为______ .
14. 如图,矩形ABCD中,AB=4,AD=6.在边AD上取一点E,使BE=BC,过点C作CF⊥BE,垂足为点F,则BF的长为______ .
15. 3月12日植树节期间,某校环保小卫士组织植树活动.第一组植树12棵;第二组比第一组多6人,植树36棵;结果两组平均每人植树的棵数相等,则第一组有______ 人.
16. 如图,点C,D在线段AB上(点C在点A,D之间),分别以AD,BC为边向同侧作等边三角形ADE与等边三角形CBF,边长分别为a,b,CF与DE交于点H,延长AE,BF交于点G,AG长为c.
(1)若四边形EHFG的周长与△CDH的周长相等,则a,b,c之间的等量关系为______ ;
(2)若四边形EHFG的面积与△CDH的面积相等,则a,b,c之间的等量关系为______ .
17. 计算:22+|−3|− 25.
18. 解方程组:x+y=72x−y=2.
19. 教室里的投影仪投影时,可以把投影光线CA,CB及在黑板上的投影图象高度AB抽象成如图所示的△ABC,∠BAC=90∘,黑板上投影图象的高度AB=120cm,CB与AB的夹角∠B=33.7∘,求AC的长.(结果精确到1cm.参考数据:sin33.7∘≈0.55,cos33.7∘≈0.83,tan33.7∘≈0.67)
20. 科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm3)的反比例函数,当密度计悬浮在密度为1g/cm3的水中时,h=20cm.
(1)求h关于ρ的函数解析式;
(2)当密度计悬浮在另一种液体中时,h=25cm,求该液体的密度ρ.
21. 如图,四边形ABCD中,AD//BC,∠A=∠C,BD为对角线.
(1)证明:四边形ABCD是平行四边形;
(2)已知AD>AB,请用无刻度的直尺和圆规作菱形BEDF,顶点E,F分别在边BC,AD上(保留作图痕迹,不要求写作法).
22. 为了改进几何教学,张老师选择A,B两班进行教学实验研究,在实验班B实施新的教学方法,在控制班A采用原来的教学方法.在实验开始前,进行一次几何能力测试(前测,总分25分),经过一段时间的教学后,再用难度、题型、总分相同的试卷进行测试(后测),得到前测和后测数据并整理成表1和表2.
表1:前测数据
测试分数x
0
28
9
9
3
1
实验班B
25
10
8
2
1
表2:后测数据
测试分数x
0
14
16
12
6
2
实验班B
6
8
11
18
3
(1)A,B两班的学生人数分别是多少?
(2)请选择一种适当的统计量,分析比较A,B两班的后测数据.
(3)通过分析前测、后测数据,请对张老师的教学实验效果进行评价.
23. 我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置.如图,AB是⊙O的直径,直线l是⊙O的切线,B为切点.P,Q是圆上两点(不与点A重合,且在直径AB的同侧),分别作射线AP,AQ交直线l于点C,点D.
(1)如图1,当AB=6,BP长为π时,求BC的长;
(2)如图2,当AQAB=34,BP=PQ时,求BCCD的值;
(3)如图3,当sin∠BAQ= 64,BC=CD时,连接BP,PQ,直接写出PQBP的值.
24. 【问题背景】“刻漏”是我国古代的一种利用水流计时的工具.综合实践小组准备用甲、乙两个透明的竖直放置的容器和一根带节流阀(控制水的流速大小)的软管制作简易计时装置.
【实验操作】综合实践小组设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始放水后每隔10min观察一次甲容器中的水面高度,获得的数据如表:
流水时间t/min
0
10
20
30
40
水面高度h/cm(观察值)
30
29
28.1
27
25.8
任务1:分别计算表中每隔10min水面高度观察值的变化量.
【建立模型】小组讨论发现:“t=0,h=30”是初始状态下的准确数据,水面高度值的变化不均匀,但可以用一次函数近似地刻画水面高度h与流水时间t的关系.
任务2:利用t=0时,h=30;t=10时,h=29这两组数据求水面高度h与流水时间t的函数解析式;
【反思优化】经检验,发现有两组表中观察值不满足任务2中求出的函数解析式,存在偏差,小组决定优化函数解析式,减少偏差.通过查阅资料后知道:t为表中数据时,根据解析式求出所对应的函数值,计算这些函数值与对应h的观察值之差的平方和,记为w;w越小,偏差越小.
任务3:(1)计算任务2得到的函数解析式的w值;
(2)请确定经过(0,30)的一次函数解析式,使得w的值最小;
【设计刻度】得到优化的函数解析式后,综合实践小组决定在甲容器外壁设计刻度,通过刻度直接读取时间.
任务4:请你简要写出时间刻度的设计方案.
答案和解析
1.【答案】D
【解析】解:∵|−1|=1,|−2|=2,1<2,
∴−1>−2,
则2>1>−1>−2,
那么最小的数为:−2,
故选:D.
正数>0>负数,两个负数比较大小,绝对值大的反而小;据此进行判断即可.
本题考查有理数的大小比较,此为基础且重要知识点,必须熟练掌握.
2.【答案】C
【解析】解:从正面看该组合体,其主视图是.
故选:C.
根据主视图的意义,从正面看该组合体所得到的图形进行判断即可.
本题考查简单组合体的三视图,理解视图的意义,掌握三视图的画法是正确判断的前提.
3.【答案】C
【解析】解:∵4<7<8<9<13<16<17,
∴ 4< 7< 8< 9< 13< 16< 17,
即2< 7<2 2<3< 13<4< 17,
那么 13在3和4之间,
故选:C.
一个正数越大,其算术平方根越大;据此进行无理数的估算进行判断即可.
本题考查无理数的估算,此为基础且重要知识点,必须熟练掌握.
4.【答案】A
【解析】解:A.2(a−1)
=2a−2×1
=2a−2,
则A符合题意;
B.(a+b)2=a2+2ab+b2,
则B不符合题意;
C.3a+2a
=(3+2)a
=5a,
则C不符合题意;
D.(ab)2=a2b2,
则D不符合题意;
故选:A.
根据去括号法则,完全平方公式,合并同类项法则,积的乘方法则将各项计算后进行判断即可.
本题考查整式的运算,其相关运算法则是基础且重要知识点,必须熟练掌握.
5.【答案】B
【解析】解:x+1≥2,
解得:x≥1,
在数轴上表示,如图所示:
.
故选:B.
直接解一元一次不等式,再将解集在数轴上表示即可.
此题主要考查了解一元一次不等式,正确解不等式是解题关键.
6.【答案】A
【解析】解:如图所示:“炮”所在位置的坐标为:(3,1).
故选:A.
直接利用“車”位于点(−2,2),得出原点的位置,进而得出答案.
此题主要考查了坐标确定位置,正确得出原点的位置是解题关键.
7.【答案】B
【解析】解:A.了解全国中学生的视力情况,适合抽样调查,故本选项不合题意;
B.检测“神舟十六号”飞船的零部件,适合普查,故本选项符合题意;
C.检测台州的城市空气质量,适合抽样调查,故本选项不合题意;
D.调查某池塘中现有鱼的数量,适合抽样调查,故本选项不合题意.
故选:B.
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
8.【答案】D
【解析】解:如图,点B为⊙O上一点,点D为正方形上一点,连接BD,OC,OA,AB,
由三角形三边关系可得,OB−OD
∴当O、A、B三点共线时,圆上任意一点到正方形边上任意一点距离有最小值,最小值为OB−AB,
由题意可得,AC=4,OB=4,
∵点O为正方形的中心,
∴OA⊥OC,OA=OC,
∴△AOC为等腰直角三角形,
∴OA=AC 2=4 2=2 2,
∴圆上任意一点到正方形边上任意一点距离的最小值为OB−AB=4−2 2.
故选:D.
如图,由三角形三边关系分析可得当O、A、B三点共线时,圆上任意一点到正方形边上任意一点距离有最小值,最小值为OB−AB,以此即可求解.
本题主要考查正方形的性质、利用三角形三边关系求最值问题,利用三角形三边关系分析得出当O、A、B三点共线时,圆上任意一点到正方形边上任意一点距离有最小值是解题关键.
9.【答案】A
【解析】解:∵AB=AC,
∴∠ABC=∠ACB,
∵BC=BC,∠DCB=∠EBC,
∴△DCB≌△EBC(ASA),
∴CD=BE,故选项B是真命题,不符合题意;
BD=CE,故选项D是真命题,不符合题意;
∵BC=BC,∠ABC=∠ACB,BD=CE,
∴△DCB≌△EBC(SAS),
∴∠DCB=∠EBC,故选项C是真命题,不符合题意;
不能证明CD=BE时,∠DCB=∠EBC,故选项A是假命题,符合题意;
故选:A.
由AB=AC,得∠ABC=∠ACB,而BC=BC,∠DCB=∠EBC,可得△DCB≌△EBC(ASA),故CD=BE,判断选项B是真命题;BD=CE,判断选项D是真命题;根据BC=BC,∠ABC=∠ACB,BD=CE,得△DCB≌△EBC(SAS),有∠DCB=∠EBC,判断选项C是真命题;不能证明CD=BE时,∠DCB=∠EBC,可判断选项A是假命题.
本题考查命题与定理,涉及全等三角形的判定与性质,等腰三角形性质及应用,解题的关键是掌握全等三角形判定定理.
10.【答案】D
【解析】解:∵抛物线y=ax2−a(a≠0)与直线y=kx交于A(x1,y1),B(x2,y2)两点,
∴kx=ax2−a,
∴ax2−kx−a=0,
∴x1+x2=ka,
∴ka<0,
当a>0,k<0时,直线y=ax+k经过第一、三、四象限,
当a<0,k>0时,直线y=ax+k经过第一、二、四象限,
综上,直线y=ax+k一定经过一、四象限.
故选:D.
根据已知条件可得出ax2−kx−a=0,再利用根与系数的关系,分情况讨论即可.
本题考查了二次函数与系数的关系,解题的关键是熟练掌握根与系数的关系.
11.【答案】x(x−3)
【解析】解:原式=x⋅x−x⋅3
=x(x−3),
故答案为:x(x−3).
提取公因式x即可.
本题考查提公因式法因式分解,此为基础且重要知识点,必须熟练掌握.
12.【答案】25
【解析】解:∵一个口袋里有5个除颜色外完全相同的小球,其中2个红球,3个白球,
∴摸到红球的概率是25.
故答案为:25.
利用红球的个数÷球的总个数可得红球的概率.
此题主要考查了概率公式,关键是掌握概率=所求情况数与总情况数之比.
13.【答案】140∘
【解析】解:如图,标注三角形的三个顶点A、B、C.
∠2=∠BAC=180∘−∠ABC−∠ACB.
∵图案是由一张等宽的纸条折成的,
∴AB=AC,
∴∠ABC=∠ACB.
又∵纸条的长边平行,
∴∠ABC=∠1=20∘,
∴∠2=∠BAC=180∘−2∠ABC=180∘−2∠1=180∘−2×20∘=140∘.
故答案为:140∘.
利用平行线的性质和各角之间的关系即可求解.
本题比较简单,主要考查了平行线的性质的运用.
14.【答案】2 5
【解析】解:∵四边形ABCD是矩形,
∴AD//BC,∠A=90∘,
∴∠AEB=∠FBC,
∵CF⊥BE,
∴∠CFB=90∘,
∴∠CFB=∠A,
在△ABE和△FCB中,
∠A=∠CFB∠AEB=∠FBCBE=CB,
∴△ABE≌△FCB(AAS),
∴FC=AB=4,
∵四边形ABCD是矩形,
∴BC=AD=6,
在Rt△FCB中,由勾股定理得BF= BC2−FC2= 62−42=2 5,
故答案为:2 5.
根据矩形的性质可得出∠AEB=∠FBC,结合已知BE=BC,利用AAS证得△ABE和△FCB全等,得出FC=AB=4,再根据矩形的性质得到BC=AD=6,从而在Rt△FCB中利用勾股定理求出BF的长.
本题考查了矩形的性质,三角形全等的性质与判定,勾股定理,熟知矩形的对边平行且相等,四个角都是直角.
15.【答案】3
【解析】解:设第一组有x人,则第二组有(x+6)人,依题意有:
12x=36x+6,
解得x=3,
经检验,x=3是原方程的解.
故第一组有3人.
故答案为:3.
可设第一组有x人,则第二组有(x+6)人,根据两组平均每人植树的棵数相等,列出方程计算即可求解.
本题考查了应用类问题,关键是根据两组平均每人植树的棵数相等找到等量关系.
16.【答案】5a+5b=7ca2+b2=c2
【解析】解:(1)∵△ADE和△CBF是等边三角形,
∴∠A=∠ADE=∠B=∠BCF=60∘,
∴△CDH和△ABG是等边三角形,DE//BG,CF//AG,
∴四边形EHFG是平行四边形,AB=AG=BG=c,CH=DH=CD=AD+BC−AB=a+b−c,
∴EG=AG−AE=c−a,GF=BG−BF=c−b,
∵四边形EHFG的周长与△CDH的周长相等,
∴2[(c−a)+(c−b)]=3(a+b−c),
整理得:5a+5b=7c,
故答案为:5a+5b=7c;
(2)∵S四边形EHFG=S△ABG−S△BCF−S△ADE+S△CDH,四边形EHFG的面积与△CDH的面积相等,
∴S△ABG−S△BCF−S△ADE+S△CDH=S△CDH,
∴S△ABG=S△BCF+S△ADE,
∵△ABG,△ADE和△CBF是等边三角形,
∴ 34c2= 34a2+ 34b2,
∴c2=a2+b2,
故答案为:a2+b2=c2.
(1)由△ADE和△CBF是等边三角形,可得△CDH和△ABG是等边三角形,DE//BG,CF//AG,即知EG=AG−AE=c−a,GF=BG−BF=c−b,根据四边形EHFG的周长与△CDH的周长相等,有2[(c−a)+(c−b)]=3(a+b−c),故5a+5b=7c;
(2)由S四边形EHFG=S△ABG−S△BCF−S△ADE+S△CDH,四边形EHFG的面积与△CDH的面积相等,可得S△ABG=S△BCF+S△ADE,即 34c2= 34a2+ 34b2,从而可得a2+b2=c2.
本题考查等边三角形的性质及应用,解题的关键是用含a,b,c的代数式表示相关线段的长度.
17.【答案】解:22+|−3|− 25
=4+3− 52
=4+3−5
=7−5
=2.
【解析】根据有理数的乘方,绝对值的性质,算术平方根进行计算即可.
本题考查实数的运算,实数的相关运算法则是基础且重要知识点,必须熟练掌握.
18.【答案】解:{x+y=7①2x−y=2②,
①+②得3x=9,
解得x=3,
把x=3代入①,得3+y=7,
解得y=4,
∴方程组的解是x=3y=4.
【解析】利用加减消元法求解即可.
本题主要考查解二元一次方程组,解答的关键是熟练掌握解二元一次方程组的方法.
19.【答案】解:在Rt△ABC中,AB=120cm,∠BAC=90∘,∠B=33.7∘,
∴tanB=ACAB,
∴AC=AB⋅tan33.7∘≈120×0.67=80.4≈80(cm),
∴AC的长约为80cm.
【解析】在Rt△ABC中,利用锐角三角函数的定义进行计算,即可解答.
本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.
20.【答案】解:(1)设h关于ρ的函数解析式为h=kρ,
把ρ=1,h=20代入解析式,得k=1×20=20,
∴h关于ρ的函数解析式为h=20ρ;
(2)把h=25代入h=20ρ,得25=20ρ,
解得:ρ=0.8,
答:该液体的密度ρ为0.8g/cm3.
【解析】(1)设h关于ρ的函数解析式为h=kρ,把ρ=1,h=20代入解析式,解方程即可得到结论;
(2)把h=25代入h=20ρ,求得ρ=0.8,于是得到结论.
本题考查了反比例函数的应用,正确地求出反比例函数的解析式是解题的关键.
21.【答案】(1)证明:∵AD//BC,
∴∠ADB=∠CBD,∠A=∠C,
∴180∘−(∠ADB+∠A)=180∘−(∠CBD+∠C),
即∠ABD=∠CDB,
∴AB//CD,
∴四边形ABCD是平行四边形;
(2)解:如图,四边形BEDF就是所求作的菱形.
【解析】(1)证明AB//CD,可得结论;
(2)桌线段BD的垂直平分线交AD与点F交BC与点E即可.
本题考查作图-复杂作图,平行四边形的判定和性质,菱形的判定等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
22.【答案】解:(1)A班的人数:28+9+9+3+1=50(人),
B班的人数:25+10+8+2+1=46(人),
答:A,B两班的学生人数分别是50人,46人.
(2)x−A=14×2.5+16×7.5+12×12.5+6×17.5+2×22.550=9.1,
x−B=6×2.5+8×7.5+11×12.5+18×17.5+3×22.546≈12.9,
从平均数看,B班成绩好于A班成绩.
从中位数看,A班中位数在5
(3)前测结果中:
x−A=28×2.5+9×7.5+9×12.5+3×17.5+1×22.550=6.5,
x−B=25×2.5+10×7.5+8×12.5+2×17.5+1×22.546≈6.4,
从平均数看,两班成绩较前测都有上升,但实验班提升得更明显,因此张老师新的教学方法效果较好.
从中位数看,两班前测中位数均在0
【解析】(1)将表格中A、B班各等级人数分别相加即可得出答案;
(2)分别计算出A、B班级成绩的平均数,再从平均数、中位数和百分率方面求解即可;
(3)计算出前测A、B班级成绩的平均数,再与后测的平均数、中位数及百分率分析求解即可.
本题主要考查统计量的选择,解题的关键是掌握加权平均数、中位数的定义和意义.
23.【答案】解:(1)如图,连接OP,
设∠BOP的度数为n∘,
∵AB=6,BP长为π,
∴nπ×3180=π,
∴n=60,即∠BOP=60∘,
∴∠BAP=30∘,
∵直线l是⊙O的切线,
∴∠ABC=90∘,
∴BC=AB 3=2 3;
(2)如图,连接BQ,过点C作CF⊥AD于点F,
∵AB为⊙O直径,
∴∠BQA=90∘,
∴cos∠BAQ=AQAB=34,
∵BP=PQ,
∴∠BAC=∠DAC,
∵CF⊥AD,AB⊥BC,
∴CF=BC,
∵∠BAQ+∠ADB=90∘,∠FCD+∠ADB=90∘,
∴∠FCD=∠BAQ,
∴cos∠FCD=cos∠BAQ=34,
∴CFCD=34,
∴BCCD=34;
(3)如图,连接BQ,
∵AB⊥BC,BQ⊥AD,
∴∠ABQ=90∘−∠QBD=∠ADC,
∵∠ABQ=∠APQ,
∴∠APQ=∠ADC,
∵∠PAQ=∠DAC,
∴△APQ∽△ADC,
∴PQCD=APAD①,
∵∠ABC=90∘=∠APB,∠BAC=∠PAB,
∴△APB∽△ABC,
∴BPBC=APAB②,
由BC=CD,将①②两式相除得:
PQBP=ABAD,
∵cos∠BAQ=ABAD= 104,
∴PQBP= 104.
【解析】(1)连接OP,设∠BOP的度数为n,可得nπ×3180=π,n=60,即∠BOP=60∘,故∠BAP=30∘,而直线l是⊙O的切线,有∠ABC=90∘,从而BC=AB 3=2 3;
(2)连接BQ,过点C作CF⊥AD于点F,求出cos∠BAQ=AQAB=34,由BP=PQ,得∠BAC=∠DAC,有CF=BC,证明∠FCD=∠BAQ,即得CFCD=34,故BCCD=34;
(3)连接BQ,证明△APQ∽△ADC,得PQCD=APAD①,证明△APB∽△ABC,得 BPBC=APAB②,由BC=CD,将①②两式相除得:PQBP=ABAD,故PQBP= 64.
本题考查圆的综合应用,涉及相似三角形的判定与性质,锐角三角函数,圆的切线等知识,解题的关键是熟练掌握圆的相关性质及应用.
24.【答案】解:任务1:
变化量分别为:29−30=−1(cm);28.1−29=−0.9(cm);27−28.1=−1.1(cm);25.8−27=−1.2(cm),
∴每隔10min水面高度观察值的变化量为:−1,−0.9,−1.1,−1.2.
任务2:
设水面高度h与流水时间t的函数解析式为h=kt+b,
∵t=0时,h=30;t=10时,h=29;
∴b=3010k+b=29,
解得:k=−0.1b=30,
∴水面高度h与流水时间t的函数解析式为h=−0.1t+30;
任务3:
(1)w=(30−30)²+(29−29)2+(28−28.1)2+(27−27)2+(26−25.8)2
=0.05.
(2)w=(10k+30−30)2+(10k+30−29)2+(10k+30−28.1)2+(10k+30−27)2+(10k+30−25.8)2
=3000(k+0.102)2−0.038,
∴当k=−0.102时,w的最小值为0.038.
任务4:
在容器外壁每隔1.02cm标记一次刻度,这样水面每降低一个刻度,就代表时间经过了10分钟.
【解析】任务1:依表计算即可;
任务2:根据待定系法确定关系式即可;
任务3:(1)根据题意计算即可;(2)设h=kt+30,代入w计算化简,利用二次函数性质求w的最小值即可;
任务4:按照上一问题中的结论设计即可.
本题考查了一次函数的应用,充分理解题意是解题关键.
2023年浙江省台州市中考数学试卷(含解析): 这是一份2023年浙江省台州市中考数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年浙江省台州市中考数学试卷(含解析): 这是一份2023年浙江省台州市中考数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022年浙江省台州市中考数学试卷解析版: 这是一份2022年浙江省台州市中考数学试卷解析版,共29页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












