初中数学华师大版八年级上册第13章 全等三角形13.1 命题、定理与证明1 命题精品课件ppt

这是一份初中数学华师大版八年级上册第13章 全等三角形13.1 命题、定理与证明1 命题精品课件ppt，共60页。PPT课件主要包含了怎样证明这个结论呢，①②③，角平分线等内容，欢迎下载使用。

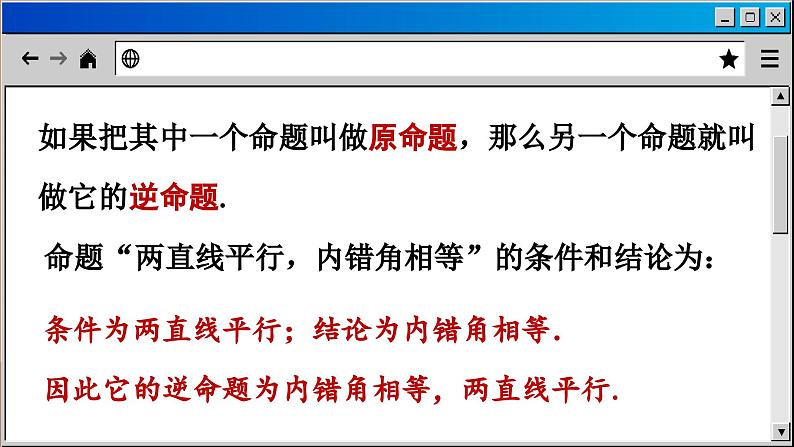
13.5 逆命题与逆定理
1.互逆命题与互逆定理
1. 理解互逆命题、互逆定理的概念，能写出一个命题的逆命题并能判定其真假；(重点)2. 能用学过的知识证明一个定理的逆命题是真命题还是假命题.(难点)
1. 什么叫命题？2. 命题由几部分组成，一般可以写成什么样的形式？3. 命题有真命题和假命题之分.
表示判断的语句叫做命题.
由条件和结论两部分组成.
可以写成“如果……，那么……”的形式.
说出下列命题的条件和结论：1. 两直线平行，内错角相等；2. 内错角相等，两直线平行；
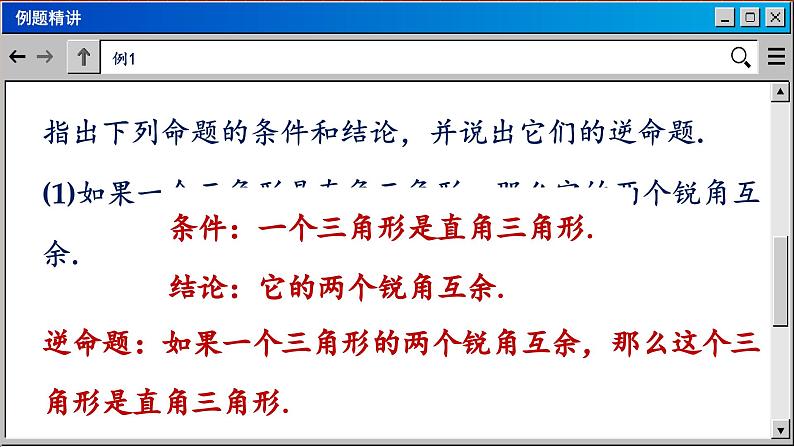
指出下列命题的条件和结论，并说出它们的逆命题.(1)如果一个三角形是直角三角形，那么它的两个锐角互余.
(2)等边三角形的每个角都等于 60°.
（3）全等三角形的对应角相等.
（4）到一个角的两边距离相等的点，在这个角的平分线上.
（5）线段的垂直平分线上的点到这条线段的两个端点的距离相等.
每一个命题都有逆命题，只要将原命题的条件改成结论，并将结论改成条件，便可得到原命题的逆命题．但是原命题正确，它的逆命题未必正确． 例如真命题“对顶角相等”的逆命题为“相等的角是对顶角”，此命题就是假命题．
举例说明下列命题的逆命题是假命题.（1）如果一个整数的个位数字是 5 ，那么这个整数能被 5 整除.
（2）如果两个角都是直角，那么这两个角相等.
如果一个定理的逆命题也是定理，那么这两个定理叫做互逆定理，其中的一个定理叫做另一个定理的逆定理. 我们已经知道命题“两直线平行，内错角相等”和它的逆命题“内错角相等，两直线平行”都是定理，因此它们就是互逆定理．
一个假命题的逆命题可以是真命题，甚至可以是定理． 例如“相等的角是对顶角”是假命题，但它的逆命题“对顶角相等”是真命题，且是定理．
注意1：逆命题、互逆命题不一定是真命题， 但逆定理、互逆定理，一定是真命题.注意2：不是所有的定理都有逆定理.
1. 理解和掌握线段垂直平分线的定理及其逆定理，并能利用它们来进行证明或计算.(重点)2. 知道线段垂直平分线是到线段两端距离相等的点的集合.3. 了解数学和生活的紧密联系.
高 速 公 路
在某高速公路 l 的同侧，有两个工厂 A、B，为了便于两厂的工人看病，市政府计划在公路边上修建一所医院，使得两个工厂的工人都没意见，问医院的院址应选在何处？你的方案是什么?
线段垂直平分线的性质定理
如图，直线 MN 是线段 AB 的垂直平分线，P 是 MN 上任一点，连结 PA、PB. 将线段 AB 沿直线 MN 对折，你发现了什么？如何表达，并简述你的证明过程.
对折后 PA、PB 能够完全重合，PA = PB.
下面我们来证明刚才得到的结论：证明： ∵MN ⊥AB（已知），∴∠ACP =∠BCP = 90° (垂直的定义).在△ACP 和△BCP 中，∵ AC = BC，∠ACP =∠BCP，PC = PC，∴ △ACP≌△BCP (S. A. S. ).∴PA = PB (全等三角形的对应边相等).
你能用一句话来描述刚得到的结论吗？
线段垂直平分线上的点到线段两端的距离相等.
线段垂直平分线的性质定理：
几何语言叙述：∵ 点 P 在线段 AB 的垂直平分线上（或 PC⊥AB，AC = BC），∴ PA = PB.
线段垂直平分线的判定定理
这一定理描述了线段垂直平分线的性质，那么反过来会有什么结果呢？写出性质定理及其逆命题的条件和结论，你有什么发现？
一个点在线段的垂直平分线上
这个点到线段两端的距离相等
一个点到线段两端的距离相等
这个点在线段的垂直平分线上
想想看，这个逆命题是不是一个真命题？你能证明吗？
逆命题 如果一个点到线段两端的距离相等，那么这个点在线段的垂直平分线上.
已知： 如图，QA＝QB.求证： 点 Q 在线段 AB 的垂直平分线上．
分析：为了证明点 Q 在线段 AB 的垂直平分线上，可以先经过点 Q 作线段 AB 的垂线，然后证明该垂线平分线段 AB；也可以先平分线段 AB，设线段 AB 的中点为点 C，然后证明 QC 垂直于线段 AB．
你能根据分析中后一种添加辅助线的方法，写出它的证明过程吗？
证明：过点 Q 作 MN⊥AB，垂足为点 C，故∠QCA =∠QCB = 90°.
在 Rt△QCA 和 Rt△QCB 中，∵ QA = QB，QC = QC，∴ Rt△QCA≌Rt△QCB（H. L. ）.∴ AC = BC.∴ 点 Q 在线段 AB 的垂直平分线上．
定理 到线段两端距离相等的点在线段的垂直平分线上.
发现：三角形三边的垂直平分线交于一点．这一点到三角形三个顶点的距离相等．
1. 会叙述角平分线的性质及判定；（重点）2. 能利用三角形全等，证明角平分线的性质定理，理解和掌握角平分线性质定理和它的逆定理．能应用这两个性质解决一些简单的实际问题；（难点）3. 经历探索、猜想、证明的过程，进一步发展推理证明意识和能力．
在一个三角形居住区内修有一个学校 P，P 到 AB、BC、CA 三边的距离都相等，请在三角形居住区内标出学校 P 的位置，P 在何处？
角是轴对称图形吗？它的对称轴是什么？
如图，点 P 是∠AOB 的角平分线 OC 上的任意一点，且 PD⊥OA 于点 D，PE⊥OB 于点 E，将∠AOB 沿 OC 对折，你发现了什么？如何表达，并简述你的证明过程.
证明：∵ OC 平分∠AOB，P 是 OC 上一点，∴ ∠DOP =∠BOP.∵ PD⊥OA，PE⊥OB ，∴ ∠ODP =∠OEP = 90°.
在△OPD 和△OPE 中，∵ ∠DOP =∠EOP，∠ODP =∠OEP，OP = OP，∴ △OPD≌△OPE ( A. A. S. ). ∴PD＝PE.
角平分线性质定理的逆定理
这一定理描述了角平分线的性质，那么反过来会有什么结果呢？写出性质定理及其逆命题的条件和结论，你有什么发现？
这个点到这个角两边的距离相等
一个点到角两边的距离相等
这个点在这个角的平分线上
逆命题 如果一个点到角两边的距离相等，那么这个点在这个角的平分线上.
已知：如图，PD⊥OA，PE⊥OB，垂足分别是 D、E，PD = PE. 求证：点 P 在∠AOB 的角平分线上.
分析：为了证明点 P 在∠AOB 的平分线上，可以先作射线 OP，然后证明Rt△PDO≌Rt△PEO，从而得到∠AOP =∠BOP.
证明：作射线 OP，∵PD⊥OA，PE⊥OB，∴ ∠PDO = ∠PEO = 90°.在 Rt△PDO 和 Rt△PEO 中，OP = OP（公共边），PD = PE（已知），∴ Rt△PDO≌Rt△PEO ( H. L. ).
∴ ∠AOP =∠BOP（全等三角形的对应角相等）.∴ 点 P 在∠AOB 的平分线上.
应用格式：∵ PD⊥OA，PE⊥OB，PD = PE，∴点 P 在∠AOB 的平分线上.角平分线的判定定理与性质定理互为逆定理.
利用尺规作三角形的三条角平分线，你发现了什么？
发现：三角形的三条角平分线交于一点．
点拨：要证明三角形的三条角平分线交于一点，只需证明证明其中的两条角平分线的交点一定在第三条角平分线上即可.思路可表示如下：
试试看，你会写出证明过程吗？
例 如图，△ABC 的角平分线 BM，CN 相交于点 P. 求证：点 P 也在∠A 的平分线上.
证明：过点 P 作 PD⊥AB，PE⊥BC， PF⊥AC，垂足分别为 D、E、F.∵ BM 是△ABC 的角平分线，点 P 在 BM 上，∴ PD = PE.同理 PE = PF.
∴ PD = PF.∴ 点 P 在∠A 的平分线上，即点 P 到 AB、BC、CA 三边的距离相等.
1. 在你学过的定理中，有哪些定理的逆命题是真命题？试举出几个例子说明.同旁内角互补，两直线平行.(2) 有两个角相等的三角形是等腰三角形.
逆命题：两直线平行，同旁内角互补.
逆命题：如果一个三角形是等腰三角形，那么它有两个角相等.
2. 说出下列命题的逆命题，并判定逆命题的真假：① 既是中心对称，又是轴对称的图形是圆.② 有一组对边平行且相等的四边形是平行四边形.
③ 磁悬浮列车是一种高速行驶时不接触地面的交通工具.
1.如图所示，AC = AD，BC = BD，则下列说法正确的是（　　　）A．AB 垂直平分 CDB ．CD 垂直平分 AB C．AB 与 CD 互相垂直平分D．CD 平分∠ACB
2.已知线段 AB，在平面上找到三个点 D、E、F，使 DA＝DB，EA＝EB，FA＝FB，这样的点在组合共有_________种.
3.下列说法：①若点 P、E 是线段 AB 的垂直平分线上两点，则EA＝EB，PA＝PB；②若 PA＝PB，EA＝EB，则直线 PE 垂直平分线段AB；
③若 PA＝PB，则点 P 必是线段 AB 的垂直平分线上的点；④若 EA＝EB，则经过点 E 的直线垂直平分线段 AB．其中正确的有__________（填序号）.
4.在锐角三角形 ABC 内一点 P，满足 PA = PB = PC，则点 P 是△ABC ( )A.三条角平分线的交点B.三条中线的交点C.三条高的交点D.三边垂直平分线的交点
5.如图，△ABC 中，AB = AC，AB 的垂直平分线交交 AC 于 E，连接 BE，AB + BC = 16 cm，则△BCE 的周长是__________cm.
1. 如图，DE⊥AB，DF⊥BG，垂足分别是 E，F，DE = DF，∠FDB = 60°，则∠EBF = ______°，BE = ____________.
2. 如图，△ABC 中，∠C = 90°，DE⊥AB，∠CBE =∠ABE，且 AC = 6 cm，那么线段 BE 是∠ABC 的______________，AE + DE =______cm.
3. 已知：如图，△ABC 中，∠C = 90°，AD 是△ABC 的角平分线，DE⊥AB 于 E，F 在 AC 上，BD = DF. 求证：CF = EB.
证明：∵ AD 平分∠CAB，DE⊥AB，∠C＝90°，∴ CD＝DE.∵ 在 Rt△CDF 和 Rt△EDB 中， CD = ED，DF = DB，∴ Rt△CDF≌Rt△EDB ( H. L. ).∴ CF = EB.
一个定理的逆命题也是定理，这两个定理叫做互逆定理
第一个命题的条件是第二个命题的结论；第一个命题的结论是第二个命题的条件
线段的垂直平分的性质和判定
到线段两端点距离相等的点在线段的垂直平分线上
线段垂直平分线上的点到线段的两个端点的距离相等
见垂直平分线，得线段相等
判断一个点是否在线段的垂直平分线上
性质定理：角平分线上的点到角两边的距离相等
判定定理：角的内部到角两边距离相等的点在角的平分线上