

2022-2023学年四川省眉山市仁寿一中北校区高二(下)期中数学试卷(文科)(含解析)
展开2022-2023学年四川省眉山市仁寿一中北校区高二(下)期中数学试卷(文科)
一、单选题(本大题共12小题,共60.0分。在每小题列出的选项中,选出符合题目的一项)
1. 复数z满足z=2−ii+3i(i是虚数单位),则z的共轭复数z−对应的点在复平面内位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知函数f(x)=xsinx+cosx,则f′(x)=( )
A. xcosx B. −xcosx C. 2sinx+xcosx D. xsinx
3. 如图,这是甲、乙两位同学在4次数学测试中得分的茎叶图,若从甲、乙两位同学的4次得分中各抽选1次得分,则甲同学抽选的得分高于乙同学抽选的得分的概率为( )
A. 38 B. 716 C. 58 D. 916
4. 已知函数f(x)可导,且满足Δx→0limf(3−Δx)−f(3)Δx=2,则函数y=f(x)在x=3处的导数为( )
A. 2 B. 1 C. −1 D. −2
5. 已知复数1+i是关于x的方程x2+px+q=0(p,q∈R)的一个根,则|p+qi|=( )
A. 4 B. 2 3 C. 8 D. 2 2
6. 如图所示的程序框图,能使输入的x值与输出的y值相等的x值个数为( )
A. 1 B. 2 C. 3 D. 4
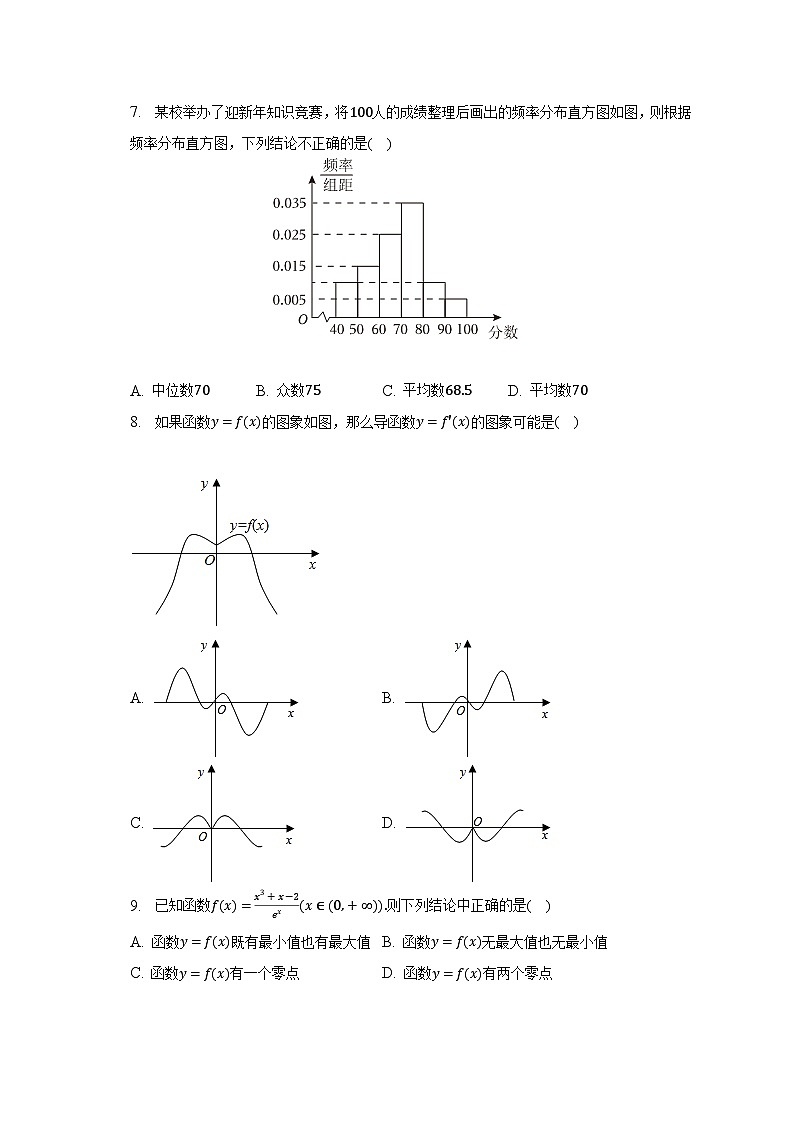
7. 某校举办了迎新年知识竞赛,将100人的成绩整理后画出的频率分布直方图如图,则根据频率分布直方图,下列结论不正确的是( )
A. 中位数70 B. 众数75 C. 平均数68.5 D. 平均数70
8. 如果函数y=f(x)的图象如图,那么导函数y=f′(x)的图象可能是( )
A. B.
C. D.
9. 已知函数f(x)=x3+x−2ex(x∈(0,+∞)).则下列结论中正确的是( )
A. 函数y=f(x)既有最小值也有最大值 B. 函数y=f(x)无最大值也无最小值
C. 函数y=f(x)有一个零点 D. 函数y=f(x)有两个零点
10. 已知函数f(x)=−x3+x−1,以下判断正确的是( )
①f(x)有两个极值点;
②f(x)有三个零点;
③点(0,−1)是f(x)曲线的对称中心.
A. ①② B. ②③ C. ①③ D. ①②③
11. 已知函数f(x)=ex−e−x+sinx,若f(t)+f(1−3t)<0,则实数t的取值范围是( )
A. (12,+∞) B. (−∞,12) C. (14,+∞) D. (−∞,14)
12. 设a=34e25,b=35,c=25e34,则( )
A. b
13. 在极坐标系中,点A(4,π6),B(2,π2),则线段AB的长为______ .
14. 某学校为了调查学生生活方面的日支出情况,抽出了一个容量为n的样本,将数据按[20,30),[30,40),[40,50),[50,60),[60,70]分成5组,制定成如图所示的频率分布直方图,则a= .要从日支出在[50,70]的样本中用分层抽样的方法抽取10人,则日支出在[60,70]中被抽取的人数为 .
15. 一个箱子的容积与底面边长x的关系为V(x)=x2(90−x2)(0
三、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题10.0分)
网络购物已经渐渐成为人们购物的新方式.为了调查每周网络购物的次数和性别的关系,随机调查了100名市民的网络购物情况,有关数据的2×2列联表如下:
10次及10次以上
10次以下
总计
男性
32
20
52
女性
43
5
48
总计
75
25
100
(1)从这100位市民中随机抽取一位,试求该市民为每周网络购物不满10次的男性的概率;
(2)请说明能否在犯错误的概率不超过0.05的前提下,认为每周网络购物次数与性别有关系?(已知P(χ2≥3.841)≈0.05)
[参考公式:χ2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)(其中n=a+b+c+d)]
18. (本小题12.0分)
设f(x)=x3−3x2−9x+a.
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若函数f(x)的极大值为10,求函数f(x)在[−2,2]上的最小值.
19. (本小题12.0分)
已知袋子中放有大小和形状相同标号分别是0,1,2的小球若干,其中标号为0的小球1个,标号为1的小球2个,标号为2的小球n个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是14.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的球标号为b.
①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,4]内任取2个实数x,y,求事件“x2+y2>(a−b)2恒成立”的概率.
20. (本小题12.0分)
已知函数f(x)=x−alnx.
(1)若f(x)在[1,+∞)上单调递增,求a的取值范围.
(2)求f(x)的单调区间.
21. (本小题12.0分)
如图是某采矿厂的污水排放量y(单位:吨)与矿产品年产量x(单位:吨)的折线图:
(1)依据折线图计算x,y的相关系数r,并据此判断是否可用线性回归模型拟合y与x的关系?(若|r|>0.75,则线性相关程度很高,可用线性回归模型拟合)
(2)若可用线性回归模型拟合y与x的关系,请建立y关于x的线性回归方程,并预测年产量为20吨时的污水排放量.
相关系数:r=i=1n(xi−x−)(yi−y−) i=1n(xi−x−)2i=1n(yi−y−)2,参考数据:i=15(xi−x−)(yi−y−)=19.
回归方程y =b x+a 中,b =i=1n(xi−x−)(yi−y−)i=1n(xi−x−)2,a =y−−b x−.
22. (本小题12.0分)
已知函数f(x)=lnx−2x+1,g(x)=mex+f(x)(m∈R,e为自然对数的底数).
(1)求函数f(x)的极值;
(2)若对∀x∈(0,+∞),g(x)<0恒成立,求m的取值范围.
答案和解析
1.【答案】C
【解析】解:因为z=−2i−11+3i=−1+i,
所以z−=−1−i,
所以z−在复平面上的对应点的坐标为(−1,−1),点(−1,−1)位于第三象限.
故选:C.
根据复数的运算求复数z的代数形式,根据共轭复数的定义求z−,根据复数的几何意义确定z−在复平面上的对应点的坐标,由此确定其象限.
本题主要考查复数的四则运算,共轭复数的定义,属于基础题.
2.【答案】A
【解析】解:f′(x)=x′sinx+x(sinx)′+(cosx)′=sinx+xcosx−sinx=xcosx.
故选:A.
根据导数运算法则直接求解即可.
本题主要考查导数的运算,属于基础题.
3.【答案】B
【解析】解:从甲、乙两位同学的4次得分中各抽选1次得分,
则共有16种情况,其中甲的得分高于乙的得分的情况有7种,
故所求的概率为716.
故选:B.
根据古典概型的概率公式即可求解.
本题主要考查了古典概型的概率公式,属于基础题.
4.【答案】D
【解析】解:函数y=f(x)在x=3处的导数为Δx→0limf(3)−f(3−Δx)Δx=−2,
故选:D.
利用导数的定义,即可得出结论.
本题考查导数的运用和导数的意义,比较基础.
5.【答案】D
【解析】解:因为复数1+i是关于x的方程x2+px+q=0(p,q∈R)的一个根,
所以复数1−i也是关于x的方程x2+px+q=0(p,q∈R)的一个根,
所以有1+i+1−i=2=−p,(1+i)(1−i)=2=q,解得p=−2,q=2,
所以|p+qi|=2 2.
故选:D.
据实系数一元二次方程根与系数关系进行求解即可.
本题主要考查复数的四则运算,属于基础题.
6.【答案】C
【解析】解:由程序框图知:程序的功能是求分段函数y=x2 x≤22x−3 2
若x≤2,由x2=x得x=0或1;
若2
综上x的值有0,1,3.
故选:C.
程序的功能是求分段函数y=x2 x≤22x−3 2
本题考查了选择结构的程序框图,根据框图流程判断算法的功能是关键.
7.【答案】D
【解析】解:[40,50)的频率为1−(0.015+0.025+0.035+0.005)×102=0.1,
因为最高小矩形的中点横坐标为75,显然众数是75,故B正确;
[40,50)的频率是0.1,[50,60)的频率是0.15,[60,70)的频率是0.25,其频率和为0.5,所以中位数为70,故A正确;
平均数=45×0.1+55×0.15+65×0.25+75×0.35+85×0.1+95×0.05=68.5,所以C正确.
故选:D.
根据题意,由频率分布直方图分别计算,即可得到结果.
本题主要考查了频率分布直方图的应用,考查了平均数、众数和中位数的估计,属于基础题.
8.【答案】A
【解析】解:由原函数的单调性可以得到导函数的正负情况依次是正→负→正→负,
故选:A.
由y=f(x)的图象得函数的单调性,从而得导函数的正负.
本题考查利用导数研究函数的单调性,属于基础题.
9.【答案】C
【解析】解:f′(x)=−x3+3x2−x+3ex=−(x−3)(x2+1)ex,x∈(0,+∞),x2+1>0,ex>0,
当x∈(0,3)时,f′(x)>0,函数单调递增;
当x∈(3,+∞)时,f′(x)<0,函数单调递减.
故函数有最大值,无最小值,AB错误,
设g(x)=x3+x−2,则g′(x)=3x2+1>0恒成立,函数单调递增,
且g(1)=1+1−2=0,故函数有一个零点,C正确,D错误.
故选:C.
求导得到导函数,确定函数的单调区间,得到函数有最大值,无最小值,AB错误,设g(x)=x3+x−2,函数单调递增,g(1)=0,故函数有一个零点,C正确,D错误,得到答案.
本题考查利用导数研究函数的单调性,最值以及函数零点,考查运算求解能力,属于基础题.
10.【答案】C
【解析】解:由f(x)=−x3+x−1得f′(x)=−3x2+1,
令f′(x)=0得x=± 33,且当x<− 33和x> 33时,f′(x)<0,当− 33
所以x=± 33均是f(x)的极值点,故f(x)有两个极值点,故①正确,
由①知,x= 33是f(x)的极大值点,且f( 33)=− 39+ 33−1<0,f(−2)=8−2−1>0,所以f(x)只有一个零点,故②错误,
又f(−x)=−(−x)3+(−x)−1=x3−x−1,所以f(x)+f(−x)=−2,故点(0,−1)是f(x)曲线的对称中心,所以③正确.
故选:C.
求导,根据导函数的正负可判断极值点,即可判断①,根据单调性以及极值即可判断②,根据对称性满足的关系式即可判断③.
本题主要考查利用导数研究函数的极值,函数零点个数的判断,函数的对称性,考查逻辑推理能力,属于中档题.
11.【答案】A
【解析】解:根据题意,f(x)=ex−e−x+sinx,其定义域为R,
有f(−x)=e−x−ex+sin(−x)=−(ex−e−x+sinx)=−f(x),则f(x)为奇函数,
又由f′(x)=ex+e−x+cosx>0,则f(x)在R上为增函数,
又由f(t)+f(1−3t)<0⇒f(t)<−f(1−3t)⇒f(t)
故选:A.
根据题意,先分析函数的奇偶性,求出函数的导数,分析可得f(x)在R上为增函数,由此可得f(t)+f(1−3t)<0⇒f(t)
12.【答案】A
【解析】解:ac=34e2525e34=e2525e3434,
令f(x)=exx,0
所以f(x)在(0,1)上单调递减,
所以f(25)>f(34),
所以ac>1,
所以a>c,
因为c=25e34,b=35,
所以c−b=25e34−35=25(e34−32)=25(e34−2×34),
令g(x)=ex−2x,
g′(x)=ex−2,
当x>ln2时,g′(x)>0,g(x)单调递增,
所以g(34)>g(ln2)=eln2−2ln2=2−2ln2>0,
所以c>b,
所以a>c>b,
故选:A.
根据题意可得ac=e2525e3434,令f(x)=exx,0
13.【答案】2 3
【解析】解:由已知A(4,π6),B(2,π2),
∴线段AB的长为|AB|= 42+22−2×4×2×cos(π2−π6)=2 3.
故答案为:2 3.
根据极坐标系中两点间的距离公式,求出线段AB的长即可.
本题主要考查极坐标刻画点的位置,属于基础题.
14.【答案】0.005 2
【解析】解:(2×a+0.02+0.025+0.045)×10=1,解得a=0.005,
因为[50,60)内和[60,70]内的样本个数比例为0.020:0.005=4:1,
根据分层抽样可知,日支出在[60,70]中被抽取的人数为10×11+4=2.
故答案为:0.005,2;
根据频率之和为1列出方程,求出a=0.005,得到[50,60)内和[60,70]内的样本比例,从而得到在[60,70]中被抽取的人数.
本题主要考查了频率分布直方图的应用,属于基础题.
15.【答案】60
【解析】解:V(x)=x2(90−x2)=45x2−12x3(0
令V′(x)=0得,x=60,
∴当x∈(0,60)时,V′(x)>0,V(x)单调递增;当x∈(60,90)时,V′(x)<0,V(x)单调递减,
∴当x=60时,V(x)取得最大值,
故答案为:60.
求出V′(x),根据V′(x)的正负,得到V(x)的单调性,进而求出V(x)最大时x的值.
本题主要考查了利用导数研究函数的最值,属于基础题.
16.【答案】e
【解析】解:f(x)的导数为2x,g(x)的导数为2ax,a≠0,
设公共切线与f(x)=x2+1的图象切于点(m,m2+1),
与g(x)=2alnx+1切于点(n,2alnn+1),
∴2m=2an=2alnn+1−m2−1n−m=2alnn−m2n−m,
化简可得,a=mn,2mn−2m2=2alnn−m2,
可得2a(1−lnn)=a2n2,
即有a2=n2(1−lnn),
设h(x)=x2(1−lnx),x>0,
则h′(x)=x−2xlnx,
∴h(x)在(0, e)上递增,在( e,+∞)上递减,
∴h(x)max=h( e)=e2,
∴实数a的取值范围为(−∞,e],
即a的最大值为e.
故答案为:e.
设公切线与f(x)、g(x)的切点坐标,由导数几何意义、斜率公式列出方程化简,分离出a后构造函数,利用导数求出函数的单调区间、最值,即可求出实数a的取值范围和最大值.
本题考查了导数的几何意义、斜率公式,导数与函数的单调性、最值问题的应用,及方程思想和构造函数法,属于中档题.
17.【答案】解:(1)由2×2列联表可得,每周网络购物不满10次的男性的概率为20100=0.2:
(2)由题意可得,χ2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)=100×(32×5−20×43)275×25×52×48≈10.47>3.841,
故在犯错误的概率不超过0.05的前提下,认为每周网络购物次数与性别有关系.
【解析】(1)由2×2列联表和古典概率公式可得所求值;
(2)由公式χ2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d),代入数据,计算可得结论.
本题考查古典概率的求法,以及独立性检验,考查运算能力,属于基础题.
18.【答案】(Ⅰ)f′(x)=3x2−6x−9=3(x−3)(x+1),
由f′(x)>0得x>3或x<−1,
∴f(x)的单调递增区间为(−∞,−1)和(3,+∞);
(Ⅱ)由(Ⅰ)知函数f(x)在x=−1处取得极大值,
即f(−1)=10,得a=5,
则f(x)=x3−3x2−9x+5,
∴f(x)在[−2,−1]上单调递增,在[−1,2]上单调递减,
又f(−2)=3,f(2)=−17,
∴f(x)在[−2,2]上的最小值为−17.
【解析】(Ⅰ)对f(x)求导,由f′(x)>0即可求解单调递增区间;
(Ⅱ)由极值的性质可求得a的值,再判定函数的单调性进而可得最小值.
本题主要考查利用导数研究函数的单调性、极值与最值,考查运算求解能力,属于基础题.
19.【答案】解:(1)根据从袋子随机抽取1个小球,取到标号为2的小球的概率是14,可得n1+2+n=14,
解得n=1.
(2)①从袋子中不放回地随机抽取2个球,共有基本事件12个,其中满足“a+b=2”的基事件有4个,
则P(A)=412=13.
②记“x2+y2>(a−b)2恒成立”为事件B,
则事件B等价于“x2+y2>4恒成立”,(x,y)可以看成平面中的点,则全部结果所构成的区域为Ω={(x,y)|0≤x≤4,0≤y≤4,x,y∈R},
而事件B构成的区域B={(x,y)|x2+y2>4,(x,y)∈Ω},如图所示:
所以P(B)=1−14π×2242=1−π16.
【解析】(1)利用从袋子随机抽取1个小球,取到标号为2的小球的概率是14,确定n的值.
(2)①从袋子中不放回地随机抽取2个球,共有基本事件12个,其中满足“a+b=2”的基事件有4个,再利用古典概型的概率公式可求解.
②记“x2+y2>(a−b)2恒成立”为事件B,则事件B等价于“x2+y2>4恒成立”,(x,y)可以看成平面中的点,确定全部结果所构成的区域,事件B所构成的区域,利用几何概型的概率公式求解即可.
本题主要考查了古典概型的概率公式和几何概型的概率公式,属于中档题.
20.【答案】解:(1)由题意得f(x)的定义域为(0,+∞),f′(x)=1−ax=x−ax,
当a≤0时,f′(x)>0,f(x)在(0,+∞)单调递增,满足题意;
当a>0时,由f′(x)=x−ax≥0得x<0(不符合题意,舍去)或x≥a,
要使f(x)在[1,+∞)上单调递增,则a≤1,即0
(2)由(1)得当a≤0时,f(x)在(0,+∞)单调递增,
当a>0时,f(x)在(a,+∞)单调递增,
由f′(x)=x−ax<0得0
当a>0时,f(x)的单调递增区间为(a,+∞),单调递减区间为(0,a).
【解析】(1)由题意得f(x)的定义域为(0,+∞),f′(x)=1−ax=x−ax,分类讨论a≤0和a>0,即可得出答案;
(2)根据(1)中结论可得单调区间.
本题考查利用导数研究函数的单调性,考查转化思想,考查逻辑推理能力和运算能力,属于中档题.
21.【答案】解:(1)由图中数据可得,x−=15×(1+2+3+4+5)=3,y−=15×(3+7+9+10+11)=8,
i=15(xi−x−)2=4+1+0+1+4=10,i=15(yi−y−)2=40,
i=15(xi−x−)(yi−y−)=19,
故r=i=1n(xi−x−)(yi−y−) i=1n(xi−x−)2i=1n(yi−y−)2=19 10×40=0.95>0.75,
故可用线性回归模型拟合y与x的关系.
(2)b =i=1n(xi−x−)(yi−y−)i=1n(xi−x−)2=1910=1.9,a =8−1.9×3=2.3,
故y关于x的线性回归方程为y=1.9x+2.3,
当x=20时,y=1.9×20+2.3=40.3.
【解析】(1)根据已知条件,结合相关系数的公式,即可求解;
(2)根据已知条件,结合最小二乘法公式,求出线性回归方程,再将x=20代入上式方程,即可求解.
本题主要考查线性回归方程的求解,考查转化能力,属于中档题.
22.【答案】解:(1)∵f(x)定义域为(0,+∞),f′(x)=3−lnxx2,
∴当x∈(0,e3)时,f′(x)>0;当x∈(e3,+∞)时,f′(x)<0;
∴f(x)在(0,e3)上单调递增,在(e3,+∞)上单调递减,
∴f(x)的极大值为f(e3)=1e3+1,无极小值.
(2)由g(x)<0得:mex+lnx−2x+1<0,∴m<2−lnx−xxex在(0,+∞)上恒成立;
令h(x)=2−lnx−xxex,则h′(x)=(−1x−1)x−(2−lnx−x)(x+1)x2ex=(x+1)(x−3+lnx)x2ex;
令φ(x)=x−3+lnx,则φ′(x)=1+1x=x+1x>0,∴φ(x)在(0,+∞)上单调递增,
又φ(2)=ln2−1<0,φ(3)=ln3>0,∴∃x0∈(2,3),使得φ(x0)=0,则lnx0=3−x0,
∴当x∈(0,x0)时,h′(x)<0;当x∈(x0,+∞)时,h′(x)>0;
∴h(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,∴h(x)min=h(x0)=2−lnx0−x0x0ex0;
由lnx0=3−x0得:lnx0+lnex0=ln(x0ex0)=3,∴x0ex0=e3,
∴h(x)min=h(x0)=2−lnx0−x0x0ex0=−1e3,∴m<−1e3,
则实数m的取值范围为(−∞,−1e3).
【解析】(1)求导后,根据f′(x)的正负可求得f(x)的单调性,根据极值的定义可求得结果;
(2)分离变量可将问题转化为m
2023-2024学年四川省眉山市仁寿第一中学校(北校区)高二上学期期中数学试题含答案: 这是一份2023-2024学年四川省眉山市仁寿第一中学校(北校区)高二上学期期中数学试题含答案,文件包含四川省眉山市仁寿第一中学校北校区2023-2024学年高二上学期期中数学试题Word版含解析docx、四川省眉山市仁寿第一中学校北校区2023-2024学年高二上学期期中数学试题Word版无答案docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
四川省眉山市仁寿第一中学校(北校区)2023-2024学年高二上学期期中数学试题(Word版附解析): 这是一份四川省眉山市仁寿第一中学校(北校区)2023-2024学年高二上学期期中数学试题(Word版附解析),共18页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年四川省眉山市仁寿县文宫中学高一(下)期中数学试卷(含解析): 这是一份2022-2023学年四川省眉山市仁寿县文宫中学高一(下)期中数学试卷(含解析),共16页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












