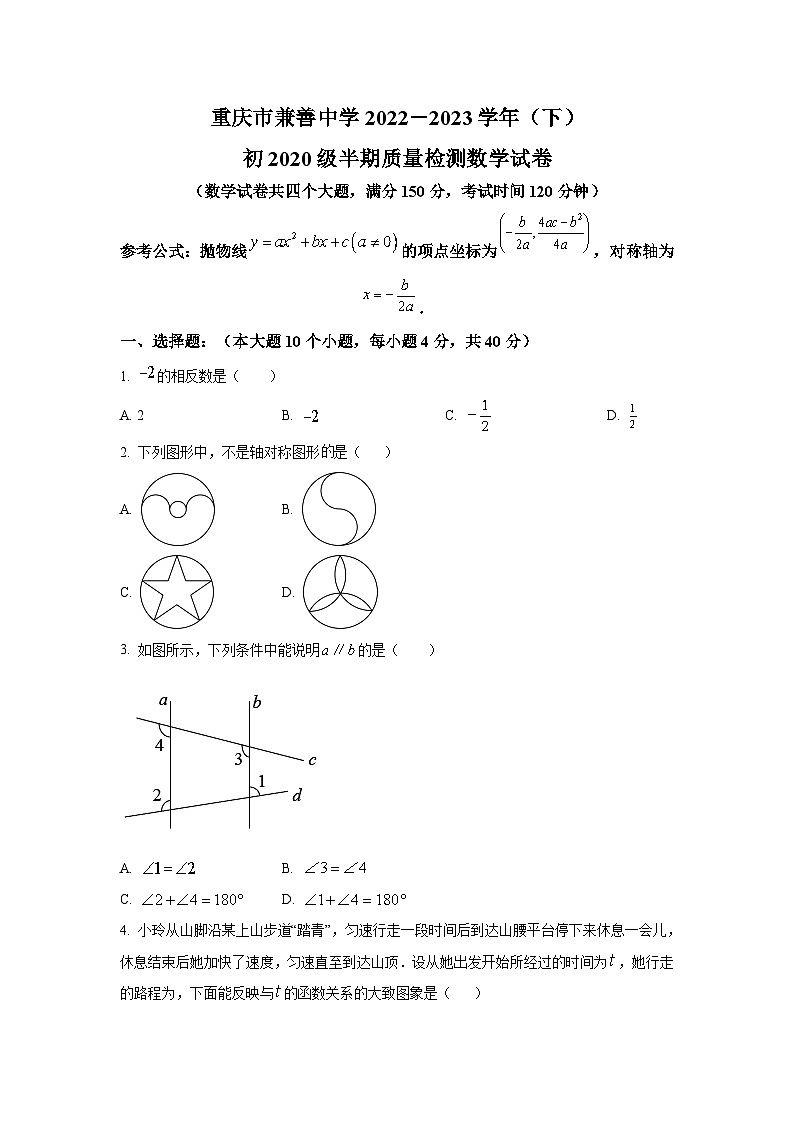
重庆市兼善中学2023届九年级下学期半期质量检测数学试卷(含解析)

这是一份重庆市兼善中学2023届九年级下学期半期质量检测数学试卷(含解析)，共28页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
重庆市兼善中学2022－2023学年（下）
初2020级半期质量检测数学试卷
（数学试卷共四个大题，满分150分，考试时间120分钟）
参考公式：抛物线的项点坐标为，对称轴为．
一、选择题：（本大题10个小题，每小题4分，共40分）
1. 的相反数是（ ）
A. 2 B. C. D.
2. 下列图形中，不是轴对称图形是（ ）
A. B.
C. D.
3. 如图所示，下列条件中能说明的是（　　）

A. B.
C. D.
4. 小玲从山脚沿某上山步道“踏青”，匀速行走一段时间后到达山腰平台停下来休息一会儿，休息结束后她加快了速度，匀速直至到达山顶．设从她出发开始所经过的时间为，她行走的路程为，下面能反映与的函数关系的大致图象是（ ）
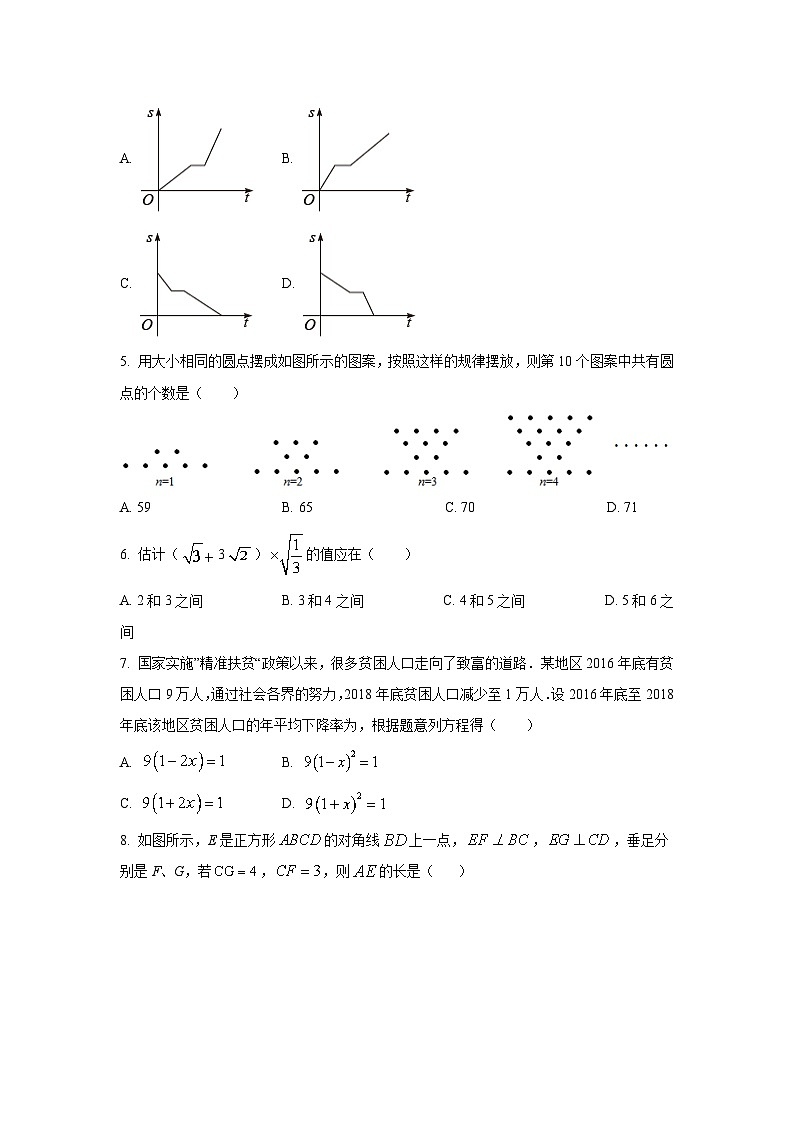
A. B.
C. D.
5. 用大小相同的圆点摆成如图所示的图案，按照这样的规律摆放，则第10个图案中共有圆点的个数是（　　）

A. 59 B. 65 C. 70 D. 71
6. 估计（3）的值应在（　　）
A. 2和3之间 B. 3和4之间 C. 4和5之间 D. 5和6之间
7. 国家实施”精准扶贫“政策以来，很多贫困人口走向了致富的道路．某地区2016年底有贫困人口9万人，通过社会各界的努力，2018年底贫困人口减少至1万人．设2016年底至2018年底该地区贫困人口的年平均下降率为，根据题意列方程得（　　）
A. B.
C. D.
8. 如图所示，E是正方形的对角线上一点，，，垂足分别是F、G，若，，则的长是（ ）

A. 3 B. 4 C. 5 D. 7
9. 如图，在中，是边上的点，以为圆心，为半径的与相切于点，平分，，，的长是（　　）

A. B. 2 C. D.
10. 有n个依次排列的整式：第一项是a2，第二项是a2+2a+1，用第二项减去第一项，所得之差记为b1，将b1加2记为b2，将第二项与b2相加作为第三项，将b2加2记为b3，将第三项与b3相加作为第四项，以此类推；某数学兴趣小组对此展开研究，得到4个结论：
①b3＝2a+5；
②当a＝2时，第3项为16；
③若第4项与第5项之和为25，则a＝7；
④第2022项为（a+2022）2；
⑤当n＝k时，b1+b2+…+bk＝2ak+k2；
以上结论正确的是（　　）
A. ①②⑤ B. ①③⑤ C. ①②④ D. ②④⑤
二、填空题：（本大题8个小题，每小题4分，共32分）
11. ______．
12. 数据600000用科学记数法表示为______．
13. 在一个不透明的袋中装有除颜色外其余都相同的4个小球，其中2个红球、2个黄球，如果第一次先从袋中摸出1个球后不放回，第二次再从袋中摸出1个球，那么两次都摸到黄球的概率是______．
14. 如图，与位似，位似中心是点，若，则与的周长比是______．

15. 如图在正方形中，点是以为直径半圆与对角线的交点，若圆的半径等于，则图中阴影部分的面积为_____．

16. 如图，三角形纸片ABC中，点D，E，F分别在边AB，AC，BC上，BF＝4，CF＝6，将这张纸片沿直线DE翻折，点A与点F重合．若DE∥BC，AF＝EF，则四边形ADFE的面积为__________．

17. 若关于x的不等式组有解，关于y的分式方程有非负数解，则符合条件的所有整数a的和为______．
18. 两位数m和两位数n，它们各个数位上的数字都不为0，将数m任意一个数位上的数字作为一个新的两位数的十位数字，将数n任意一个数位上的数字作为该新的两位数的个位数字，按照这种方式产生的所有新的两位数的和记为，例如：；，若一个两位数，两位数（，，x，y是整数），交换两位数的十位数字和个位数字得到新数，当与的个位数字的6倍的和能被整除时，称这样的两个数和为“美好数对”，求所有“美好数对”中的最小值______．
三、解答题：（本大题共2个小题，19小题10分，20小题8分，共18分）解答时每小题必须给出必要的演算过程成推理步骤，画出必要的图形（包括作辅助线），请将解答过程书写在答题卡中对应的位置上．
19. 计算：
（1）（x+y）2+y（3x-y）
（2）
20. 如图，在平行四边形中，平分交于E．

（1）用尺规作图完成以下基本作图：作线段的垂直平分线，分别交，于点M，N．连接；（保留作图痕迹，不写作法和结论．）
（2）根据（1）中作图，证明四边形是菱形，请你补全证明过程．
证明：∵四边形是平行四边形，
∴
∴
又∵平分
∴ ①
∴
∴ ②
∴点A在直线上
又∵
∴ ③
∴
又∵，
∴四边形是平行四边形
又∵
∴ ④
四、解答题：（本大题共6个小题，每小题10分，共60分）
21. 2022年4月16日9时56分，神舟十三号载人飞船返回舱在东风着陆场成功着落，神舟十三号载人飞行任务取得圆满成功，中国航天又达到了一个新的高度．某校为了了解本校学生对航天科技的关注程度，对八、九年级学生进行了航天科普知识竞赛（百分制），并从其中分别随机抽取了20名学生的测试成绩，整理、描述和分析如下：（成绩得分用x表示，共分成四组：A．；B．；C．；D．）其中，八年级20名学生的成绩是：96，80，96，91，99，96，90，100，89，82，85，96，87，96，84，81，90，82，86，94．
九年级20名学生的成绩在C组中的数据是：90，91，92，92，93，94．
八、九年级抽取的学生竞赛成绩统计表
年级
平均数
中位数
众数
方差
八年级
90
90
b
38.7
九年级
90
c
100
38.1

根据以上信息，解答下列问题：
（1）直接写出上述a、b、c的值：a＝　 　，b＝　 　，c＝　 　；
（2）你认为这次比赛中哪个年级的竞赛成绩更好，为什么？
（3）若该校九年级共1400人参加了此次航天科普知识竞赛活动，估计参加此次活动成绩优秀（）的九年级学生人数．
22. 在全民健身运动中，跑步运动颇受市民青睐，甲、乙两跑步爱好者约定从A地沿相同路线跑步去距A地8千米的B地，已知甲跑步的速度是乙的1.2倍．
（1）若乙先跑步1千米，甲才开始从A地出发，则甲出发半小时恰好追上乙，求甲跑步速度；
（2）若乙先跑步10分钟，甲才开始从A地出发，则甲、乙恰好同时到达B地，求甲跑步的速度．
23. 如图，笔直的海岸线l上有A、B两个观测站，A在B的正东方向．有一艘渔船在点P处，从A处测得渔船在北偏西的方向，从B处测得渔船在其东北方向，且测得B、P两点之间的距离为20海里．

（1）求观测站A、B之间的距离（结果保留根号）；
（2）渔船从点P处沿射线的方向航行一段时间后，到点C处等待补给，此时，从B测得渔船在北偏西的方向．在渔船到达C处的同时，一艘补给船从点B出发，以每小时20海里的速度前往C处，请问补给船能否在83分钟之内到达C处？（参考数据：）
24. 如图，在中，，厘米，厘米，点P从点B出发，沿以每秒1厘米速度匀速运动到点A，设点P的运动时间为x秒，B、P两点间的距离为y厘米．小新根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究，下面是小新的探究过程，请补充完整：

（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
x（）
0
1
2
3
4
5
6
7
y（）
0







m的值是______；当时，y与x的函数关系式是______．
（2）先补全平面直角坐标系，再画出该函数的图象，并写出函数图象的性质：______（写出一条即可）．

（3）结合画出的函数图象，解决问题：在曲线部分的最低点时，P运动的时间为______秒．
25. 如图，在平面直角坐标系中，抛物线与x轴交于两点（点A在点B左侧），与y轴交于点C，连接，点P为直线上方抛物线上一动点，连接交于点Q．

（1）求抛物线的函数表达式；
（2）当的值最大时，求点P的坐标和的最大值；
（3）把抛物线向右平移1个单位，再向上平移2个单位得新抛物线，M是新抛物线上一点，N是新抛物线对称轴上一点，当以M、N、B、C为顶点的四边形是平行四边形时，写出所有符合条件的N点的坐标，并写出求解点N的坐标的其中一种情况的过程．
26. 已知正方形的边长为4，为等边三角形，点E在边上，点F在边的左侧．

（1）如图1，若D，E，F在同一直线上，求的长；
（2）如图2，连接，并延长交于点H，若，求证：
（3）如图3，将沿翻折得到，点Q为的中点，连接，若点E在射线上运动时，请直接写出线段的最小值．

答案

1. A
解：的相反数是：，
故选：A．
2. B
解：A是轴对称图形，故不符合题意；
B不是轴对称图形，故符合题意；
C是轴对称图形，故不符合题意；
D是轴对称图形，故不符合题意；
故选：B．
3. B
A．当时，不能判定，故选项不符合题意；
B．当时，与属于同位角，能判定，故选项符合题意；
C．当时，与属于同旁内角，能判定，故选项不符合题意；
D．当时，不能判定，故选项不符合题意；
故选：B．
4. A
解：∵一开始时，小玲匀速行驶，
∴一开始的阶段，路程与时间的函数图象是一条直线，且s随t增大而增大
∵在第一段匀速行走后休息了一段时间，
∴在休息的时间段内，路程是不发生变化的，即此时函数图象是平行于时间轴的一条线段
∵在休息过后继续匀速行走且比第一次匀速行走的速度快，
∴最后一段函数图象也是一条直线，且比一开始的那段直线陡，且s随t增大而增大，
故只有A符合题意，
故选A．
5. C
解：根据图中圆点排列，
当n＝1时，圆点个数5+2；
当n＝2时，圆点个数5+2+3；
当n＝3时，圆点个数5+2+3+4；
当n＝4时，圆点个数5+2+3+4+5，…
∴当n＝10时，圆点个数5+2+3+4+5+6+7+8+9+10+11
＝4+（1+2+3+4+5+6+7+8+9+10+11）
＝
．
故选：C．
6. C
解：根据图中圆点排列，
当n＝1时，圆点个数5+2；
当n＝2时，圆点个数5+2+3；
当n＝3时，圆点个数5+2+3+4；
当n＝4时，圆点个数5+2+3+4+5，…
∴当n＝10时，圆点个数5+2+3+4+5+6+7+8+9+10+11
＝4+（1+2+3+4+5+6+7+8+9+10+11）
＝
．
故选：C．
7. B
解：设这两年全省贫困人口的年平均下降率为，根据题意得：
，
故选B．
8. C
解：如图，连接CE，

∵四边形是正方形，BD是对角线，
∴∠BCD=90°，∠ABE=∠CBE=45°，AB=BC，
在△ABE和△CBE中
，
∴△ABE≌△CBE，
∴AE=CE，
∵EF⊥BC，EG⊥CD，
∴∠EGC=∠CFE=90°，
∴∠EGC=∠CFE=∠BCD=90°，
∴四边形EFCG是矩形，
∴EF=CG=4，
根据勾股定理得，CE=，
．
故选：C．
9. A
解：∵ 与AC相切于点D，

故选A．
10. A
解：第一项是a2，
第二项是a2+2a+1，
用第二项减去第一项，所得之差记为b1，则，
将b1加2记为b2，则，
将第二项与b2相加作为第三项，则第三项是，
当a＝2时，第三项是，②正确；
将b2加2记为b3，则，①正确；
第三项与b3相加作为第四项，则第四项是，
将b3加2记为b4，则，
第四项与b4相加作为第五项，则第五项是，
第4项与第5项之和为25，则，解得a＝0或，③错误；
…
综上所述：，第项为，
第2022项为，④错误；
当时，
，
故选：A．
11. 4
解：．
故答案为：4
12.
解：的绝对值大于表示成的形式，
∵，，
∴用科学记数法表示为，
故答案：．
13.
解：画树状图如图：

共有12种等可能的结果，两次都摸到黄球的结果有2种，
∴两次都摸到黄球的概率，
故答案为：．
14.
解： 与位似，
，，
，
，
与的周长比为，
故答案为：．
15. 1.
如图所示：连接，

可得，，，
且阴影部分面积
故答案为
16.
解：∵将这张纸片沿直线DE翻折，点A与点F重合，
∴DE垂直平分AF，，，，
∵DE∥BC，
∴，，，
∴，
∴，
∴，即D为AB的中点，
∴DE为的中位线，
∴，
∵AF＝EF，
∴是等边三角形，
在中，，，
∴，
∴，
∴四边形ADFE的面积为，

故答案为：．
17. 1
解：解不等式，得，
解不等式，得，
∵不等式组有解，
∴，
∴，
得，
∵，
∴，
∵分式方程有非负数解，
∴，且
解得且，
∴且，
∴符合条件的整数a有，
∴符合条件的所有整数a的和为．
故答案为：1．
18.
解：∵


∵，，x，y是整数
∴，
∴的十位数字和个位数字分别是：，
∴的十位数字和个位数字分别是：，
∴
∵
∴
∵
∴的个位数字是
∴与的个位数字的6倍的和为：

由题意知，当是整数，即能被整除时，两个数和为“美好数对”．
∵，，是整数
∴
∴
当时，
此时，，
“美好数对”和，
此时；
当时，
此时，，
“美好数对”为和，
此时；
综上所述：所有“美好数对”中的最小值为．
19. 解：（1）原式=x2+2xy+y2+3xy-y2=x2+5xy．
（2）原式=
=
=．
20. （1）
解：作图如下：

（2）
证明：∵四边形是平行四边形，
∴，
∴，
又∵平分，
∴①，
∴，
∴②，
∴点A在直线上．
又∵，
∴③，
∴，
又∵，，
∴四边形是平行四边形，
又∵，
∴四边形是菱形④．
故答案为：①；②；③；④四边形是菱形．
21. （1）
，
故；
八年级抽取的学生竞赛成绩出现最多的是96分，故众数；
九年级20名学生的成绩从小到大排列，排在中间的第10、11个数分别为92、93，故中位数；
故答案为：40，96，92.5；
（2）
九年级的成绩相对更好，理由如下：
九年级测试成绩的众数大于八年级；九年级测试成绩的方差小于八年级。
（3）
（人），
答：估计参加此次活动成绩优秀（）的九年级学生人数为980人．
22. （1）
设乙跑步的速度为千米时，则甲跑步的速度为千米时，
依题意得：，
解得：，
．
答：甲跑步的速度为12千米时．
（2）
设乙跑步的速度为千米时，则甲跑步的速度为千米时，
依题意得：，
解得：，
经检验，是原方程的解，且符合题意，
．
答：甲跑步的速度为9.6千米时．
23. （1）
解：过点P作于D点，

∴，
在中，，海里，
∴（海里）， （海里），
在中，，
∴（海里），
∴海里，
∴观测站A，B之间距离为海里；
（2）
补给船能在82分钟之内到达C处，
理由：过点B作，垂足为F，

∴，
由题意得：，，
∴，
在中，，
∴海里，
在中，，
∴海里，
∴补给船从B到C处的航行时间（分钟）分钟，
∴补给船能在83分钟之内到达C处．
24. （1）
解：根据表可知，运动，即，
∵，
∴，
∵，
∴是等边三角形，
∴，即，
根据题意得：当时，y是关于x的正比例函数，
设当时，y与x的函数关系式是，
把点代入得：，
∴当时，y与x的函数关系式是；
故答案为：3；
（2）
解：补全平面直角坐标系如下图，描点，连线，画图象如下，

性质：当时，y随x的增大而增大；
故答案为：当时，y随x的增大而增大
（3）
解：P点位置如图，

此时曲线位置为最低点，，
∵，
∴，
∴，
∴运动时间，
故答案为：．
25. （1）
解：抛物线与x轴交于、两点（点A在点B的左侧），
，
解得：，
抛物线的函数表达式为；
（2）
解：抛物线与y轴交于点C，
，
，
设直线的解析式为，把，代入，得：
，
解得：，
直线的解析式为，
如图1，过点P作轴交于点D，

设，则，
，
，
，
，
当时，取得最大值，此时，；
（3）
解：∵向右平移1个单位，再向上平移2个单位得新抛物线，
新抛物线解析式为，对称轴为直线，
设，，
①当为的边时，
则，，
，
解得：，

；
②当为的边时，
则，，
，
解得：，
；
③当为的对角线时，
则，
解得：，
；
综上所述，N点的坐标为： 或或．
26. （1）
解：∵为等边三角形，
∴，
∵四边形是正方形，
∴，，
∴，
∴，
∴；
（2）
证明：如图，延长，交于点G，

∵四边形是正方形，
∴，
∴，
∵，
∴，
∴，
∴，
∴，
∴，
∵为等边三角形，
∴，
∴，
∴，
∴，
∴，
∴，
∵，
∴，
∴，
∴，
∴，
∴；
（3）
解：当点E在线段上时，如图，取的中点N，连接，

∵将沿翻折得到，
∴，
∵点Q为的中点，
∴，
∴，
∴点Q在过线段的中点，且与成角的直线上移动，
∴当时，有最小值，
如图，延长，交于点H，连接，

∵点N是线段的中点，
∴，
∵，
∴，
∴，
∴，
∵，
∴，，，
∴，
∴，
∴此时点E不在线段上，
∴点E在线段上时，，
当点E在线段的延长线上时，

∵将沿翻折得到，
∴，
∵点Q为的中点，点N是线段的中点，
∴，
∴，
∴点Q在过线段的中点，且与成角的直线上移动，
∴当时，有最小值，
同理：；
综上所述，的最小值为．