数学八年级上册4.1 平方根完整版课件ppt

这是一份数学八年级上册4.1 平方根完整版课件ppt，共56页。PPT课件主要包含了1平方根，特别解读，易错警示，知识储备，1练习等内容，欢迎下载使用。

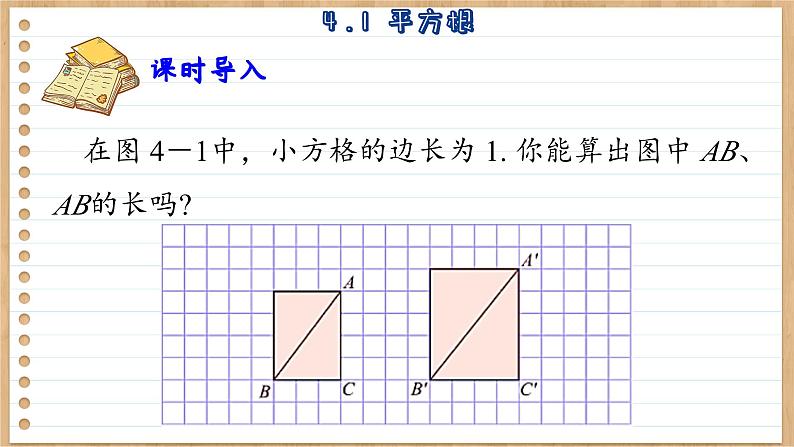
在图 4－1中，小方格的边长为 1. 你能算出图中 AB、AB的长吗?
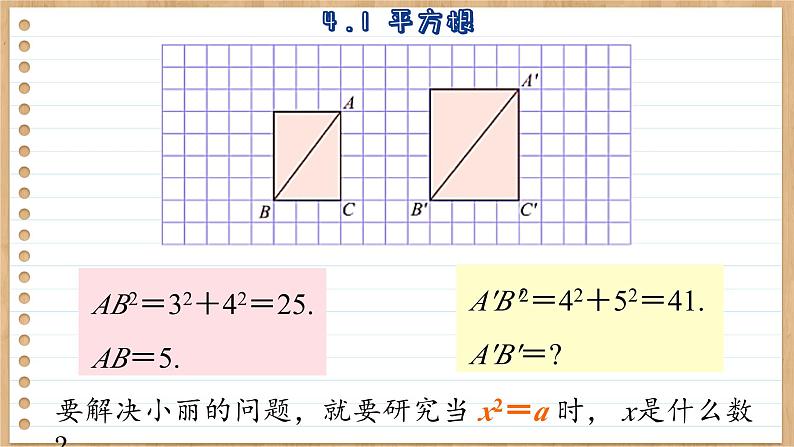
AB2＝32＋42＝25. AB＝5.
A′B′2＝42＋52＝41. A′B′＝?
要解决小丽的问题，就要研究当 x2＝a 时， x是什么数?
当 x2＝4 时，因为 22＝4，(－2)2＝4，所以 x＝±2； 当 x2＝100 时，因为 102＝100，(－10)2＝100，所以 x＝±10； 当 x2＝169 时，因为132＝169，(－13)2＝169，所以 x＝±13.
可以看出，使 x2＝a (a＞0) 成立的数有两个，它们互为相反数.
如果 x2＝a (a ＞0) 那么叫做 a 的平方根，也称为二次方根.
知识点 1 平方根
下列各数有平方根吗? 如果有，请写出来；如果没有，请说明理由.
一个正数有两个平方根，它们互为相反数； 0的平方根是0； 负数没有平方根.
求一个数的平方根的运算叫做开平方.
(1) 一个正数的平方根是2a－1 和a－5，则这个正数是多少？
解：根据题意，得(2a－1) ＋(a－5)＝0， 解得 a＝2， ∴这个正数为(2a－1)2＝ (2×2－1)2＝9.
(2) 已知2a－1 与－a+2 是 m 的平方根，求 m 的值.
解：根据题意，分以下两种情况： ① 当2a－1＝－a＋2 时，a＝1， ∴ m＝ (2a－1)2＝ (2×1－1)2＝1. ② 当(2a－1) ＋(－a＋2) ＝0 时，a＝－1， ∴ m＝ (2a－1)2＝[2×(－1)－1]2＝ (－3)2＝9. 故m 的值为1 或9.
知识点 2 算术平方根
1. 区分清楚算术平方根是平方根中的一个；2. 求一个正数的平方根时，不能遗漏负的平方根.
例2 求下列各数的算术平方根： (1) 625； (2) 0.008 1； (3) 7.
求一个数的算术平方根必须明确两点： 1. 这个数是非负数； 2 .求出的算术平方根(结果)必须是非负数.
小丽站在海边的一块岩石上，眼睛离海平面的高度h为 20 m，她观测到远处一艘船刚露出海平面，求此时d的值.
已知直角三角形的两边长分别为3 和4，求第三边的长.
1. 定义： 若x2＝a，则x叫做a的平方根.2. 性质： 一个正数有两个平方根，它们互为相反数， 0的平方根是0，负数没有平方根.
3. 平方根与开平方间的关系： (1)开平方是求平方根的运算； (2)平方根是开平方运算的结果.
4. 求一个非负数的平方根的方法： ① 求一个非负数a的平方根，就是要把平方后等于a的 数找出来，从而求出a的所有平方根； ② 求带分数的平方根时，应先将带分数化为假分数， 这也是常出错的地方.注意：正数的平方根有两个，前面必定有“±”号.
1. 写出下列各数的平方根：
2. 写出下列各数的算术平方根：
(3) x2＝15； (4) 4x2＝81.
4. 在△ABC中，∠C＝90°. (1) 已知 AC＝5，BC＝12，求AB；
(2) 已知 AC＝2，BC＝3，求AB；
(3) 已知 AB＝25，BC＝24，求AC.
5. (1) 已知直角三角形的两条直角边的长分别为3和5， 求斜边的长；
(2) 已知直角三角形的两边的长分别为3和5，求第三 边的长.
(2) 曾被誉为世界七大奇迹之一、建于公元前 3世纪毁于地震的亚历山大灯塔，用青铜反光镜反射阳光或灯火，反光镜高于海平面 125 m，它反射的光能照到离灯塔 35 km 的海面上.