苏科版数学八上6.6 一次函数、一元一次方程和一元一次不等式 （课件PPT）

这是一份苏科版数学八上6.6 一次函数、一元一次方程和一元一次不等式 （课件PPT），共37页。

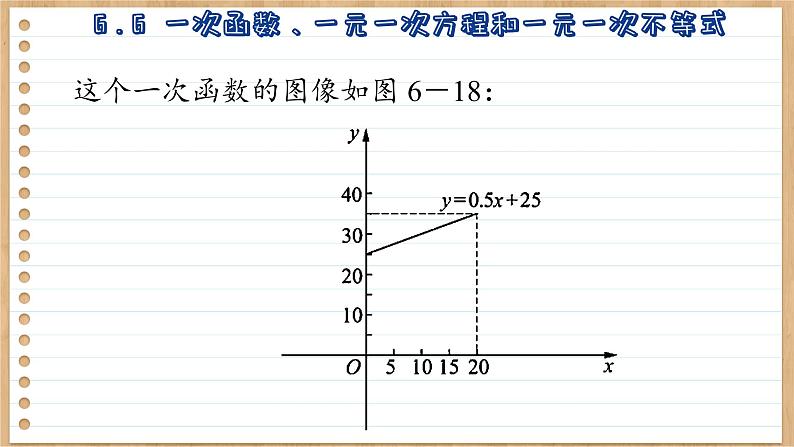
第6章 一次函数6 . 6一次函数、一元一次方程和一元一次不等式 一根长 25 cm 的弹簧，一端固定，另一端挂物体，在弹簧伸长后的长度不超过 35 cm 的限度内，每挂 1 g 质量的物体，弹簧伸长0.5cm. 设所挂物体的质量为x kg，弹管的长度为 y cm，写出y与x之间的函数表达式，画出函数图像，并求这根弹簧在所允许的限度内所挂物体的最大质量. 根据题意，挂 x kg 质量的物体后，这根弹簧伸长了 0.5x cm，弹簧的长度是(0.5x＋25)cm，y 与 x 之间的函数表达式为y＝0.5x＋25.这个一次函数的图像如图 6－18： 弹簧所挂物体的质量越大，弹簧的长度也越长. 因为挂上物体后该弹簧的长度不能超过 35 cm，所以当 y＝35 时，该弹所挂物体的质量最大.解一元一次方程0.5x＋25 ＝ 35，得x＝20.该弹簧所挂物体的最大质量是 20 kg. 能否用一元一次不等式求这根弹簧在所允许的限度内所挂物体的最大质量? 能用一元一次不等式求这根弹簧在所允许的限度内所挂物体的最大质量. 因为弹簧伸长后的长度不超过35 cm，所以y＜35，即0.5x＋25≤35，解得 x≤20. 所以该弹管在所允许的限度内所挂物体的最大质量是 20 kg.练 1 若一次函数 y＝kx＋b (k≠0)的图像经过(4，0)和(3，2)两点，则方程kx＋b＝4 的解为(　　) A. x＝0　　　　　B. x＝2　　　 C. x＝3　　　　　D. x＝5B练 2 如图，一次函数 y＝ax＋b 和 y＝kx＋c 的图像交于点P(2，4)， 则关于x 的一元一次方程 ax＋b＝kx＋c 的解是 _________.x ＝ 2 试根据一次函数y＝2x＋4的图像(如图6－19)说出2x＋4＝0、2x＋4＞0、2x＋4＜0的解. 根据一次函数 y＝2x＋4 的图像可知，此函数图像与x轴的交点坐标为(－2，0)， ∴一元一次方程 2x＋4＝0的解为x＝－2； 当函数图像在 x 轴上方，即 y＞0时，x＞－2， ∴一元一次不等式 2x＋4＞0 的解集是x＞－2； 同理，2x＋40 的解集是 x＜－2. 一次函数、一元一次方程、一元一次不等式有着紧密的联系. 已知一次函数的表达式，当其中一个变量的值确定时，可以由相应的一元一次方程确定另一个变量的值； 当其中一个变量的取值范围确定时，可以由相应的元一次不等式确定另一个变量的取值范围. 一辆汽车行驶 35 km 后，驶入高速公路，并以105 km/h 的速度速行驶了x h. 试根据上述情境，提出一些问题，并用一次函数、一元一次方程或一元一次不等式求解. (1)写出关于总路程 y(km)与时间 x (h)的一次函数表达式. 表达式为 y＝105x＋35.(2) 行驶了多少小时,行驶的总路程为245 km? 105x＋35＝245， 解得 x＝2. 故行驶了2h，行驶的总路程为 245 km.(3) 行驶了多少小时，行驶的总路程大于 350 km? 由105x＋35＞350， 解得x＞3. 故行驶的时间大于 3 h.(答案不唯一)练 3 如图，已知函数 y1＝ 3x＋b 和y2＝ax－3的图像交于点P(－2， －5)，则根据图像可得不等式 3x＋b＞ax－3 的解集是(　　) A. x ＞ －2　　　　　B. x ＜ －2 C. －2 ＜ x ＜ 0　　　D. x ＞ 0A1. x 取什么值时，函数 y＝－2(x＋1)＋4 的值是正数? 负数?非负数? 解：画出函数 y＝－2(x＋1)＋4 的图像如图所示，观察图像可知，当 x＜1时，函数 y＝－2(x＋1)＋4的值是正数；当 x＞1时，函数 y＝－2(x＋1)＋4 的值是负数；当 x＜1时，函数 y＝－2(x＋1)＋4 的值是非负数.  (2) 音速超过 340 m/s 时的气温范围. 一次函数、一元一次方程和一元一次不等式6 . 6 练习1. 画出函数 y＝2x＋4的图像，并根据图像写出下列方程 或不等式的解：(1) 2x＋4 ＝6；(2) 2x＋4＞6；(3) 2x＋4＜6.(1) 2x＋4＝6的解是x＝1(2) 2x＋4＞6的解集是x＞1(3) 2x＋4＜6 的解集是x＜1解：函数 y＝2x＋4的图像如图所示.2. x取什么值时，函数 y＝－3x＋1的值大于－2? 小于－2? 等于－2?解：函数 y＝－3x＋1 的图像如图所示. 由图像可知，当x＜1时，y＝ －3x＋1的值大于－2； 当x＞1时，y＝－3x＋1的值小于－2； 当x＝1时，y＝－3x＋1的值等于－2.3. 已知二元一次方程 x＋2y＝－5，当 x 取什么值时，y 的值是正数?负数?非负数? 由图像可知，当 x＜－5时，y 的值是正数；当x ＞－5时，y 的值是负数；当 x≤－5 时，y 的值是非负数.4. 某长途汽车客运公司规定旅客可免费携带一定质量的 行李，当行李的质量超过规定时，需付的行李费y(元) 与行李质量 x(kg)之间的函数表 达式为 y＝kx＋b，这个函数的 图像如图所示，求：(1) k和b的值；(2) 旅客最多可免费携带行李的质量；(3) 行李费为 4～15 元时，旅客携带行李的质量为多少?数学活动 摄氏温度用符号 T 表示，单位是℃(摄氏度)；华氏温度用符号F表示，单位是℉ (华氏度).温度计上的一次函数 (1) 取一只标有两种温标刻度的温度计(图6－20)，观察两种刻度间的关系，并将观察结果填入下表： (2) 在以 T 为横轴、F 为纵轴的平面直角坐标系中，描出以表中每组对应值为坐标的点. (3) 这些点在一条直线上吗? 若在，请用直尺画出这条直线：若不在，则用透明直尺的边缘在这些点之间移动，画出一条与各点都比较接近的直线. (4) 求出这条直线所对应的函数表达式.(5) 根据所得到的函数表达式，求： ① T ＝ 100℃时，F的值； ② F ＝ 58℉时，T的值.本课结束This lesson is overTHANKS!