青岛版数学九上1.1 相似多边形 （课件PPT）

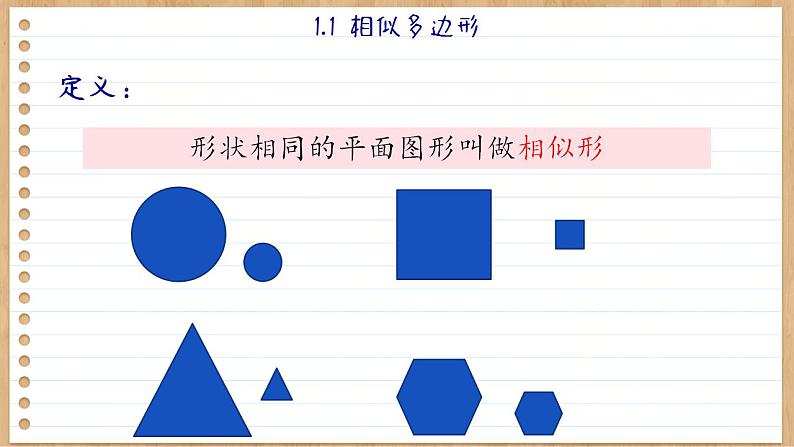
第1章 图形的相似1 . 1 相似多边形1. 从生活中形状相同的图形的实例中认识图形的相 似，理解相似图形的概念；2. 理解相似图形的性质和判定. 五星红旗是中华人民共和国的国旗.国旗上的左上角有五颗五角星.这五颗五角星的形状相同吗?大小相等吗?定义：形状相同的平面图形叫做相似形 在现实生活中，你还见过形状相同但大小未必相等的图形吗?全等和相似有什么关系呢？大小 不一定 相等两个全等形也是相似形.两个相似形未必是全等形.下列图形中，能确定相似的有( )A.两个半径不相等的圆； B.所有的等边三角形；C.所有的等腰三角形； D.所有的正方形；E.所有的等腰梯形； F.所有的正六边形.想一想A B D F 小莹在电脑上任意画出一个四边形ABCD(①)，并将它按原大复制下来，得到四边形 A′B′C′D′ (②).   (1) 观察得到的四个四边形，你发现它们的形状和大小有什么特征?它们是相似形吗? 形状相同是对相似形的一种描述，能利用两个相似多边形的各角之间及各边之间的数量关系表述它们形状相同的特征吗?  (3) 观察图1①和④，四边形ABCD与四边形A′′′B′′′C′′′D′′′相应的各角及相应的各边分别具有怎样的数量关系?图③和图④呢? 由上面的探究过程，我们发现：把四边形ABCD 复制、放大或缩小后，所得到的四边形与原来的四边形相似，它们的各个角对应相等，各边对应成比例.反过来，如果一个四边形与四边形 ABCD 的各角对应相等，并且各边对应成比例，那么这个四边形与四边形 ABCD形状相同，也就是说，这个四边形与四边形ABCD相似.由此，可以给出相似多边形的定义：相似多边形的定义: 两个边数相同的多边形，如果一个多边形的各个角与另一个多边形的各个角对应相等，各边对应成比例，那么这两个多边形叫做相似多边形. 相似通常用符号“∽”表示，读作“相似于”，那么四边形ABCD和四边形A′B′C′D′ 相似， 记作四边形ABCD∽四边形A′B′C′D′， 读作：四边形ABCD相似于四边形A′B′C′D′. (1)两个大小不等的矩形是相似的 ( )(2)一个正方形与一个平行四边形相似 ( )(3)所有的正六边形都相似 ( )(4)两个大小不等的菱形相似( )(5)各角对应相等菱形都是相似形( )判断对错并说明理由:✘✘✔✘✔下面两个矩形相似吗？6834长：长＝宽：宽想一想如果两个多边形所有的对应角相等，能相似吗？如果两个多边形所有的对应边成比例，能相似吗？如果不能举出反例。拓 展 提 高 如图，矩形的草坪长20m，宽10m，沿草坪四周外围有1m的环行小路，小路的内外边缘所成的矩形相似吗？例 1如图1-3，已知四边形AEFD~四边形EBCF. (1) 写出它们相等的角及对应边的比例式；  (2) 若AD＝3，EF＝4，求 BC的长.  由两个多边形的各个角分别相等，能断定它们相似吗?由两个多边形的边对应成比例，能断定它们相似吗?如果不能，请分别举出反例；如果能，说明你的理由.漫谈相似形 我们知道，形状相同的平面图形叫做相似形，形状相同且大小相等的图形叫做全等形.因此，全等形是相似形的特殊情况.两个全等多边形是相似比为1的相似多边形. 人类对相似形的研究和应用，有着悠久的历史. 古希腊数学家泰勒斯 (Thalcs，约公元前 625公元前 547) 是希腊几何学的先驱，早于欧几里得约 300 年，他已开始了对全等三角形和相似三角形的研究. 在他提出的为数不多的几何命题中，就有“两角及其夹边分别相等的两个三角形全等”，并根据相似三角形的原理，利用金字塔的塔高与垂直于地面的木杆的杆高之比等于它们的影长之比，测量出了埃及金字塔的高度. 欧几里得的《原本》中，在系统地建立了与全等形有关的知识体系后，专门有两卷(第V卷和第VI卷)研究了比例论和相似图形. 1679年，德国数学家莱布尼兹 (Leibniz，1646—1716)在研究图形的相似问题时，产生了一个奇妙的想法，他把拉丁字母S横过来，把相似符号写成“~”，用“·”表示全等.后人在此基础上，创造了全等符号“'”，其中上面的“~”表示两个图形相似，下面的“=”表示两个图形的大小相等，这充分反映了两个全等形形状相同、大小相等的本质. 正因为相似符号“~”和全等符号“≌”具有直观、简便等优点，所以这两个符号被数学界沿用至今. 1. 三角形与四边形能相似吗? 等边三角形与直角三角形能相似吗?为什么?三角形与四边形不能相似，因为边数不同。等边三角形与直角三角形不能相似，因为它们的角不能都相等 2. 如图，△ABC~△DFE，点A与点D，点B与点F是对应顶点.请写出它们的对应角、对应边以及对应边之间的比例式.1. 相似多边形的概念 两个边数相同的多边形，如果一个多边形的各个角与另一个多边形的各个角对应相等、各边对应成比例那么这两个多边形叫做相似多边形.2. 相似比的概念相似多边形对应边的比叫做相似比。3. 两个多边形相似的表示方法∽相似多边形的对应角相等，对应边成比例.4、 相似多边形的性质习题 1.1 1. 如果五边形ABCDE ~ 五边形A′B′C′D′E′，且五边形ABCDE与A′B′C′D′E′的相似比为k1，五边形A′B′C′D′E′与ABCDE的相似比为k2，那么k1与k2满足怎样的数量关系?k1 × k2＝12. 如图，已知△DEA~△BCA， (1) BC//DE 吗?为什么?∵△DEA∽△BCA∴∠E＝∠C∴BC//DE(2) 如果BC＝3.6，ED＝2.4，AE＝5，求AC的长. 3. 如图，四边形ABCD~四边形PQRS，BC＝8，QR＝10，PS＝6，∠B＝64°.求： (1) ∠Q的度数；∵四边形ABCD∽四边形PQRS∴∠Q＝∠B＝64° (2) AD的长； (3) 求四边形ABCD与四边形PQRS的相似比.  4. 如图，△BEA~△BAD，写出图中所有相等的角和成比例线段的比例式.  5. 已知△ABC ∽ △DEF，如果BC＝3，CA＝4，AB＝6，△DEF的最短边长为2.求： (1) △DEF各边的长；∵△ABC ∽ △DEF，BC ＝ 3， CA ＝ 4，AB ＝ 6， △DEF的最短边长为2， (2) △ABC与△DEF的相似比. △ABC与△DEF的相似比为： BC∶EF ＝ 3∶2本课结束This lesson is overTHANKS!