






还剩27页未读,
继续阅读
所属成套资源:青岛版九年级数学上册课件PPT全套
成套系列资料,整套一键下载
青岛版数学九上2.1 锐角三角比 (课件PPT)
展开
第2章
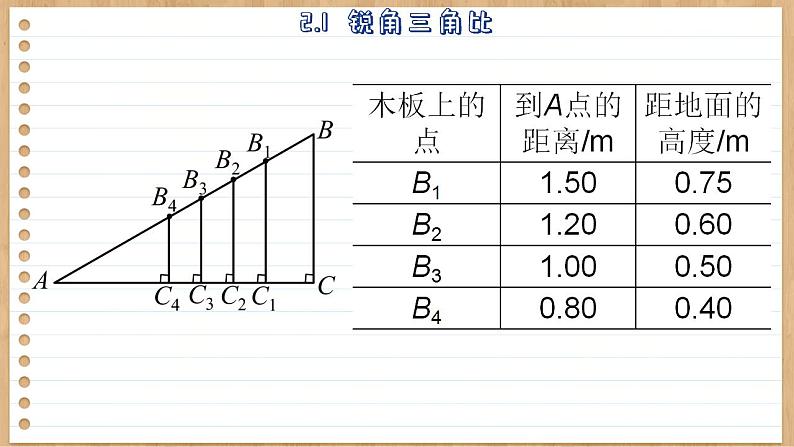
解直角三角形2 . 1 锐角三角比1. 经历锐角三角比的概念的探究.2. 正确理解三角比符号的含义,掌握锐角三角比的 表示方法. 3. 能根据定义求锐角的三角比. (1)有一块长2.00 m的平滑木板AB,小亮将它的一端B架高1m,另一端A放在平地上(图2-1),在木板上分别取点 B1,B2,B3,B4,分别量得它们到A点的距离 AB1,AB2,AB3,AB4,以及它们距地面的高度 B1C1,B2C2,B3C3,B4C4,数据如下表所示: 无关 对于确定的锐角A来说,比值k与点B在AB边上的位置无关,只与锐角A的大小有关.加油站 我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA,即 把锐角A的对边与邻边的比叫做∠A的正切 (tangent),记作tan A,即 锐角A的正弦、余弦、正切统称锐角A的三角比. 小资料 在图中,把∠A的对边记作a,∠B的对边记作b,∠C的对边记作c,你能分别用a,b,c表示∠A和∠B的正弦、余弦和正切吗?例 1 如图,在Rt△ABC中∠C=90°,a=2,b=4. 求∠A的正弦、余弦、正切的值. 1. 如果Rt△ABC ∽ Rt△A′B′C′,∠C = ∠C′ = 90°, sinA 等于sinA′ 吗? 为什么? cosA 与cosA′ 呢?2. 如图,在Rt△ABC中,∠C=90°,c=3,a=2, 求∠A的正弦、余弦、正切的值.习题 2.1 2. 在Rt△ABC中,∠C=90°,AB=2AC,求cosB 和 tanA 的值. 4. 如图,在Rt△ABC中,∠C=90°,AC=4,点D,E 在BC上,BD=5,DE=2,EC=3. 设∠ABC=α ,∠ADC= β ,∠AEC= γ , 求tanα ,cosβ ,sinγ 的值. 6. 已知等腰三角形中,两边的长分别为 10 cm和16 cm, 求它的底角的正弦、余弦和正切的值.本课结束This lesson is overTHANKS!
相关资料
更多









