青岛版九年级上册3.5 三角形的内切圆教学ppt课件

这是一份青岛版九年级上册3.5 三角形的内切圆教学ppt课件，共32页。PPT课件主要包含了习题35等内容，欢迎下载使用。

3 . 5 三角形的内切圆
掌握三角形内切圆的概念；会画三角形的内切圆；会处理与三角形内切圆相关的题目.
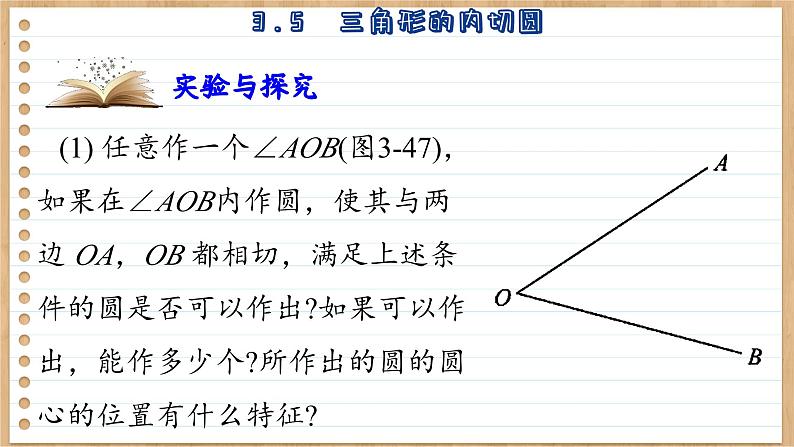
(1) 任意作一个∠AOB(图3-47)，如果在∠AOB内作圆，使其与两边 OA，OB 都相切，满足上述条件的圆是否可以作出?如果可以作出，能作多少个?所作出的圆的圆心的位置有什么特征?
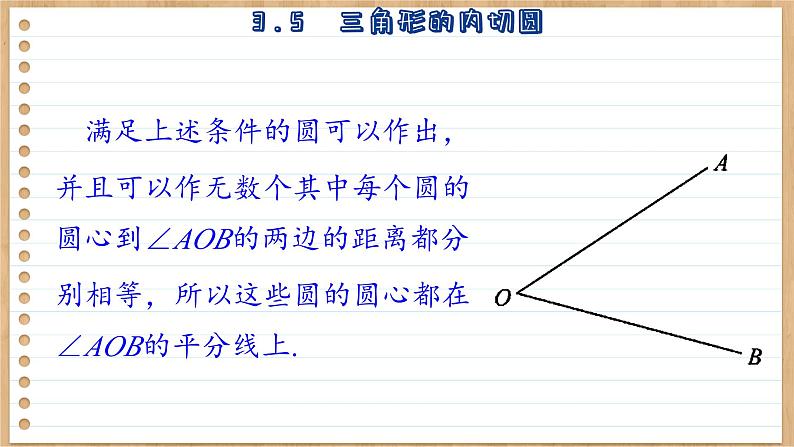
满足上述条件的圆可以作出，并且可以作无数个其中每个圆的圆心到∠AOB的两边的距离都分别相等，所以这些圆的圆心都在 ∠AOB的平分线上.
(2) 任意作一个△ABC，如果在△ABC内作圆，使其与各边都相切，满足上述条件的圆是否可以作出? 如果可以作出，能作多少个?所作出的圆的圆心的位置有什么特征?
只要能在△ABC 内找出一点，使它到各边的距离都相等，问题就可以解决了.
(3) 怎样用尺规作一个圆，使它与△ABC的各边都相切呢?
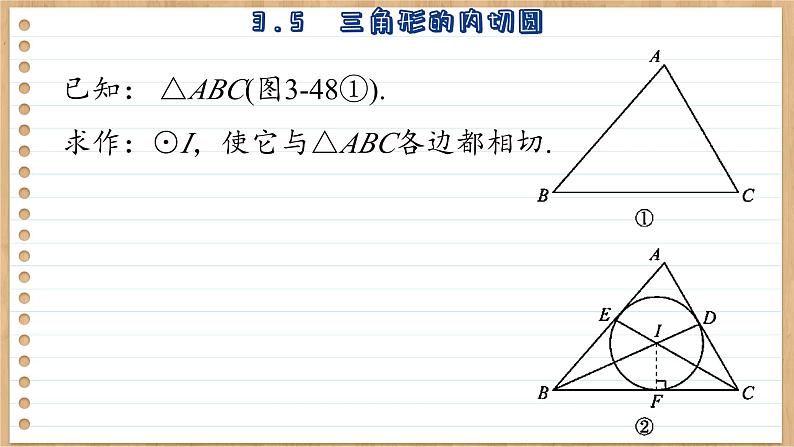
已知： △ABC(图3-48①).求作：⊙I，使它与△ABC各边都相切.
1. 作∠B，∠C的平分线BD，CE，BD与CE相交于点I；2. 过点I作 IF⊥BC，垂足为点F；3. 以I为圆心，IF为半径作圆. ⊙I 就是所求作的圆.
(4) 你能说出上面作图的道理吗?与三角形各边都相切的圆有几个?
由作法可知，与三角形的各边都相切的圆能作并且只能作出一个.
三角形的内心是三角形的三条角平分线的交点，它到三角形各边的距离相等. 任何一个三角形都有且只有一个内心，三角形的内心在三角形的内部.
与三角形各边都相切的圆叫做三角形的内切圆 ，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形.
如图3-49，在△ABC中，∠A＝68°，点I是内心. 求∠BIC的度数.
(1) 已知△ABC的三边长分别为a，b，c，它的内切圆半径为r. 求△ABC的面积.
如图(1)所示，作△ABC 的内切圆，内心为点 O，E，G，F 分别为切点,连接 OE，OG，OF，OA，OB，OC. 设AB＝c，AC＝b，BC＝a，内切圆半径为r.
(2)已知Rt△ABC的两条直角边AC，BC的长分别为b，a. 求它的内切圆半径.
1. 如图，分别作出 Rt△ABC与钝角三角形DEF的内切圆.
2. 在△ABC中，∠A＝40°，∠B＝70°点I是△ABC的内心. 求∠AIB，∠BIC和∠AIC的度数.
1. 选择题： 如图，△ABC的内切圆 O与各边分别相切于点D，E，F，则点O是△DEF的 ( ). (A)三条中线的交点 (B) 三条高的交点 (C) 三条角平分线的交点 (D)三条边的垂直平分线的交点
2. 求边长为a的等边三角形的内切圆的半径.
解：如图所示，等边三角形ABC 的边长为 a，⊙O为△ABC 的内切圆，切点分别为 D，E，F，连接 OB，OC，OD.
3. 在Rt△ABC中，∠C＝90°，⊙O是它的内切圆，⊙O与边BC，CA分别切于D，E两点. 求证：四边形ODCE是正方形.
*5. 如图，⊙O内切于△ABC，切点分别是D，E，F，AB ＝ 9，BC＝8，CA＝7. 求AD、BE、CF的长.
6. 如图， ⊙O是△ABC的外接圆，点I是△ABC的内心，延长AI交BC于点E，交⊙O于点D，连接BD，DC，BI. 求证：DB＝DC＝DI.