2023年浙江省温州市鹿城区绣山中学中考数学二模试卷

这是一份2023年浙江省温州市鹿城区绣山中学中考数学二模试卷，共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023年浙江省温州市鹿城区绣山中学中考数学二模试卷
第I卷（选择题）
一、选择题（本大题共10小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）
1. 在4，−2，0，13四个数中，最小的为(    )
A. 4 B. −2 C. 0 D. 13
2. 2023年2月10日，神舟十五号航天员乘组圆满完成了首次出舱任务，据了解，这艘飞船的时速为每小时28000千米，28000千米用科学记数法表示应为(    )
A. 0.28×105千米 B. 2.8×103千米 C. 2.8×104千米 D. 28×103千米
3. 下列各图形中，经过折叠能围成一个立方体的为(    )
A. B. C. D.
4. 不等式3x−20)个单位后过点(5,2)，则m的值为(    )
A. 2 B. 3 C. 4 D. 5
10. 如图是由四个全等的直角三角形和一个小正方形EFGH组成，恰好拼成一个大正方形ABCD，小正方形EFGH的对角线FH向两边延长，分别交边AB于点M，交边CD于点N.若E是AH的中点，则MNAB的值为(    )
A. 3 35
B. 103
C. 52
D. 2 105
第II卷（非选择题）
二、填空题（本大题共6小题，共30.0分）
11. 分解因式：2m2−8=          ．
12. 一只不透明的袋子里装有9个只有颜色不同的球，其中有3个黑球，4个白球和2个红球，搅匀后随机摸出一个球，是白球的概率为______ ．
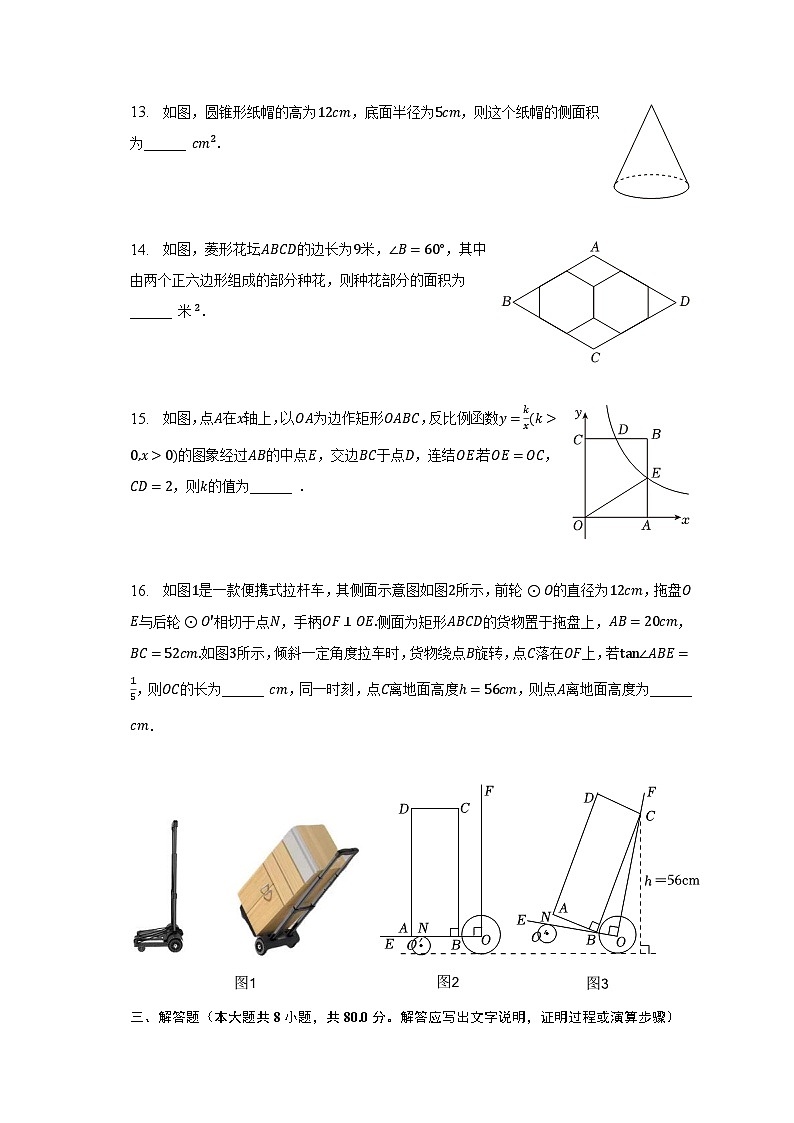
13. 如图，圆锥形纸帽的高为12cm，底面半径为5cm，则这个纸帽的侧面积为______ cm2．


14. 如图，菱形花坛ABCD的边长为9米，∠B=60°，其中由两个正六边形组成的部分种花，则种花部分的面积为______ 米 2．


15. 如图，点A在x轴上，以OA为边作矩形OABC，反比例函数y=kx(k>0,x>0)的图象经过AB的中点E，交边BC于点D，连结OE.若OE=OC，CD=2，则k的值为______ ．


16. 如图1是一款便携式拉杆车，其侧面示意图如图2所示，前轮⊙O的直径为12cm，拖盘OE与后轮⊙O′相切于点N，手柄OF⊥OE.侧面为矩形ABCD的货物置于拖盘上，AB=20cm，BC=52cm.如图3所示，倾斜一定角度拉车时，货物绕点B旋转，点C落在OF上，若tan∠ABE=15，则OC的长为______ cm，同一时刻，点C离地面高度h=56cm，则点A离地面高度为______ cm．


三、解答题（本大题共8小题，共80.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题10.0分)
(1)计算：(2− 3)0+2−2−2sin30°；
(2)解方程：x2−2x−8=0．
18. (本小题8.0分)
如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，连结BD，CE．
(1)求证：△ABD≌△ACE．
(2)若∠BCE−∠ABC=15°，求∠ABD的度数．

19. (本小题8.0分)
质量检测部门对甲、乙两家公司销售的某电子产品的使用寿命进行跟踪调查，均取10件，统计结果如下(单位：年)：
(1)分别求出这两组数据的平均数．
(2)如果你是甲公司的推销员，请你结合相关统计量及折线统计图，对本公司的产品进行推销．

20. (本小题8.0分)
如图在6×6的方格纸ABCD中，线段PQ的端点均在格点上，请按要求在四边形ABCD的边上画格点M，N．
(1)在图1中作线段MN，使得PQ平分MN．
(2)在图2中作四边形PMNQ，且PM= 2NQ．


21. (本小题10.0分)
如图，在△ABC中，AD⊥BC于点D，E，F分别为AB，AC的中点，G为边BC上一点，∠EGB=∠FDC，连结EF．
(1)求证：四边形EFCG是平行四边形．
(2)若tanB=45，tanC=2，BC=14，求GD的长．

22. (本小题10.0分)
已知点A(x1,y1)，B(x2,y2)，C(4,1)在二次函数y=a(x−2)2+3的图象上，且x2−x1=6．
(1)求该二次函数的表达式．
(2)已知点A，B在对称轴的异侧，当x1≤x≤x2时，二次函数的最大值与最小值的差为5，设x1，x2的最小值分别为m，n，求m+n的值．
23. (本小题12.0分)
根据以下素材，探索完成任务．
探究遮阳伞下的影子长度

素材1
图1是某款自动旋转遮阳伞，伞面完全张开时张角呈180°，图2是其侧面示意图.已知支架AB长为2.5米，且垂直于地面BC，悬托架AE=DE=0.5米，点E固定在伞面上，且伞面直径DF是DE的4倍.当伞面完全张开时，点D，E，F始终共线.为实现遮阳效果最佳，伞面装有接收器可以根据太阳光线的角度变化，自动调整手柄D沿着AB移动，以保证太阳光线与DF始终垂直．

素材2
某地区某天下午不同时间的太阳高度角α(太阳光线与地面的夹角)参照表：
时刻
12点
13点
14点
15点
16点
17点
太阳高度(度)
90
75
60
45
30
15
参考数据： 3≈1.7, 2≈1.4．


素材3
小明坐在露营椅上的高度(头顶到地面的距离)约为1米，如图2，小明坐的位置记为点Q．


问题解决





任务1
确定影子长度
某一时刻测得BD=1.7米.请求出此时影子GH的长度





任务2
判断是否照射到
这天14点，小明坐在离支架3米处的Q点，请判断此时小明是否会被太阳光照射到？





任务3
探究合理范围
小明打算在这天14：00−15：00露营休息，为保证小明全程不被太阳光照射到，请计算BQ的取值范围．

24. (本小题14.0分)
如图，在圆内接四边形ABCD中，AD，BC的延长线交于点E，连结BO并延长交AD于点G，连结BD.已知BD=AB，∠CDE=3∠CBD，DE=154，BO=5．
(1)求证：∠GBD=∠CBD．
(2)求OG与GD的长．
(3)F是BO中点，动点P在FG上从点F向终点G匀速运动，同时动点Q在AE上从点E向终点A匀速运动.当点Q在点D处时，点P在点O处，设QE=x，PG=y．
①求y关于x的表达式．
②连结PQ，当直线PQ与△BCD的某一边所在的直线垂直时，记垂足为点M，求QM的值．


答案和解析

1.【答案】B 
【解析】解：∵−2