初中北师大版第三章 整式及其加减3.5 探索与表达规律课后作业题

这是一份初中北师大版第三章 整式及其加减3.5 探索与表达规律课后作业题，共9页。试卷主要包含了5 探索与表达规律》课时练习，《庄子•天下篇》中写道等内容，欢迎下载使用。

2023年北师大版数学七年级上册
《3.5 探索与表达规律》课时练习
一 、选择题
1.如图，用黑白两种颜色的纸片，按黑色纸片数逐渐增加1的规律拼成下列图案，若第n个图案中有2020个白色纸片，则n的值为( )

A.671 B.672 C.673 D.674
2.下图是一个运算程序的示意图，若开始输入x的值为125，则第2 016次输出的结果为( )

A.125 B.25 C.1 D.5
3.观察下列各式： - 2x，4x2， - 8x3，16x4， - 32x5，…则第n个式子是(　　)
A.- 2n - 1xn B.( - 2)n - 1xn C.- 2nxn D.( - 2)nxn
4.观察如图所示图形，则第n个图形中三角形的个数是(　　)

A.2n＋2 B.4n＋4 C.4n D.4n-4
5.下列图形都是按照一定规律组成，第一个图形中共有2个三角形，第二个图形中共有8个三角形，第三个图形中共有14个三角形，…，依此规律，第五个图形中三角形的个数是( )

A.22 B.24 C.26 D.28
6.下列是由一些火柴搭成的图案，图①用了5根火柴，图②用了9根火柴，图③用了13根火柴，按照这种方式摆下去，摆第n○个图案用多少根火柴( )

A.4n＋3 B.5n－1 C.4n＋1 D.5n－4
7.小明用棋子摆放图形来研究数的规律，图1中棋子围成三角形，其颗数3，6，9，12，…称为三角形数，类似地，图2中的4，8，12，16，…称为正方形数，下列数既是三角形数又是正方形数的是 ( )

A.2010 B.2012 C.2014 D.2016
8.下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12个小圆圈，…，按此规律排列，则第⑦个图形中小圆圈的个数为（ ）

A.21 B.24 C.27 D.30
二 、填空题
9.观察一组数2，5，10，17，26，37，…，则第n个数是　 　.
10.《庄子•天下篇》中写道：“一尺之棰，日取其半，万世不竭”意思是：一根一尺的木棍，如果每天截取它的一半，永远也取不完，如图.

由图易得： ＝　　 .
11.当n等于1，2，3，…时，由白色小正方形和黑色小正方形组成的图形分别如图所示，则第n个图形中白色小正方形和黑色小正方形的个数总和等于 .(用含n的代数式表示，n是正整数)

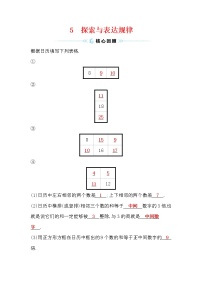
12.将从1开始的连续自然数按以下规律排列：
第1行




1




第2行



2
3
4



第3行


9
8
7
6
5


第4行

10
11
12
13
14
15
16

第5行
25
24
23
22
21
20
19
18
17
…
则2023在第 行.[
13.观察等式：1＋3＝4＝22，1＋3＋5＝9＝32 ，1＋3＋5＋7＝16＝42 ，
1＋3＋5＋7＋9＝25＝52 ，……
猜想：(1)1＋3＋5＋7…＋99 ＝ ；
(2)1＋3＋5＋7＋…＋(2n﹣1)＝ _______.
14.观察下列各式：
13＝12
13＋23＝32
13＋23＋33＝62
13＋23＋33＋43＝102
…
猜想13＋23＋33＋…＋103＝　 　.
三 、解答题
15.探究题.
用棋子摆成的“T”字形图如图所示：

(1)填写下表：
图形序号
①
②
③
④
…
⑩
每个图案中棋子个数
5
8


…

(2)写出第n个“T”字形图案中棋子的个数(用含n的代数式表示)；
(3)第20个“T”字形图案共有棋子多少个？
(4)计算前20个“T”字形图案中棋子的总个数.(提示：请你先思考下列问题：第1个图案与第20个图案中共有多少个棋子？第2个图案与第19个图案中共有多少个棋子？第3个图案与第18个图案呢？)





16.我们发现了一种“乘法就是减法”的非常有趣的运算：
①1×＝1﹣：②2×＝2﹣； ③3×＝3﹣； …
(1)请直接写出第4个等式是　　 ；
(2)试用n(n为自然数，n≥1)来表示第n个等式所反映的规律是　　 ；
(3)请说明(2)中猜想的结论是正确的．




17.察下列各式：
第1个：1×3＝3＝22﹣1
第2个：2×4＝8＝32﹣1
第3个：3×5＝15＝42﹣1
第4个：4×6＝24＝52﹣1
第5个：5×7＝35＝62﹣1
…
这些等式反映出自然数间的某种运算规律.
(1)请你根据规律写出下一个等式：　 　；
(2)设n(n≥1)表示自然数，请根据这个规律把第n个等式表示出来，并通过你所学过的整式运算知识来验证这个等式成立.
18.阅读解题：
，，， …
计算：…
＝…
＝1
＝
理解以上方法的真正含义，计算：
(1)
(2)…




19.用三角形和六边形按如图所示的规律拼图案.

(1)第4个图案中，三角形的个数有 个，六边形的个数有 个；
(2)第n(n为正整数)个图案中，三角形的个数与六边形的个数各有多少个？
(3)第2018个图案中，三角形的个数与六边形的个数各有多少个？
(4)是否存在某个符合上述规律的图案，其中有100个三角形与30个六边形？如果有，指出是第几个图案；如果没有，说明理由.








20.阅读材料：求1＋2＋22＋23＋24＋…＋22023的值.
解：设S＝1＋2＋22＋23＋24＋…＋22022＋22023，将等式两边同时乘以2得：
2S＝2＋22＋23＋24＋25＋…＋22023＋22024
将下式减去上式得2S﹣S＝22024﹣1
即S＝22024﹣1
即1＋2＋22＋23＋24＋…＋22023＝22024﹣1
请你仿照此法计算：
(1)1＋2＋22＋23＋24＋…＋210
(2)1＋3＋32＋33＋34＋…＋3n(其中n为正整数).
答案
1.C
2.D
3.D
4.C
5.C
6.C
7.D
8.B
9.答案为：n2＋1.
10.答案为：1﹣.
11.答案为：n2＋4n.
12.答案为：45.
13.答案为：502；n2.
14.答案为：552
15.解：(1)11　14　32
(2)3n＋2
(3)3n＋2＝3×20＋2＝62(个)
(4)(5＋62)×＝670(个).
16.解：等式左侧乘积的第一个因数是从1开始的连续自然数，第二个因数的分子和这个自然数相同，分母比分子大1；右侧恰是左侧两个因数的差；
(1)第4个等式：4×＝4﹣，
(2)第n个等式：n×＝n﹣，
(3)证明：n×＝，n﹣＝，
∴n×＝n﹣，
∴(2)中猜想的结论是正确的．

17.解：(1)第6个：6×8＝48＝72﹣1；故答案为：6×8＝48＝72﹣1；
(2)第n个等式为n(n＋2)＝(n＋1)2﹣1.n(n＋2)＝n2＋2n
(n＋1)2﹣1＝n2＋2n＋1﹣1＝n2＋2n，
所以n(n＋2)＝(n＋1)2﹣1.
18.解：①根据题意得：

＝
②根据题意得：
…

＝(1﹣)＝
19.解：(1)10 4;
(2)观察发现，第1个图案中有4个三角形与1个六边形，
以后每个图案都比它前一个图案增加2个三角形与1个六边形，
则第n个图案中三角形的个数为4＋2(n-1)=(2n＋2)个，六边形的个数为n.
(3)第2018个图案中，三角形的个数为2×2018＋2=4038(个)，六边形的个数为2018个.)
(4)不存在.理由如下：
假设存在这样的一个图案，其中有30个六边形，则这个图案是第30个图案，
而第30个图案中三角形的个数为2×30＋2=62≠100，
所以这样的图案不存在.
20.解：(1)设S＝1＋2＋22＋23＋24＋…＋210，
将等式两边同时乘以2得：2S＝2＋22＋23＋24＋…＋210＋211，
将下式减去上式得：2S﹣S＝211﹣1，即S＝211﹣1，
则1＋2＋22＋23＋24＋…＋210＝211﹣1；
(2)设S＝1＋3＋32＋33＋34＋…＋3n①，
两边同时乘以3得：3S＝3＋32＋33＋34＋…＋3n＋3n＋1②，
②﹣①得：3S﹣S＝3n＋1﹣1，即S＝(3n＋1﹣1)，
则1＋3＋32＋33＋34＋…＋3n＝(3n＋1﹣1).